02-prop-of-graph-and-rand-model
Properities of networks, Random Graph Model
在下面所提到的图默认是无向图。介绍了graph的四种属性
Network Properties
4 key network properties
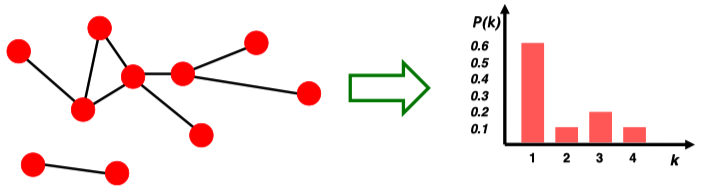
- Degree distribution \(P(k)\)
具有不同度的节点数量在所有graph node中的比例
- Paths in a graph
在图中的路径path是指节点的序列。在有向图中的path需要遵循edge的direction。
有了path就可以衡量距离distance,两个节点的distance是最短路径shortest path。
定义了distance之后,可以定义graph的直径diameter。graph的diameter是所有节点对的distance中最长的值。
- Clustering coefficient
聚类系数clustering coefficient衡量了节点的邻居之间的连接性。clustering coefficient针对的是graph中的每一个node。具体算法是计算邻居之间的边/理想中最多的领居间边的数量。 \[ C_i= \frac{2e_i}{k_i(k_i-1)} \] 其中,\(e_i\)是邻居间的边的数量,\(k_i\)是节点\(i\)的度。\(k_i(k_i-1)\)计算了所有邻居节点之间都存在一个边的上限情况。聚类系数在0-1区间。
- Connectivity
定义为最大连通单元中节点的数量。

Random Graph Model
我们可以设定一些条件,产生人造的随机graph,来促进我们对于现实graph的理解。
可以有两种random graph
- \(G_{np}\):n个node,node之间产生edge的概率是\(p\)。
- \(G_{nm}\):n个节点,随机产生\(m\)个边。
研究这两种random graph的properties。
对于\(G_{np}\):
Degree Distribution
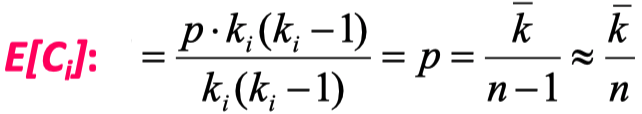
Clustering Coefficient
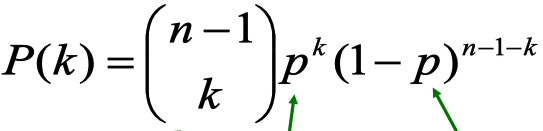
Path Length
首先定义Expansion,核心思想是随机选一个node集合,有多少的边会离开这个集合。
式子定义:

式子下面的分母表示对于一个划分来说,如果划分的S越大,节点越多,如果离开集合S的edge数量不变,那么expansion应该小;如果划分的集合S的node数量不变,那么离开S的edge数量越多,expansion越大。随机的划分S,能得到V-S,对于S和V-S都可以计算出一个expansion,离开这两个集合的edge数量一样,但是如果拿较大的集合来算的话,计算出来的expansion就会偏小。因此,总是以数量较少的集合作为考虑的点。
随机的划分集合,能得到很多的expansion,为了衡量整个graph的expansion,考虑expansion的下限,即最小的那个expansion。在这种情况下,如果graph的expansion比其它graph的expansion更大,可以理解为这个graph的expansion更大,locality更弱。
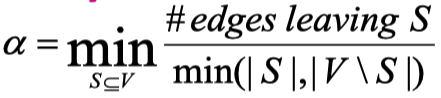
一个random graph的path length是\(O(log\ n)\)。diameter是:

也就是说对于random graph来说,随着node数量增加,diameter并不会增加很多。
Lagest Connected Components
在random graph中,随着平均degree增加,node链接到giant component的概率增加。
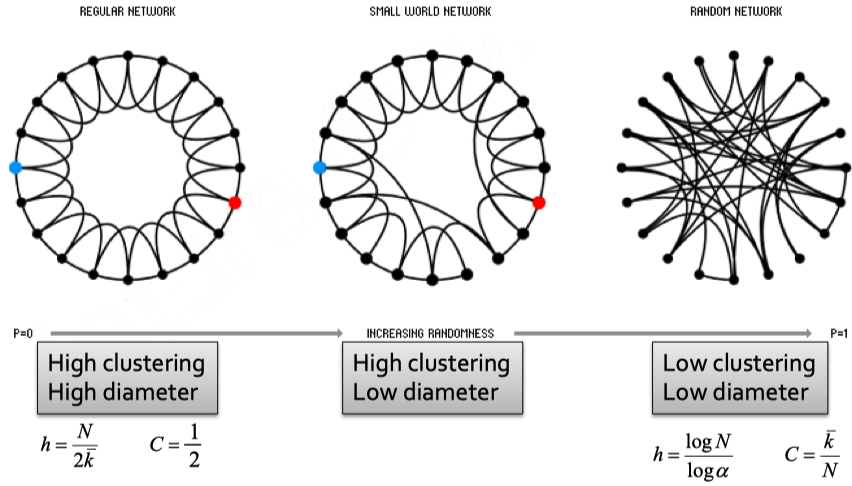
The Smallest-World Model
仔细观察下network的properties会发现,聚类系数与graph的直径似乎是两个有点冲突的属性。如果聚类系数比较高,说明一个graph的locality强,那么node与较远的node之间就比较难有直接的链接,这会造成graph的路径很大。
一个graph的diameter衡量了graph的“shortcut”,如果diameter比较小,意味着对于一个node,可以在较小的step内链接到其它node。但是直径变小的话,一个graph的locality似乎会被破坏,一个node的很多邻居之间不相连,而是有更多的edge链接到其它的node上。
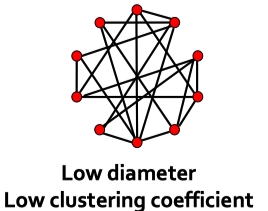
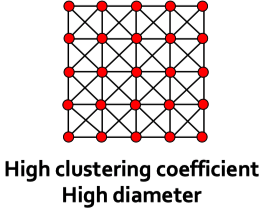
那么,是否有办法让graph同时具有high clustering和small diameter?
解决方案是the smallest-world model。1998。
核心是对于一个已经具有high clustering的graph,引入randomness,新增/删减edge来创建更多的“shortcut”。
示例图: