1-Interoduction-word-vectors
1 Introduction and Word Vectors
Human language and word meaning
human language的特征:
- 不确定性。我们尝试使用语言来描述世界,表达自己的想法,但是自己表述的语言能否被其它的人接受实际是不确定的,可能是一种概率的问题。
- ”human language is a pathetically slow network“,说话这种方式能够表达的能力是很有限的,因此在人类的交流中,实际语言是实现了一种对于信息的压缩,能够理解语言的背后是我们的大脑中已经拥有了很多先验知识。
Represent the meaning of word
Definition: meaning
- the idea that is represented by a word
在早期的NLP中,人们将不同的词word表示为独立的符号(discrete symbol),这叫做localist representation,例如one-hot编码。
这样表示的问题:
- word的数量很大,甚至可以构造出无限多的word,导致one-hot编码的dim越来越大
- 对于one hot编码来说,不同的编码之间是独立的,和正交的,无法保留word原本的含义,也无法衡量两个word之间的相似程度
如何获取一个word的meaning?
一个著名的观点是:
”You shall know a word by the company it keeps“
——J. R. Firth 1957: 11
A word’s meaning is given by the words that frequently appear close-by.
针对one hot的问题,我们尝试为每个word建立更dense vector,即使word的distributed representation,word vector。
Word2vec
借助于前面的观点,word2vec出现了。
Word2vec (Mikolov et al. 2013) is a framework for learning word vectors
核心思想:
- 一个大的语料库
- 每个word都使用固定长度的vector表示
- 选中center word,计算它周围的outside word/context word出现的概率,并且不断更新参数让这个概率最大
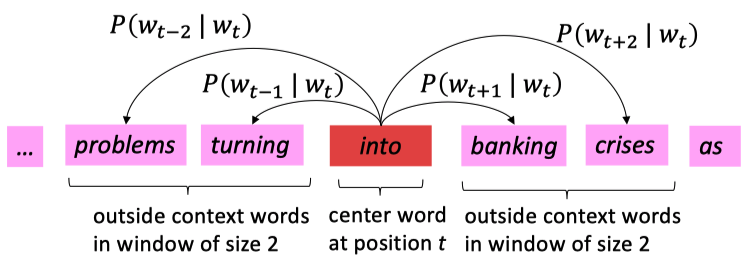
核心问题在于如何计算\(P(w_{t+j}|w_t)\)?
在word2vec中,对于每个word建立两个vector:
- \(v_w\) when word \(w\) is a center word
- \(u_w\) when word \(w\) is a context word
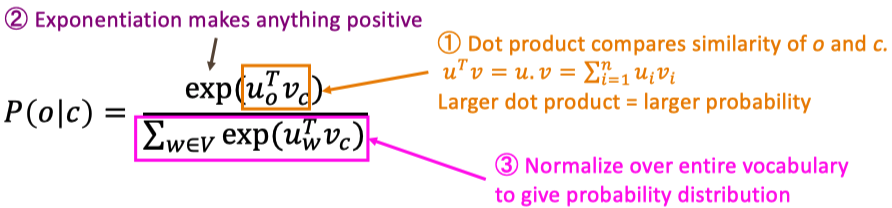
核心公式: \[ P(o|c)=\frac{\text{exp}(u_o^T v_c)}{\sum_{w\in V} \text{exp}(u_w^T v_c)} \] 解释

使用点积来衡量相似度,当我们得知了context的时候,中心词的meaning应该也能知悉,即context与center word的meaning此时应该接近。对于在语料中经常出现的word,赋予它们比较大的概率。
上面的公示实际是softmax
- soft:指对于所有的预测目标都有一个估计概率,哪怕它可能很小
- max:指softmax的输出是概率最大的值