RL/foundational_rl
深度强化学习基础概念理解与思考
深度强化学习基本概念、经典算法的理解与思考。
参考学习资料:
王树森. 深度强化学习.
李宏毅. 深度强化学习.
1. 基本概念理解
强化学习旨在强化增强模型原本就有的能力,而不是赋予新的能力。因为强化学习的优化源自于动作的奖励,然后修正。这要求模型本身就有内在基本的,可以做对正确动作的潜力。它与监督学习的区别之一在于,模型输入不是固定的,能够得到的奖励也不是固定的。在一个分类任务中,模型输入是训练数据决定的。模型训练好坏,不会改变数据输入。而强化学习每一步的输入,是由环境根据上一步模型的动作给出的新的状态。监督学习的奖励是始终根据唯一正确的ground-truth annotation来计算的,而强化学习的奖励是根据各个步的状态和动作一起决定的。
一些基本术语:

agent是一个很灵活的概念,可以是一个机械臂、机器人、虚拟人物等等,每个人的理解不一样,一般我们就认为它是一个被期望能够智能地做任务的主体。agent的大脑就是policy,policy会根据环境当前的state,决定action。有时候这两个词会互换,因为我们关注的就是如何拥有更好的虚拟大脑,实现更好的决策。
环境就是agent所处的“世界”,它可以交互的唯一。环境会根据agent决定好了action之后,从上一个状态被action转化为下一个状态。状态转移函数就发生在环境内。
奖励是我们人类鼓励的方向,判断什么动作好,什么动作不好。强化学习的奖励常常是稀疏的,因为很多动作没有当下及时反馈的好与坏。例如游戏人物随机走一步,没有好坏。但是这个好坏可能是影响到了未来。因此,奖励常常使用accumulated reward(也叫做return,强化学习任务达到终止状态,可以计算累积奖励了)。
回报return是累积未来奖励,价值value是回报的条件期望(条件是给定状态或动作)。

强化学习的学习过程与目标:
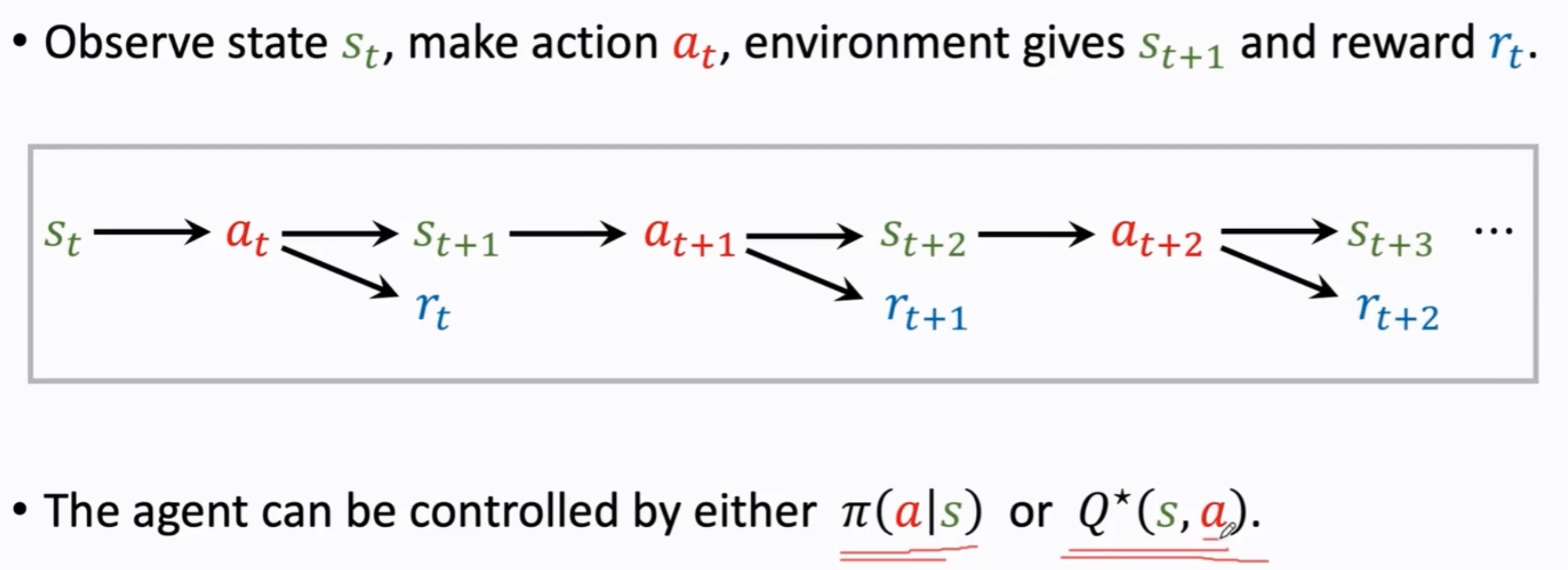
agent动作的决定可以是直接由一个policy network决定,也可以是由optimal action-value function决定。
value function有两种,state value function和action value function。state value function描述当前局面的好坏,action value function描述当前状态下采取某个动作的好坏。这里的好坏,就是指累积奖励的期望。相同state下,state value function越大,代表学习到的agent越好;相同state下,采用某个动作的action value越大,代表此时对于这个agent来说采用这个动作越好。


RL与监督学习的另一个区别就在于,强化学习的随机性更加重要,甚至就是强化学习的精华所在。强化学习的随机主要来源有两个:
- action有随机性:来源于agent,目的有两个(1)探索所有可能的动作,然后才能知道采取这个动作是好还是坏;(2)动作有随机性可能就是任务期望的一部分,比如训练一个猜拳游戏的强化学习,失去随机性意味着拥有规律(赞美混沌)。
- 状态state有随机性:来源于环境本身,一个游戏里随机刷新的小怪,小怪的动作等。状态转移函数就可能是随机,而不是固定的。
On-policy的意思是,在RL的每一轮,我们要使用agent去与环境交互,生成状态–动作-奖励-状态–动作-奖励-…的序列。然后反过来优化agent。
Off-policy的意思是,在RL的每一轮,与环境交互产生训练数据的agent,与实际优化的agent不是一个agent。

2. 价值学习Value Learning
价值学习就是学习一个critic,critic有两种,一种是判断state value,一种是判断action value。利用神经网络估计state value的方法有两种,一种是蒙特卡洛,基于采样,然后回归训练:
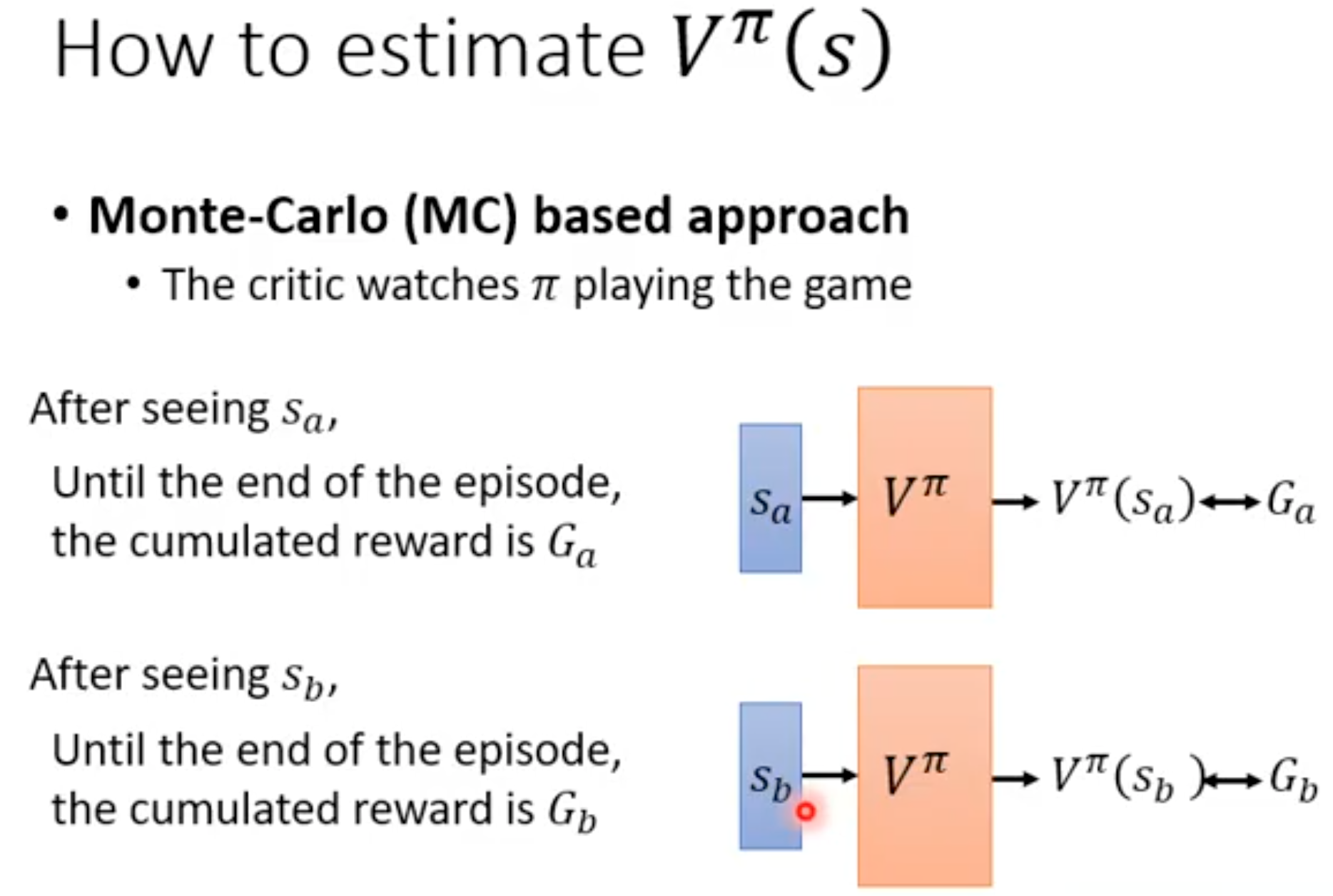
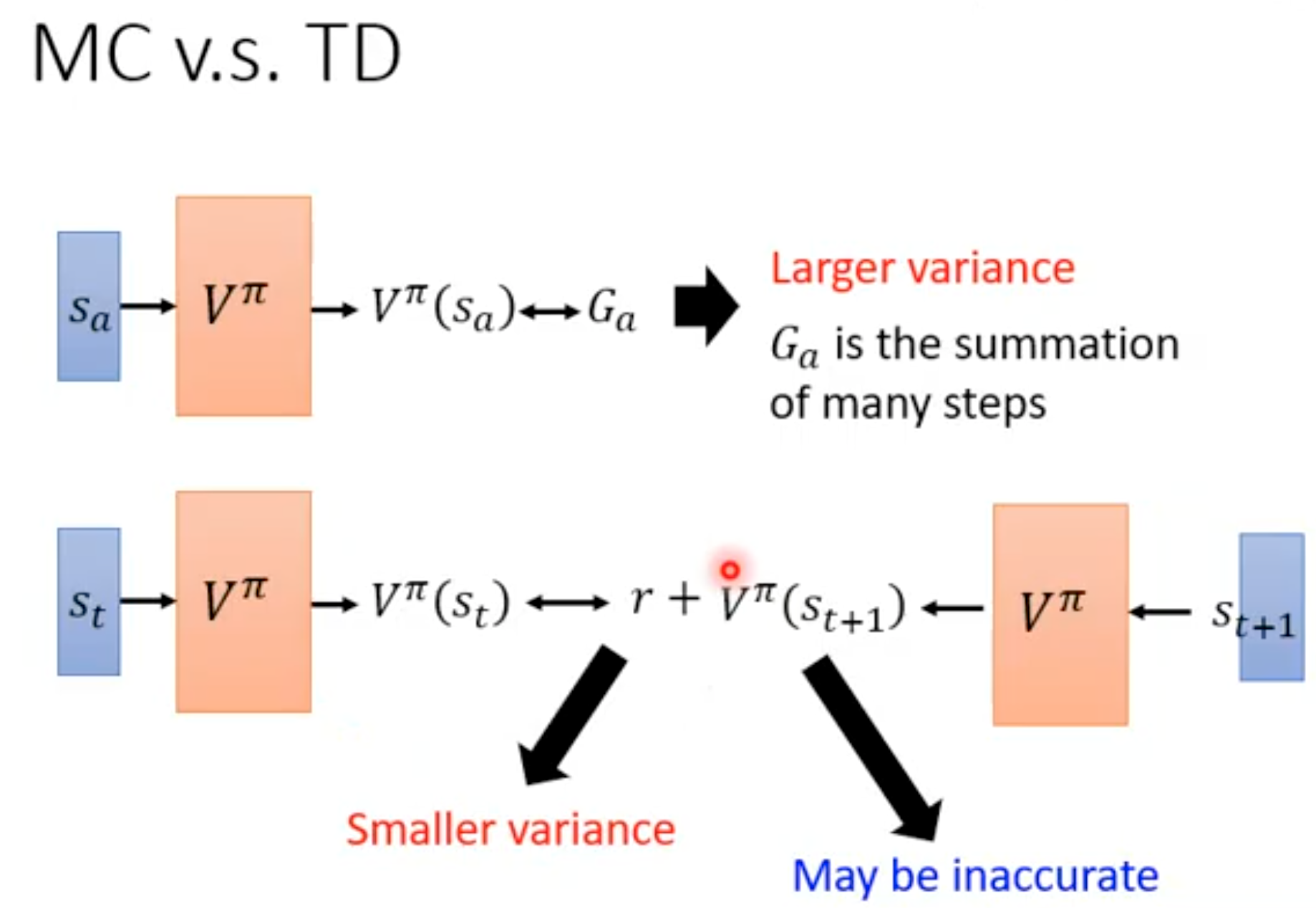
另外一种就是利用TD方法:

两种策略的对比,MC方法的方差更大,而TD方法可能估计的不准确。
Q-Learning
要通过利用action value来选择进行哪个动作,那么目的就是学习RL中的最优动作价值函数\(Q^\star(s_t,a_t)\)。最优动作价值函数存在是为了评估在无论policy function学习的好还是坏情况下,理论上能取得的最大的未来累积奖励的期望,也就是动作价值\(max_\pi Q_\pi (s_t,a_t)\)。期望奖励是某个policy在当前状态\(s_t\)采取动作\(a_t\)后,能够取得的预期未来累积奖励\(Q_\pi (s_t,a_t)=E(U_t|s_t,a_t)\)。
我们只要能够学习到最优价值函数\(Q^\star(s_t,a_t)\)就好了,这样我们只需要选择能够产生最大理论期望值的那个动作就行。但是没法真的拿到这种理论最好的函数。
所以只能估计。如何估计?利用DNN。
这个估计最优价值函数\(Q^\star(s_t,a_t)\)的DNN就叫做Q-Network。想让这个Q网络的输出和最优价值函数\(Q^\star(s_t,a_t)\)的输出一样。
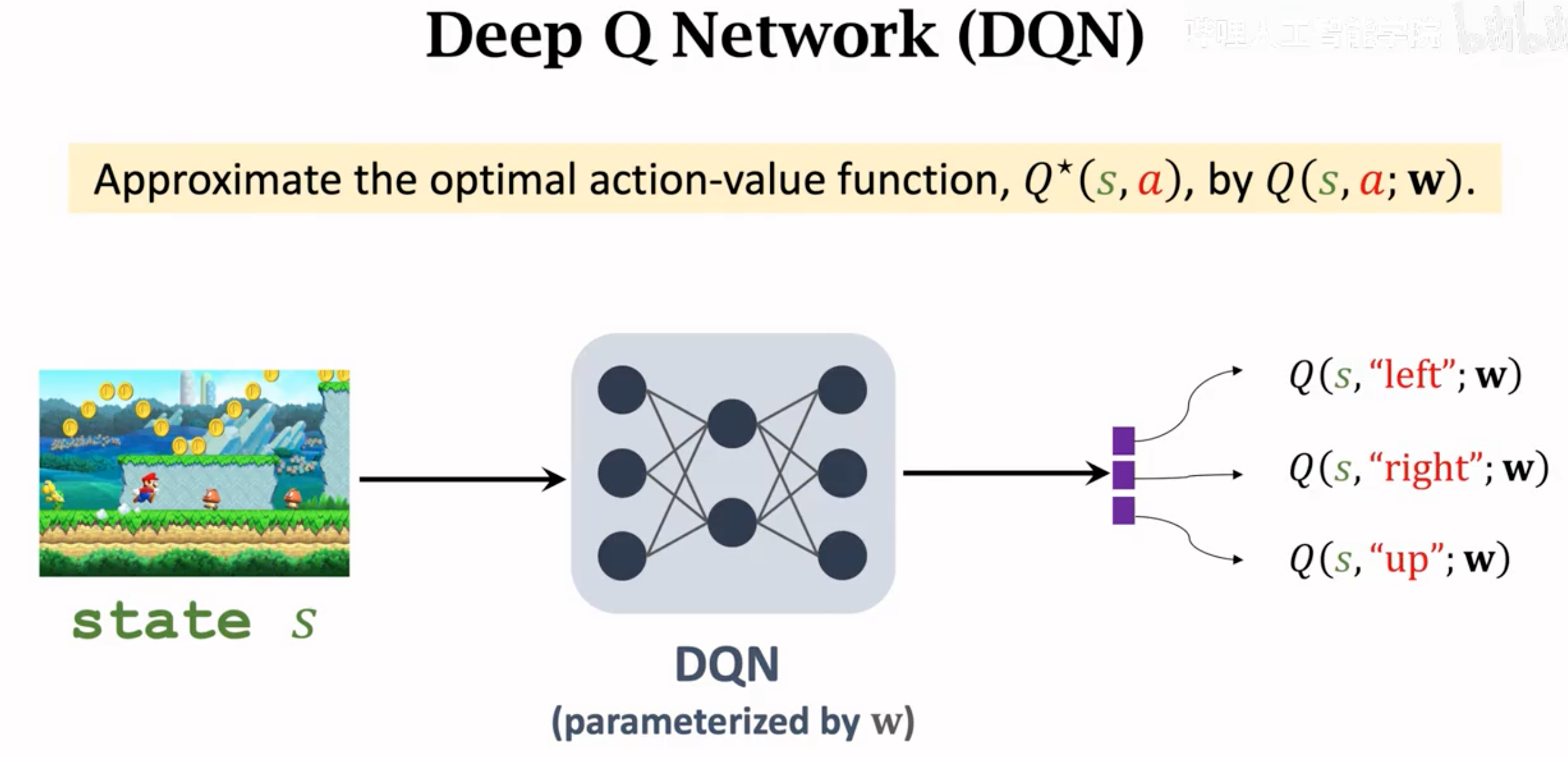
如何训练?
一个常用的学习方法是TD(temporal difference)learning。我们并不知道最优价值,没法用最优价值的绝对值作为ground-truth annotation来监督微调Q网络。但没有关系,在这种情况下,往往我们可以尝试使用其中的一些内在关联或间接的相对的规律来作为监督信号。 
对上面\(U_t\)与\(U_{t+1}\)的数学关系公式求期望: \[ E(U_t)=E(R_t)+\gamma E(U_{t+1}) \] 一个更加详细的推导:

因为我们现在得到的TD target是一个累积未来奖励的期望,很难直接求。TD target的本质是加入了观察到的奖励后对当前价值的估计。所以可以用后面小节里介绍的蒙特卡洛方法进行估计。这里蒙特卡洛方法估计相当于是仅抽样一次:
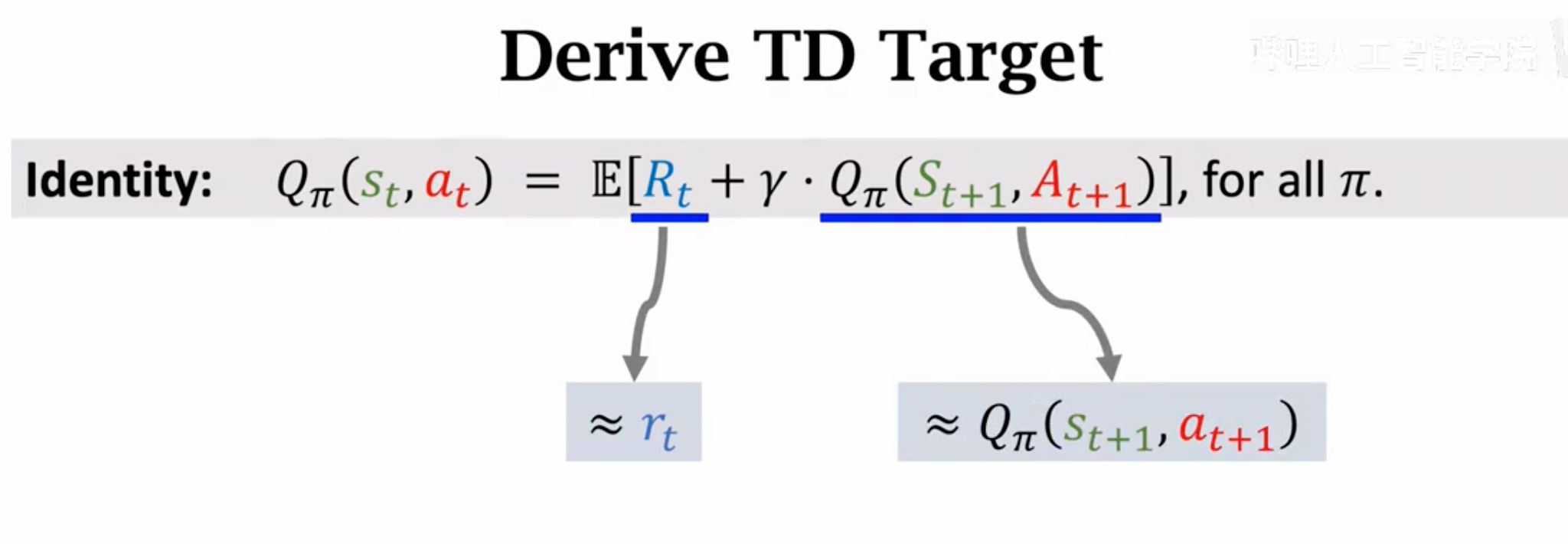
上面得到的右边两项就是所谓的TD target \(y_t\),它部分是有真实观测值\(r_t\),更加可靠,所以我们希望让左边的估计值能够逼近\(y_t\)。TD学习算法的核心都是上述推导过程,观测TD target,计算TD error,然后更新参数(可以是policy function的参数,也可以是value function的参数)。
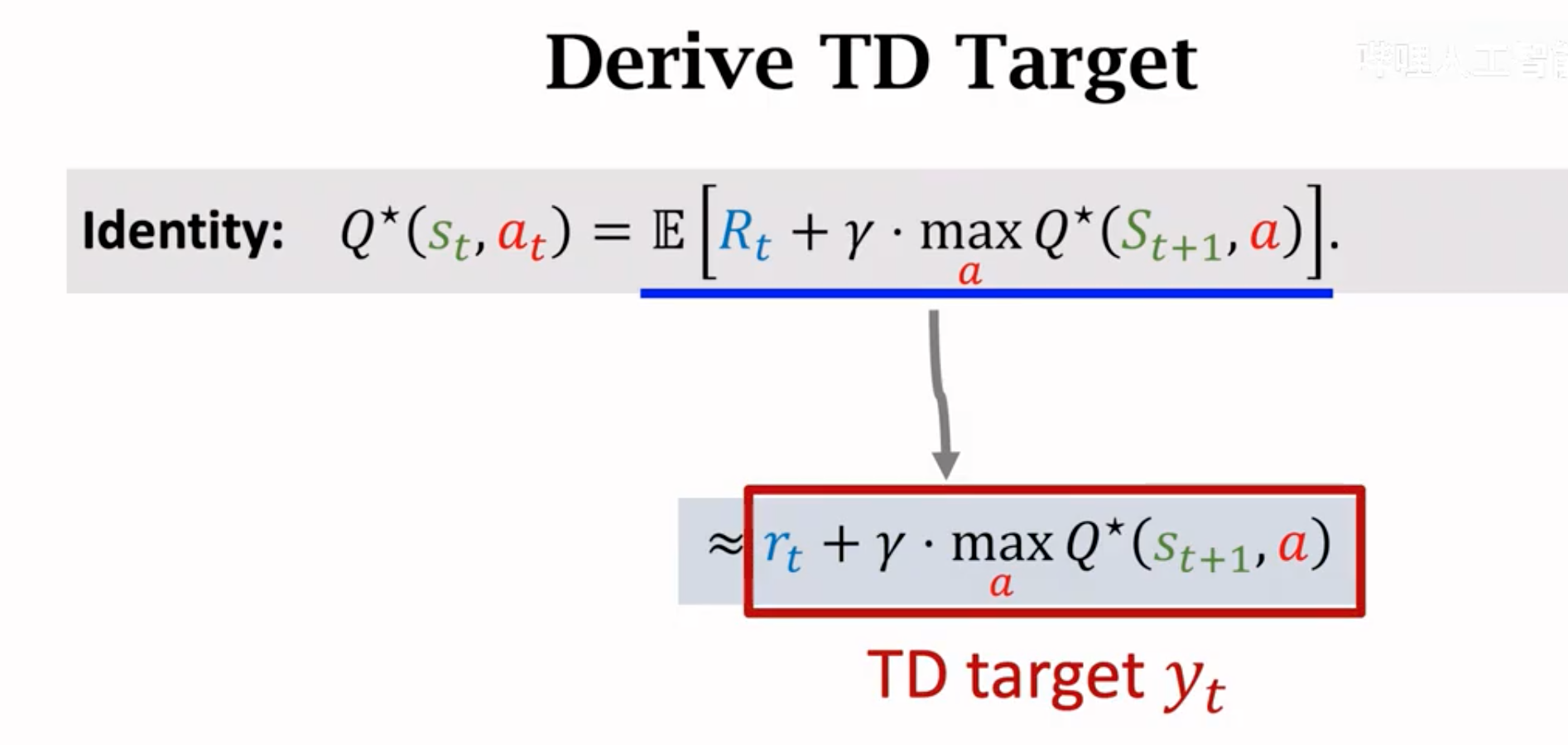
下面是利用TD算法的Q-learning算法来估计最优value function \(Q^\star(s_t,a_t)\)。首先推导最优价值函数:

对下一步的\(Q^\star(S_{t+1},A_{t+1})\)继续推导,它里面的动作\(A_{t+1}\)就是能够让下一步动作价值最大的那个动作(不再是SARSA算法的随机动作):

直接求期望很困难,所以我们还是要借助蒙特卡洛的力量来进行估计:
Q-Learing方法也有表格的形式,这里不赘述,此时不能叫做深度强化学习,而是非DNN的强化学习。

下面是使用神经网络来进行估计的版本。让我们的Q网络输出也能够满足上面的关系,也就是说:  这样我们就可以进行训练,微调Q网络(参数为\(\mathbf{w}\))了:
这样我们就可以进行训练,微调Q网络(参数为\(\mathbf{w}\))了:

一个基本的naive流程:
- 每一时刻\(t\),先使用Q网络预测动作\(a_t\)最优价值即最大理论期望\(Q(s_t,a_t;\mathbf{w_t})\)。
- 动作与环境交互,环境返回reward \(r_t\)和新的状态\(s_{t+1}\)。
- 再使用Q网络预测新的状态\(s_{t+1}\)下,采取不同动作对应的最大价值,选择价值最大的\(max_a Q(s_{t+1},a;\mathbf{w}_t)\)。
- reward \(r_t\)与\(max_a Q(s_{t+1},a;\mathbf{w}_t)\)是TD target,\(Q(s_t,a_t;\mathbf{w_t})\)应该和其相等。计算loss,最后梯度下降,更新Q网络。
注意上面的流程里,在实践中,估计TD target使用的网络参数不会和Q网络是相同的参数,这会导致训练很不稳定。一般会使用冻结的前几步的Q网络来作为target network估计TD target。这种操作也能够在一定程度上缓解Q网络的高估问题,具体在下一小节里有详细的讨论:

Exploration for DQN
由于Q-learning学习的是最优动作价值函数,每次做决策的时候是会选择价值最大的对应的动作。如果在训练的阶段也一直采用这种手段,会导致RL的exploration不充分。下面是两种简单的让DQN能够进行exploration的方法:

上面这个操作,相当于是在选择action的时候加入了noise。但是这种做法不一定是最合适的。以epsilon greedy为例,它训练出来的agent只有在训练的时候会以一定的概率突然变为随机选择选择一个action。也就是说,给定相同的state,DQN最后要决定的action概率会不一样,这种行为并不是在真正inference的时候agent会做的。为了解决这一问题,DeepMind和OpenAI都在同一年提出了noise net,在每一轮episode开始阶段,为DQN的参数加入noise,这个noise在同一个episode里保持不变,直到下一个episode才会选择出新的noise。


Experience Replay
在上面的native流程中,每一步更新一次参数,而且每个奖励都只会被使用一次。也就是说,每个产生的state transition都只使用一次就不再使用了。这带来两方面的问题:
(1)浪费之前记录的transition:

(2)每个transition用来序列地更新的时候,\(s_t\)和\(s_{t+1}\)是紧密相关的,而\(s_{t+1}\)又和\(s_{t+2}\)紧密相关。这种序列的强相关性可能对RL的学习有害:

经验重放就是保留过去的\(n\)条transition,构建一个transition buffer用来计算TD error:
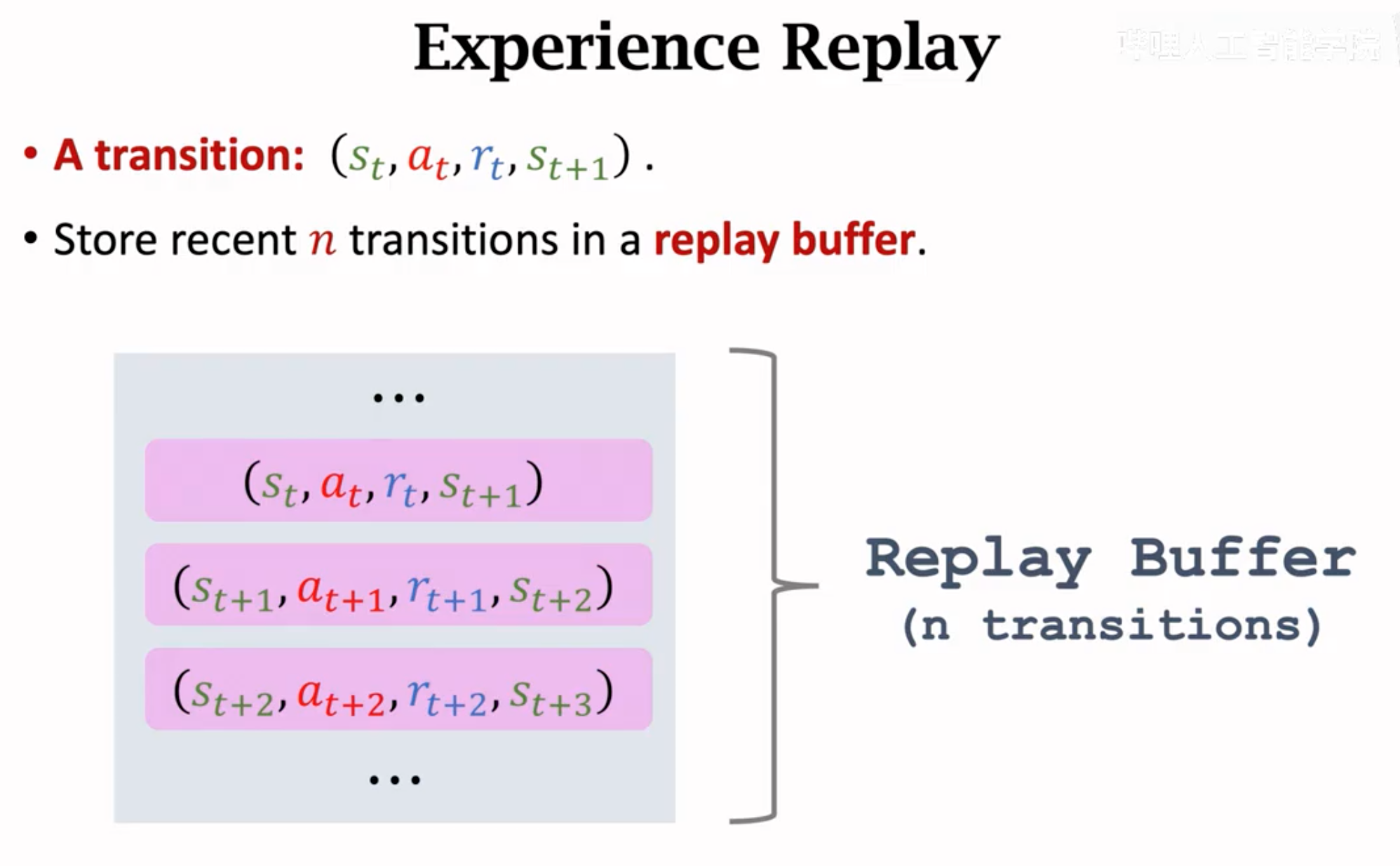
达到最大容量\(n\)时,就除去最老的那一个transition。

实践的时候,每次要更新Q网络,从experience buffer里随机找一个batch的transition,然后计算TD error \(\delta=q_t-y_t\),计算平均梯度:

DQN在2015年被提出来的时候,就是用了经验重放:

Priortized Experience Replay
在经典的经验回放中,每个transition被采样得到的概率是相等的。但是这种均匀采样不一定合理。比如在下面的实例中,右边agent在对抗boss的transition是更稀少的,也是更有可能让估计出错的情况。我们事实上应该给这种transition更高的优先级。

那么什么样的transition应该有更高优先级?可以利用TD error来估计,更容易出错的就是更优先的,也就是拥有更大的被采样概率。

之后,我们应该调整学习策略,避免这种不均匀的采样对模型训练带来的影响。使用下的策略调整不同transition对应的学习率,优先级越高的学习率越低:

如果一条transition被加入了buffer里,就给他最大优先级;如果一条transition被选中用来更新Q网络,就更新它新的TD error。

下面就是优先经验回放的基本思路:

Double DQN
这一小节讨论DQN的高估或者说过度估计问题,也就是DQN往往会让估计的TD target \(y_t\)大于期望,优化出来的Q网络对于动作价值会不均匀的高估,导致选不出来好的动作。下面是Double DQN论文中的图片:
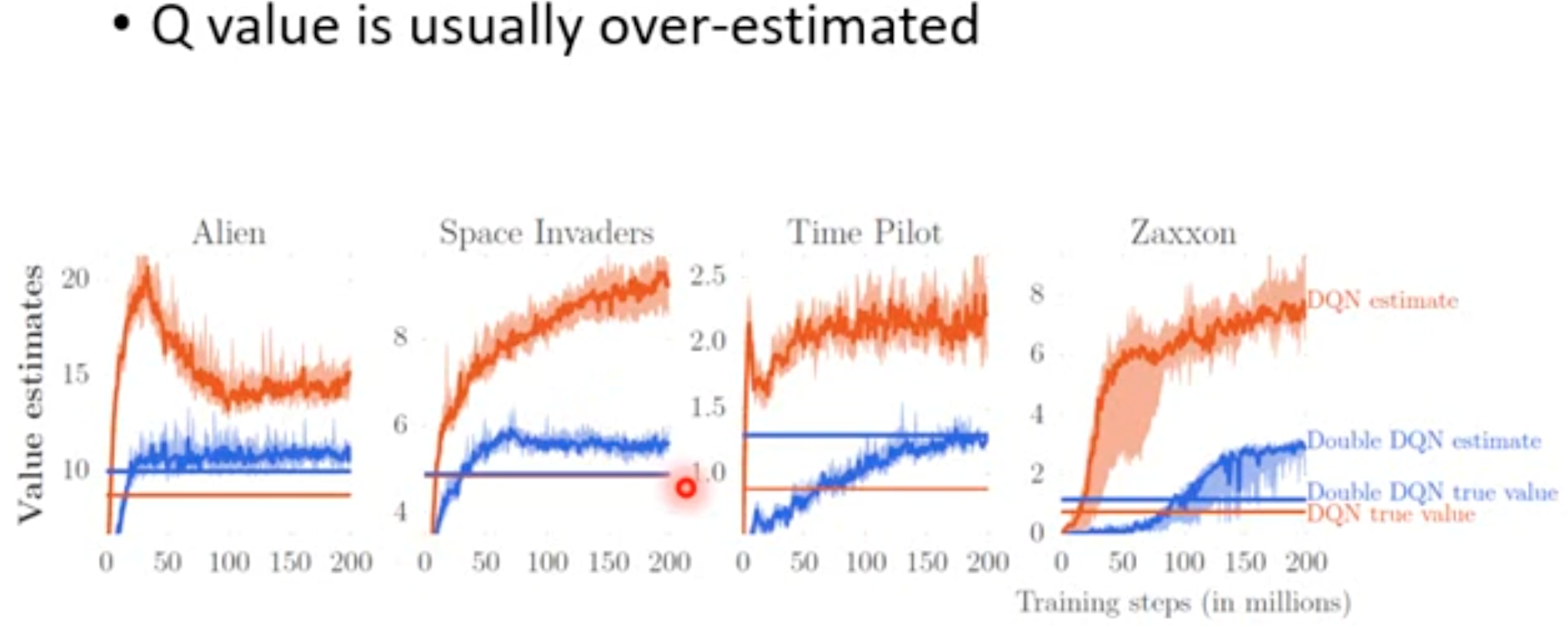
从图中可以看出来,单纯的DQN红色的曲线要远远高于实际统计的value值。这就是DQN的高估问题。
DQN希望用一个Q网络来拟合optimal action value function,需要用到下面公式: \[ Q^\star_{\pi^\star}(s_t,a_t) =E(R_t) + \gamma\ E(Q^\star_{\pi^\star}(s_{t+1},A))= E(R_t) + \gamma\ E( max_{a+1} Q^\star_{\pi^\star}(s_{t+1},a_{t+1})) \] 上述公式没有问题,但我们根本不知道真实期望,只能估计期望。为了估计期望,使用当前奖励\(r_t\)估计\(E(R_t)\),使用\(max_{a+1} Q^\star_{\pi^\star}(s_{t+1},a_{t+1};\mathbf{w})\)估计\(E(Q^\star_{\pi^\star}(s_{t+1},a_{t+1}))\)。

上述公式DQN用来计算TD target \(y_t\),然后更新Q网络参数\(\mathbf{w}\)。这样高估问题来源是两个,一个是max操作,一个是选择\(a_{t+1}\)用的还是DQN的当前步参数\(\mathbf{w}\)(这种操作叫做自举)。
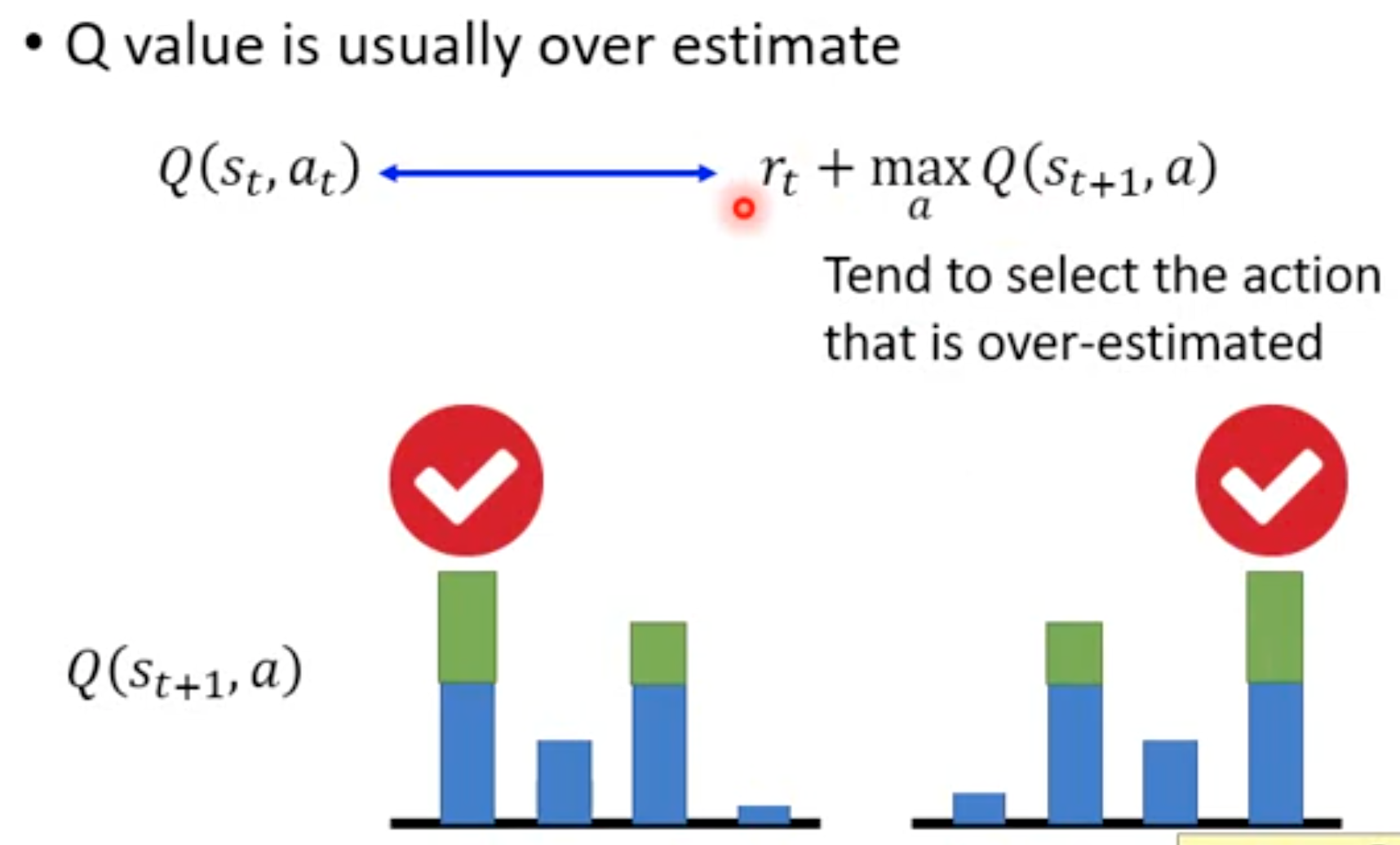
max操作带来的高估问题直观理解就是,不同的动作\(a_{t+1}\)估计的value有的可能高于真实值,有的可能低于真实值,max操作总是会喜欢选择那些被高估的。一个动作越是被高估,越会被选中。以下面的图为例:
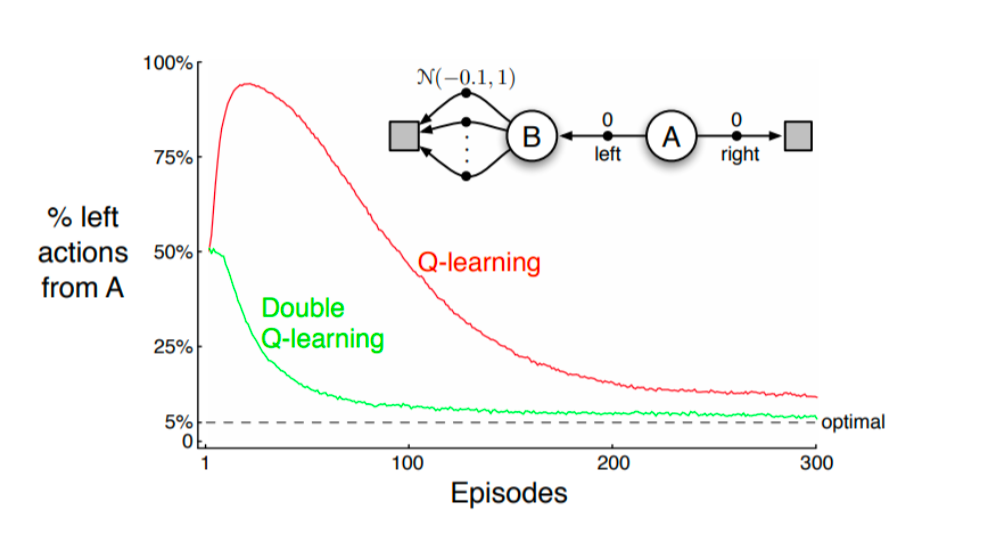
下面是关于max操作会引起高估问题的数学证明。给定一组带有随机噪音的变量(这里的变量就是我们用神经网络估计的各个动作\(a_{t+1}\)的价值,神经网络总是有噪音的),假设变量的噪音是zero-mean。从这组变量中,选择最大值出来的变量所对应的期望,往往是要大于一组变量期望的最大值的(由于噪音是zero-mean的,一组变量的期望还是和没有噪音相等)。下面是数学的解释。


使用max操作选出来的动作\(a_{t+1}\)的期望,总是比从各个动作的期望里选择最大值要大。即最大值的期望,要大于期望的最大值。
自举带来的高估问题在于高估倾向的传播,即如果Q网络参数\(\mathbf{w}\)在之前的更新里已经是训练成高估的,那么现在这一步计算TD target \(y_t\)再更新参数\(\mathbf{w}\),就会让参数\(\mathbf{w}\)更加高估。

但是高估就一定有害吗?不一定,因为如果我们对每个动作的高估程度都是一样的,比如说都是大于真实价值\(100\),那么选择出来的价值最大的动作是不变的。问题就在于,高估的程度根本不可能是一样均匀的。一个原因是,不同状态下的动作,被用来高估然后优化的次数,就是不相同的。从experience buffer中选择transition不可能均匀:

所以为了解决高估问题,有两个方法。第一种方法是使用target network缓解boostraping带来的高估问题。也就是不要用参数\(\mathbf{w}\)估计TD target \(y_t\),然后再更新参数\(\mathbf{w}\)(这个方法使得Q-Learning能够在玩ATARI游戏集合上表现出较好的效果):
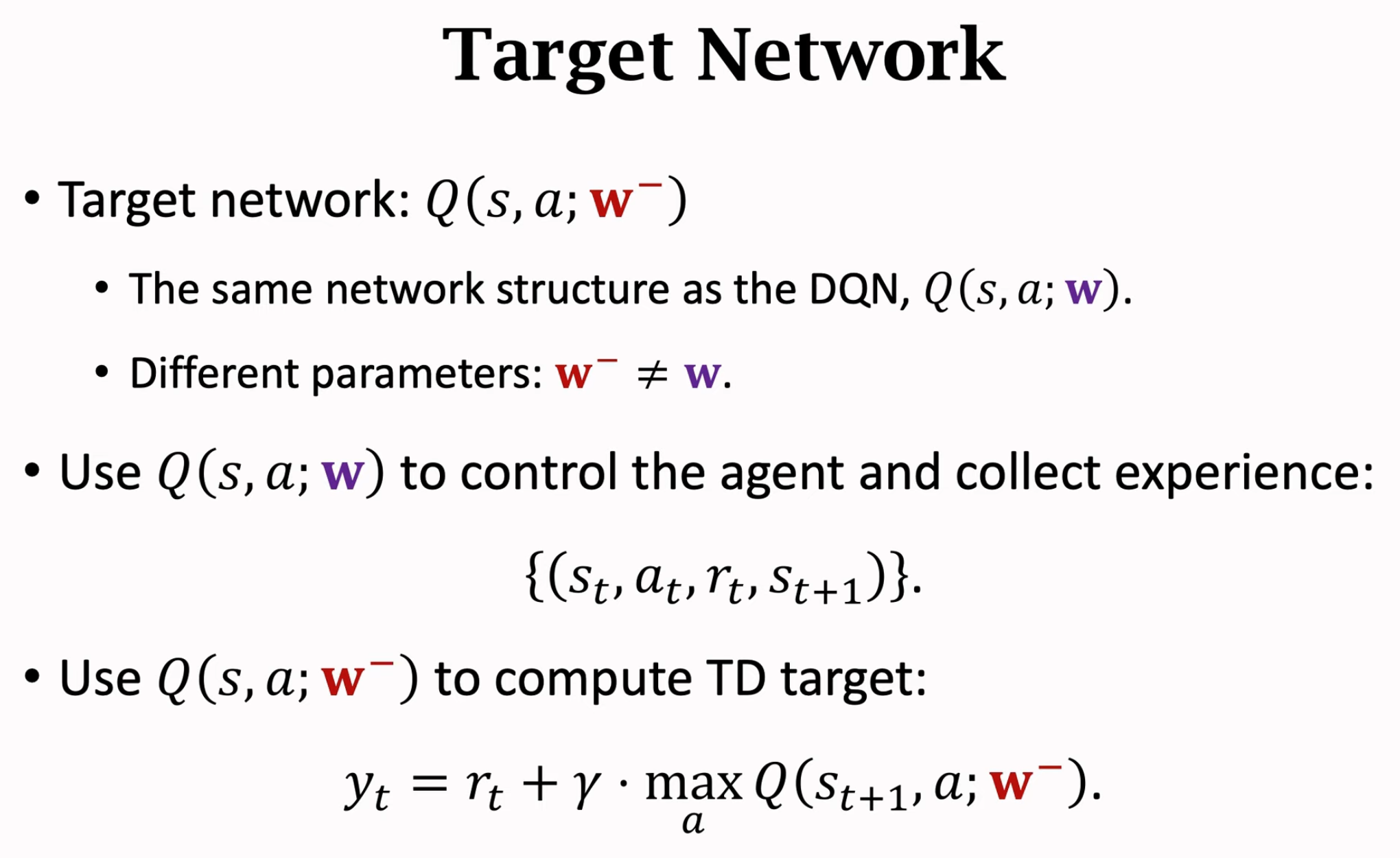
估计\(Q^\star(a_{t+1},s_{t+1})\)价值的网络是target network,它有了独立的参数\(\mathbf{w}^-\),它的参数来源实际上是冻结的之前步骤得到的参数\(\mathbf{w}\),每隔一段时间更新\(\mathbf{w}^-\):

上面的第一个方法实际上就是在Q-Learning中最后给出来的DQN算法。估计TD target的网络参数与当前待更新的Q网络参数不一样。
第二个方法是想缓解max操作带来的高估问题。试想一下,如果我们只要不选择\(Q^\star(a_{t+1},s_{t+1})\)价值最大的那个动作\(a_{t+1}\),而是选择价值最小或者是随机的动作,那么max带来的高估问题就能够被很好的解决了。但是选择价值最小,或者是随机动作没有意义,因为这很可能让估计的\(y_t\)和真实值偏差非常大,这样训练出来的Q网络没有意义了。
我们需要选择价值比较高的动作,但是这个动作不应该是让估计出来的\(Q^\star(a_{t+1},s_{t+1})\)价值最高的那个动作。
Double DQN就是这个思路,它估计TD target的值还是使用target network,但是具体选择动作是使用Q网络。这样选择value最大的动作,以及估计TD target就分为了两个部分:

DQN选择出来的动作,很大概率不是能够让target network估计价值最大的那个动作。这样就缓解了max操作带来的高估问题,因为根本就没有严格执行max操作:

Dueling Network
Optimal state value是指当前状态\(s\)下,理论上能够最大的期望动作价值。Optimal action value是当前状态\(s\)下,采用动作\(a\),理论上能够最大的动作价值。Optimal state value能够评价不同state的好坏,而Optimal action value能够评价当前状态下不同动作的好坏。Optimal action value减去Optimal state value就是采取某个动作后,相比较于期望动作价值的“优势”(实际计算出来的所谓优势是\(\leq 0\)的,因为Optimal state value等于Optimal action value的最大值)。
将Optimal state value看做是baseline,则优势函数advantage function的定义是动作\(a\)相对与baseline的优势,动作\(a\)越好,它的优势越大。

有了价值函数后,我们又可以用state value加上advantage来估计optimal action value,这能够帮助我们从新的角度估计optimal action value,进而优化DQN。
接下来,我们讨论价值函数的几个属性。首先存在定理: \[ V^\star(s_t) = max_a Q^\star (s_t,a_t) \] 为了证明这一点,可以推导: \[ V^\star(s_t) = max_\pi V_\pi(s_t) \\ = max_\pi E_{a_t\in A}(Q_\pi(s_t,a_t)) \\ = max_\pi \sum_{a\in A} \pi(a_t|s_t) Q_\pi(s_t,a_t) \] 继续推理, \[ max_\pi \sum_{a\in A} \pi(a_t|s_t) Q_\pi(s_t,a_t) = max_\pi 1 \cdot max_a(Q_\pi(s_t,a_t))=max_a Q^\star(s_t,a_t) \] 直观的理解就是,Optimal state value就是找到理论上最大价值的那个动作,让它的出现概率是\(1\)。
从这个定理出发,可以推导出,不同动作的最大动作优势\(max(A^\star)\)只可能是\(0\):
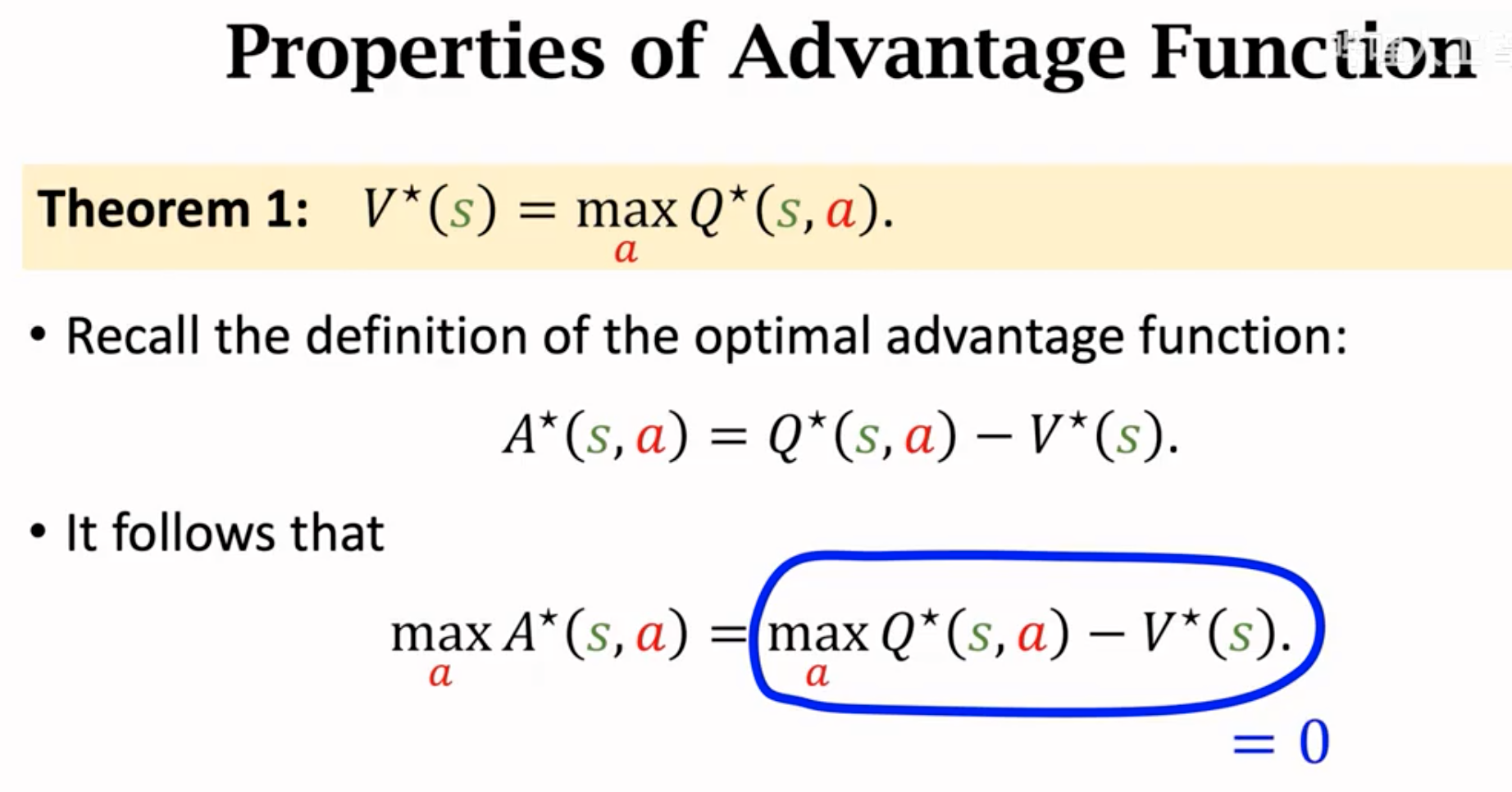
借助这个属性,我们构造了新的optimal action value的估计:

加了一个值为0的项。这个项似乎是多余的,但是它的意义是让学习\(V^\star\)和\(A^\star\)是唯一的。由于\(Q^\star\)是两个值的和,这两个值一个增大,另一个值减小,最后相加的和可以是不变的。也就是同一个值有不同的分解情况。由于\(V^\star\)和\(A^\star\)都是用神经网络估计的,这种不稳定性增大了训练难度,两个网络输出的改变反而可能有相同的总输出,增加了训练波动。


如果加上了理论值为0的\(-max(A^\star)\),就不是这样了。如果神经网络估计的\(A^\star\)减小或增大了,\(-max(A^\star)\)也会随之发生改变。这样训练如果发生波动,最后估计的\(Q^\star\)也会发生改变。
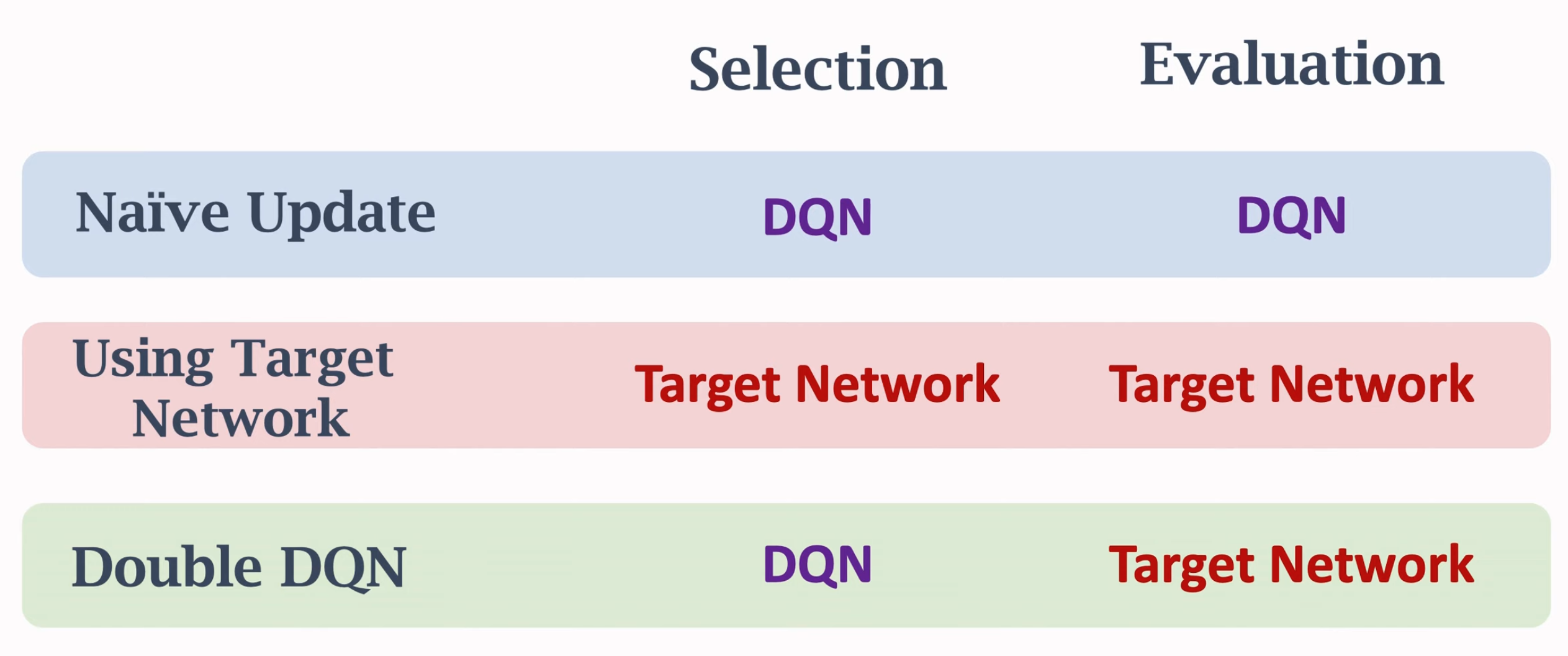
Dueling network就是利用定理二,来估计最优动作价值函数。设计两个网络,一个估计最优状态价值(输出一个实数),一个估计动作优势(输出关于动作的向量)。两个网络的输出结合,得到最终的最优动作价值。

Dueling network的结构,其输出与DQN完全一致,只不过有两个网络共同估计,一个网络输出的是\(V(s_t)\),一个网络输出的是优势\(A(s_t,a_t)\):
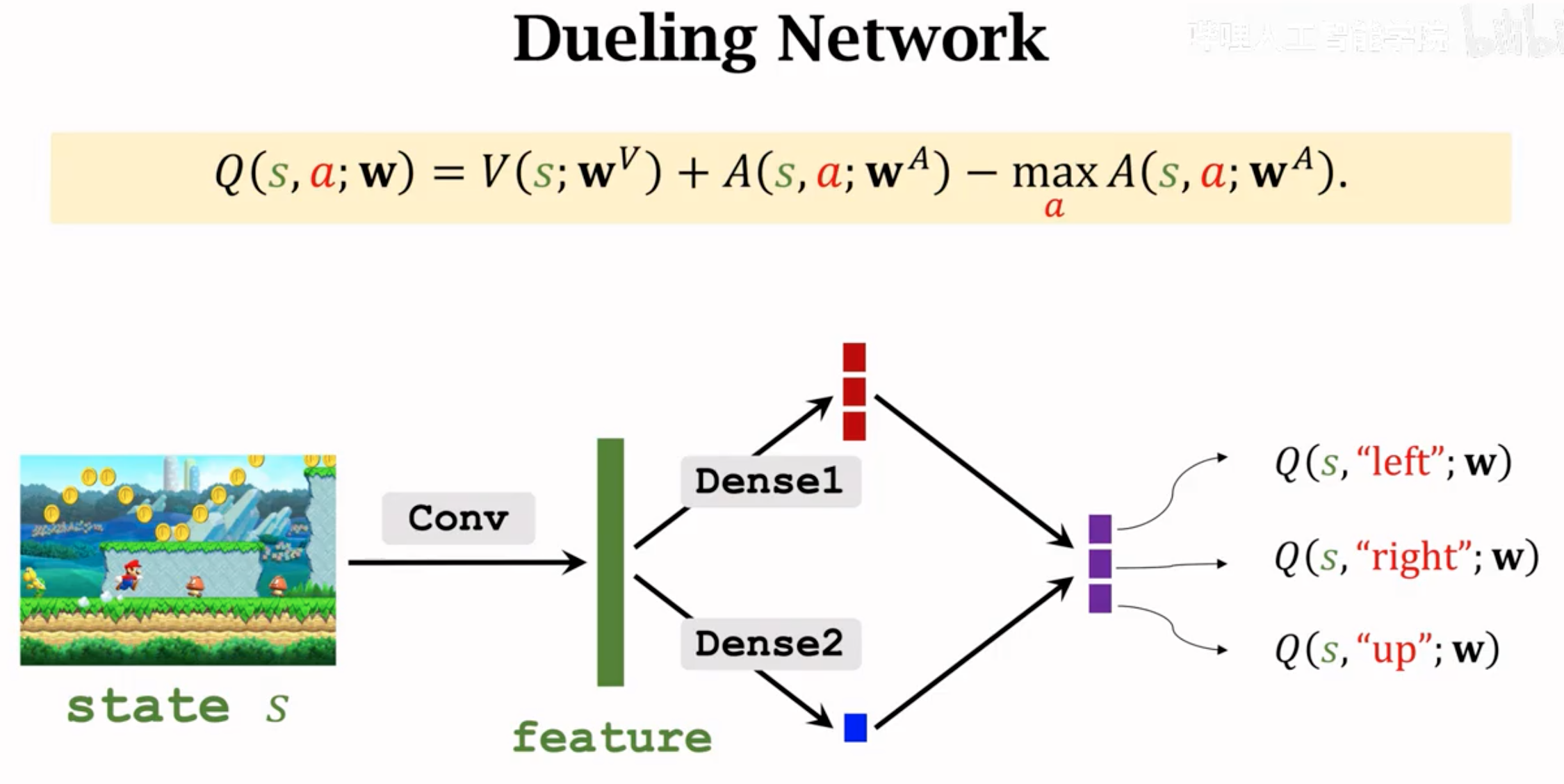
Dueling network的优化与DQN完全一致,使用Q-Learning算法估计TD target,计算TD error,然后梯度下降。
在实际中,大家发现如果把最后一项的max换成mean操作,效果更好:

Dueling估计出来的action value然后再根据一般的Q-learning进行更新。计算TD target(可考虑使用double DQN),然后更新。
Distributional Q-function
有研究者认为,前面的DQN估计的最优动作价值是一个期望,但实际上,可能真实的动作价值应该是一个分布。也就是说,不同的最优动作价值出现的概率不一样。如果只是单纯的让DQN估计最优价值期望的话,可能会丢失一些关键信息,比如说不同的动作价值分布完全可以有相同的期望:

学习这种最优动作期望的分布,能够帮助我们更好的进行估计。将动作期望限制在一定范围内,然后划分不同的bin:
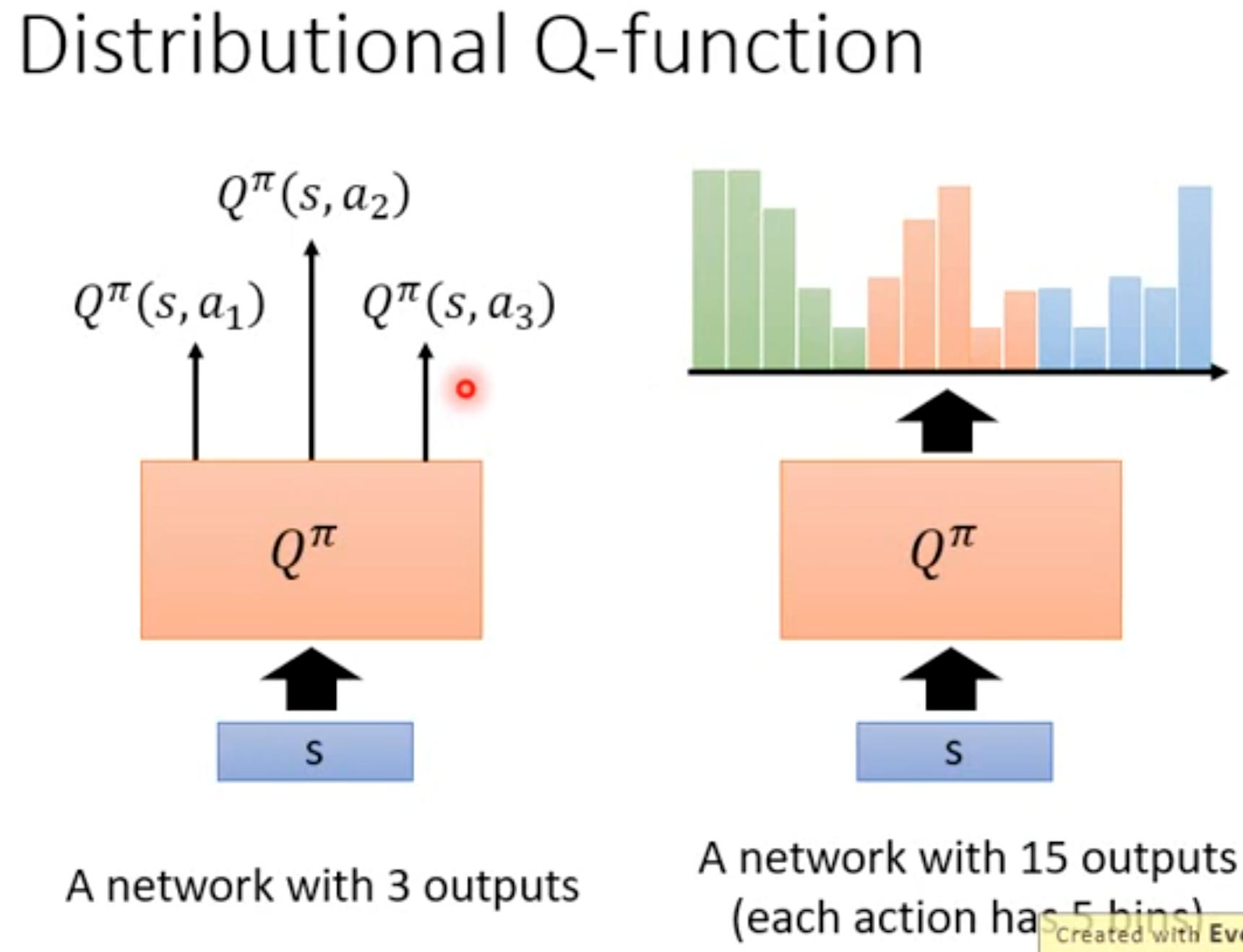
不过最后DQN选择哪个动作的时候,一般还是依据各个动作价值分布的平均。不过这种分布本身能够帮助我们不仅仅是依赖于平均值进行动作的选择,比如我们可以依据价值分布的方差来进行选择,方差大的动作代表它的风险比较大,随后有概率获得比较好的奖励,但也有可能奖励非常低,这样能够帮助agent学会规避风险。
3. 策略学习Policy Learning
我们想要学习另一种RL agent可以做决策的方法,训练policy。policy是一个关于状态的概率函数\(\pi(a_t|s_t)\),输入状态,输出动作概率。依据policy动作概率采样之后,得到\(t\)时刻的动作\(a_t\)。
这个policy的实现可以是一个概率表格lookup table,输入什么状态,然后根据概率采样就行。但是很多任务下,输入的状态是非常复杂的,不可能穷举所有的输入状态。因此需要用参数化的方法,根据各种输入,经过参数计算之后,给出固定范围的输出。参数化可以是一个线性分类层、核函数或者是一个神经网络,用\(\mathbf{\theta}\)表示policy的参数:
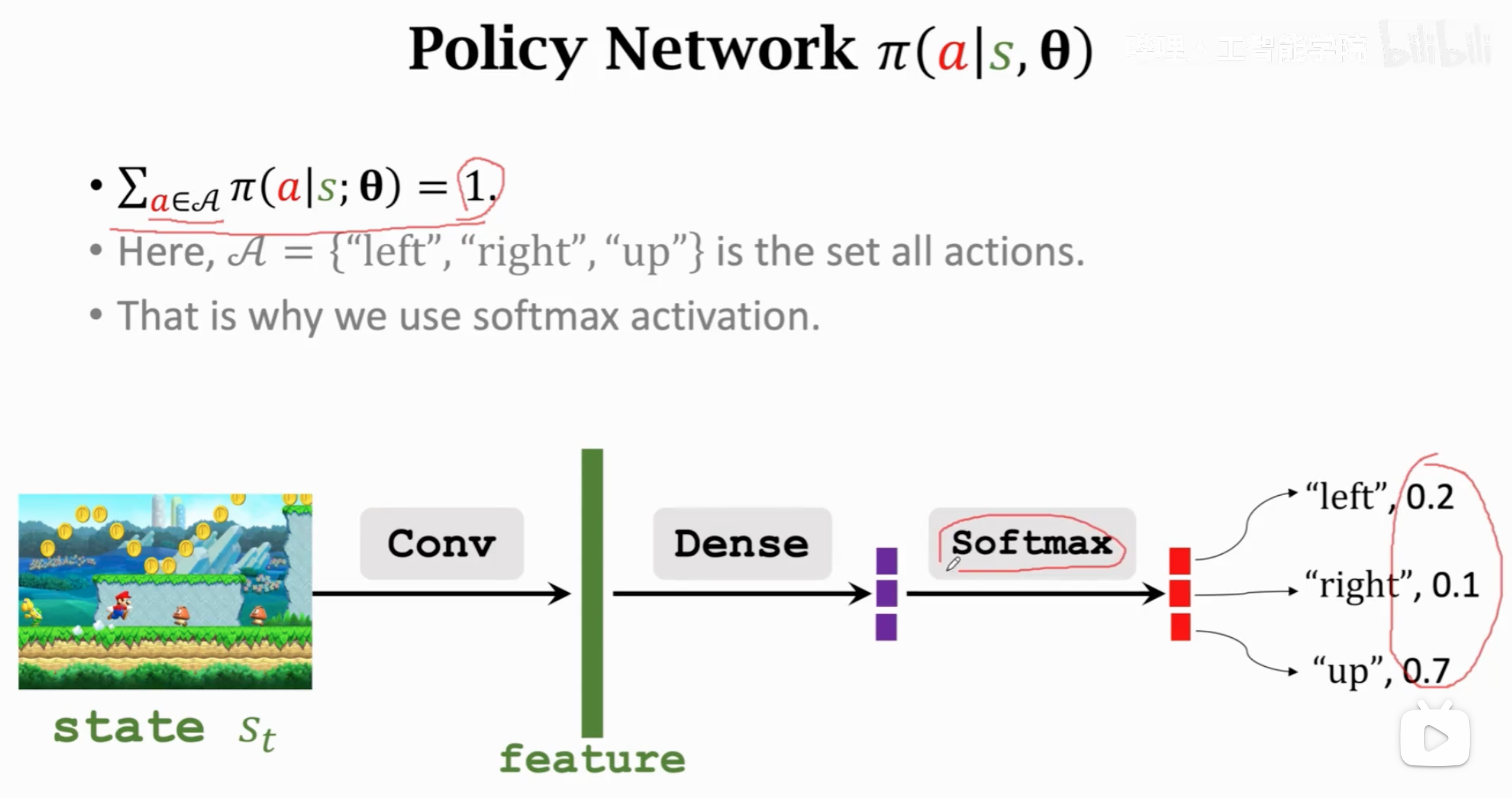
在定义了policy的实现之后,我们就要优化它。怎么评价一个policy的好坏呢?一个好的policy,在当前状态下,如果它总是能够让未来的奖励期望更大,那我们可以说它是更好的。也就是说,用当前状态的state value function来衡量policy好坏。
Policy Gradient Ascent
目标就是让state value function最大,优化算法就是policy gradient ascent:

接下来来讨论如何计算policy梯度。

假设动作是离散的,则策略梯度的第一种形式如下所示。下面的推导假设动作期望\(Q_\pi\)是一个常量,但实际上不准确。不过推导的结果是一样的。

在拥有这个公式之后,对于离散动作,我们就可以求policy gradient,然后优化policy:

如果动作是连续的,那我们就需要求积分,继续进行推导:

上面的推导(不严格)把策略梯度求积分,转化为了对动作的期望。state value本来就是一个期望,state value对\(\theta\)求导也被转化为了一个期望。这个期望值还是与动作有关。
对于连续动作,尽管我们计算出里面项的值,但是求积分是很困难的。所以这个期望只能估计,估计的方法使用蒙特卡洛估计。蒙特卡洛估计就是用不断的随机抽样的平均值,去逼近真实的期望值。该方法的核心定理就是大数定理。
具体做法如下所示。


抽样一个随机动作,计算期望里面项的值\(\mathbf{g}\),这个值作为策略梯度的一个无偏估计,用来更新policy参数。具体的算法流程如下所示:
 接下来对policy gradient的计算过程进行优化。policy gradient的计算是用希望最大化state value,而state value是当前局势state的价值期望。用state value对policy的参数\(\mathbf{\theta}\)求导:
接下来对policy gradient的计算过程进行优化。policy gradient的计算是用希望最大化state value,而state value是当前局势state的价值期望。用state value对policy的参数\(\mathbf{\theta}\)求导:

上面的公式里得到的梯度是一个期望,但是很显然我们是计算不出来期望的。所以要用蒙特卡洛估计进行随机梯度上升。这个随机抽样的动作\(a_t\)计算得到的梯度有很强的随机性,也就是说方差很大,这会让强化学习收敛变慢,优化过程非常不稳定(震荡)。为了解决这一问题,可以引入baseline(注意和一般监督学习里的对比方法baseline做区分)。这里的baseline是指独立于动作\(A_t\)的任意函数,它是一个无偏估计,加入以后不会改变策略梯度的真实期望。baseline与\(\partial~ln~\pi()/\partial~\mathbf{\theta}\)相乘后的期望能够保证是\(0\):
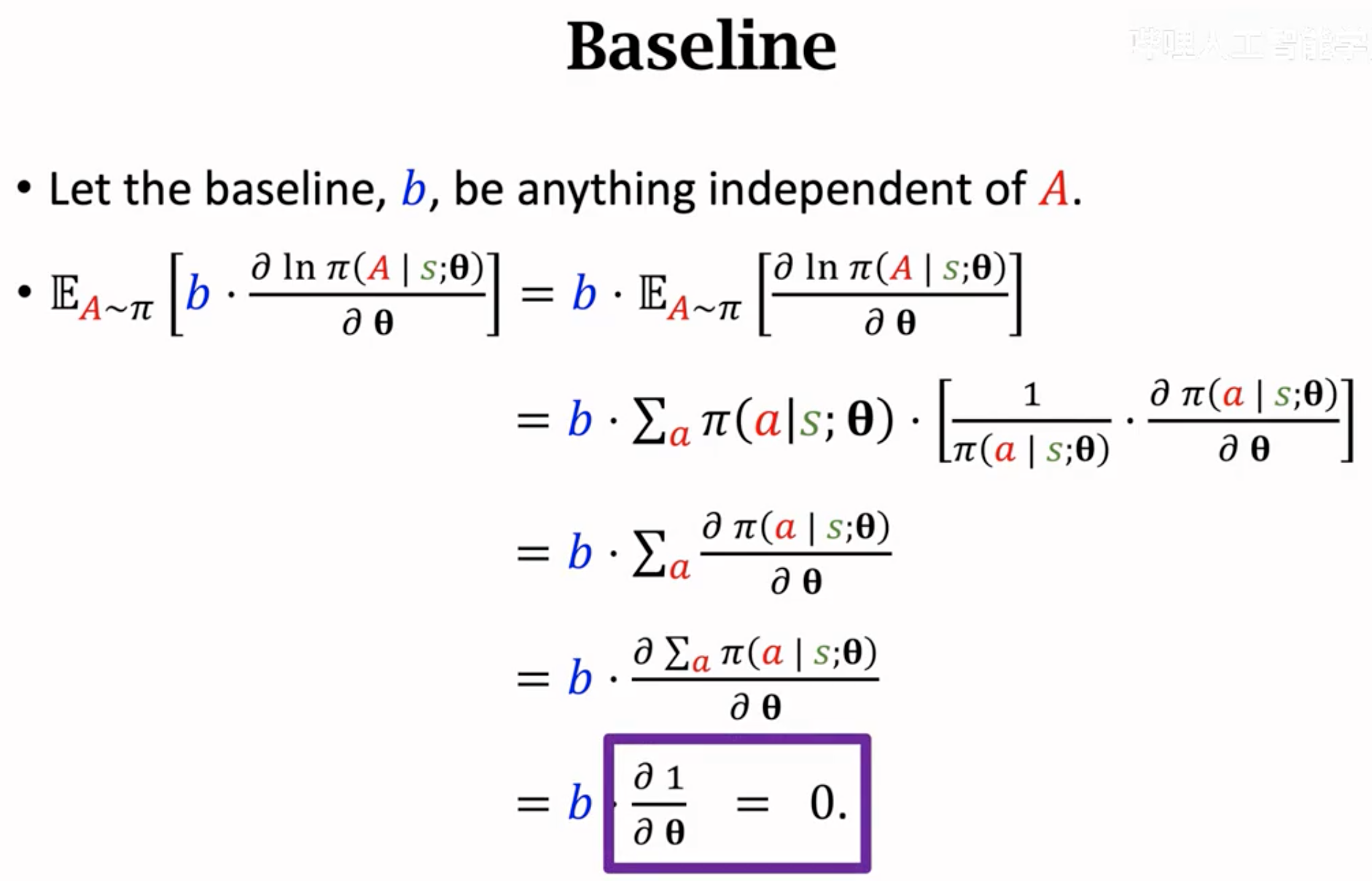
也就是说,如果让baseline加入到policy gradient的计算过程中,仍然可以保证和原来的值相同:
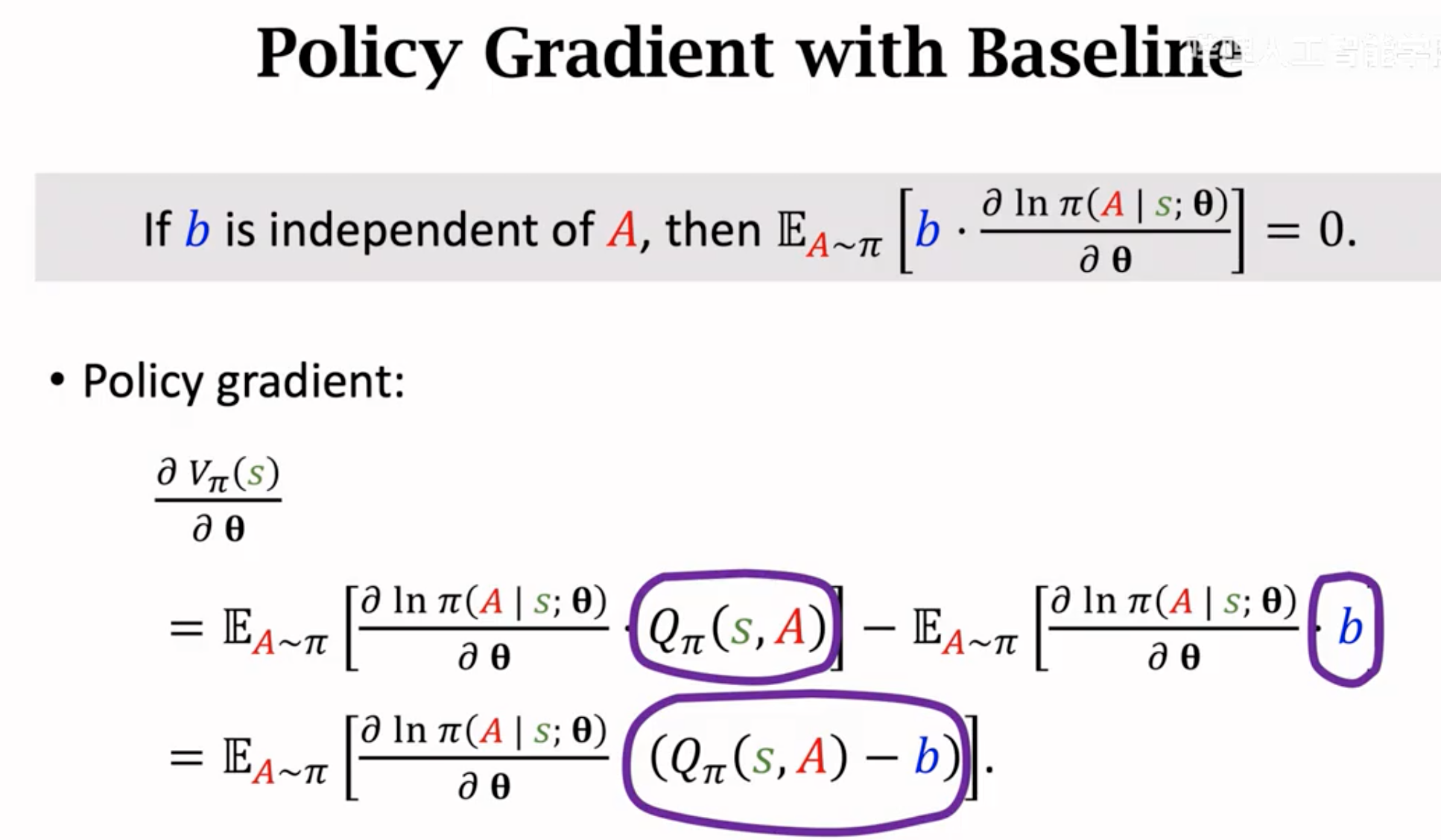
baseline不改变理想的policy gradient,但是它对于蒙特卡洛抽样估计出来的梯度有帮助。假设有很多个随机抽样出来的动作\(a_t\),每个动作都计算带有了baseline的policy gradient。如果baseline和动作价值\(Q^\pi(s_t,A_t)\)比较接近的话,带有baseline的policy gradient的方差会更小。


那么baseline怎么选择呢?它首先一定不能依赖于具体动作的选择,一种常见的做法是直接用状态价值来作为baseline。状态价值是当前形式下各个动作价值的平均,最后到底选择哪个动作对于状态价值没有影响。并且,状态价值不是一个完全随机的函数,它的值应该是和动作价值\(Q_\pi\)保持在一定范围内的:

下面是李宏毅的深度强化学习课程里对policy gradient的解释,本质上与上面的推导过程是一样的,不过能够更好入手。我们训练的policy就是想要让它做的动作能够得到的奖励更大。这个奖励不应该是只考虑当前时刻的奖励,而是未来的累积奖励。如果只考虑当前的话,一个问题是很多动作没有奖励,另一个问题是会让policy目光短浅,不考虑能不能达到最终的目的。并且我们希望的是在各种情况下,综合起来能够得到奖励期望最大。对于一个收集的轨迹,它出现的概率为:
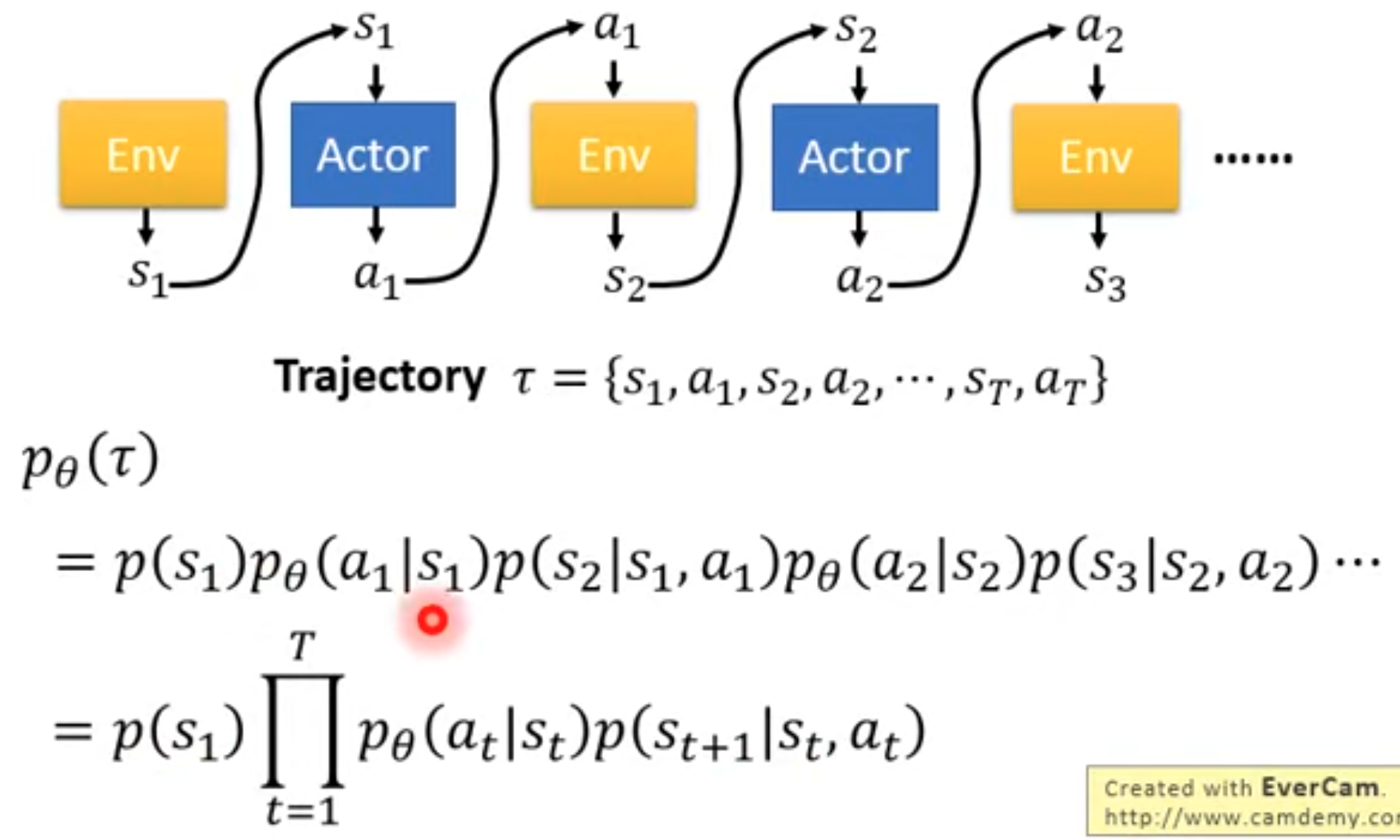
每个收集的轨迹能够累积的奖励,乘以它出现的概率,就是累积奖励期望:
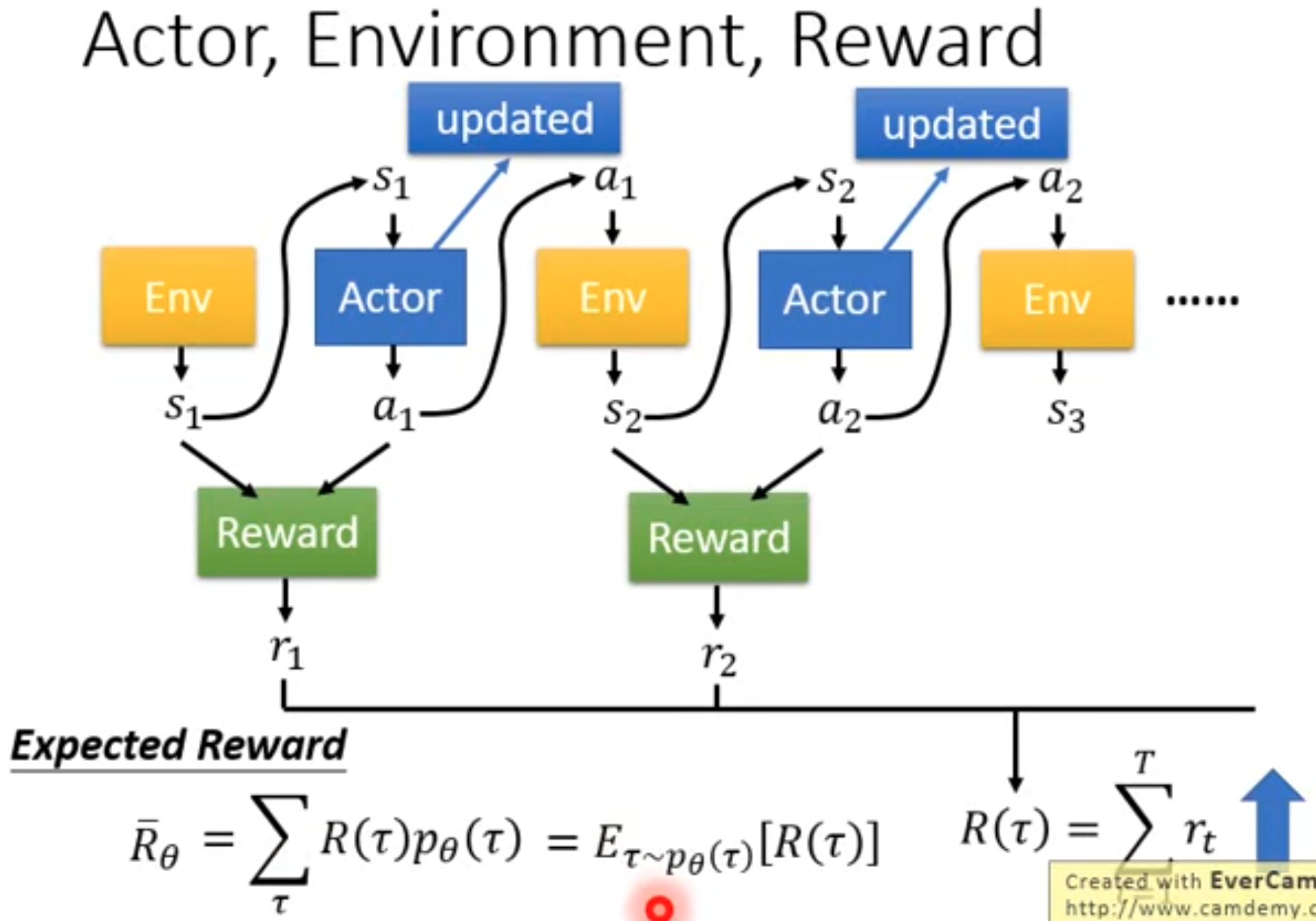
很显然,轨迹的出现是依赖于policy的,它与policy有关。这个各种不同轨迹的奖励的期望,事实上就是一开头推导的state value。对累积奖励的期望求梯度,就得到了policy gradient:
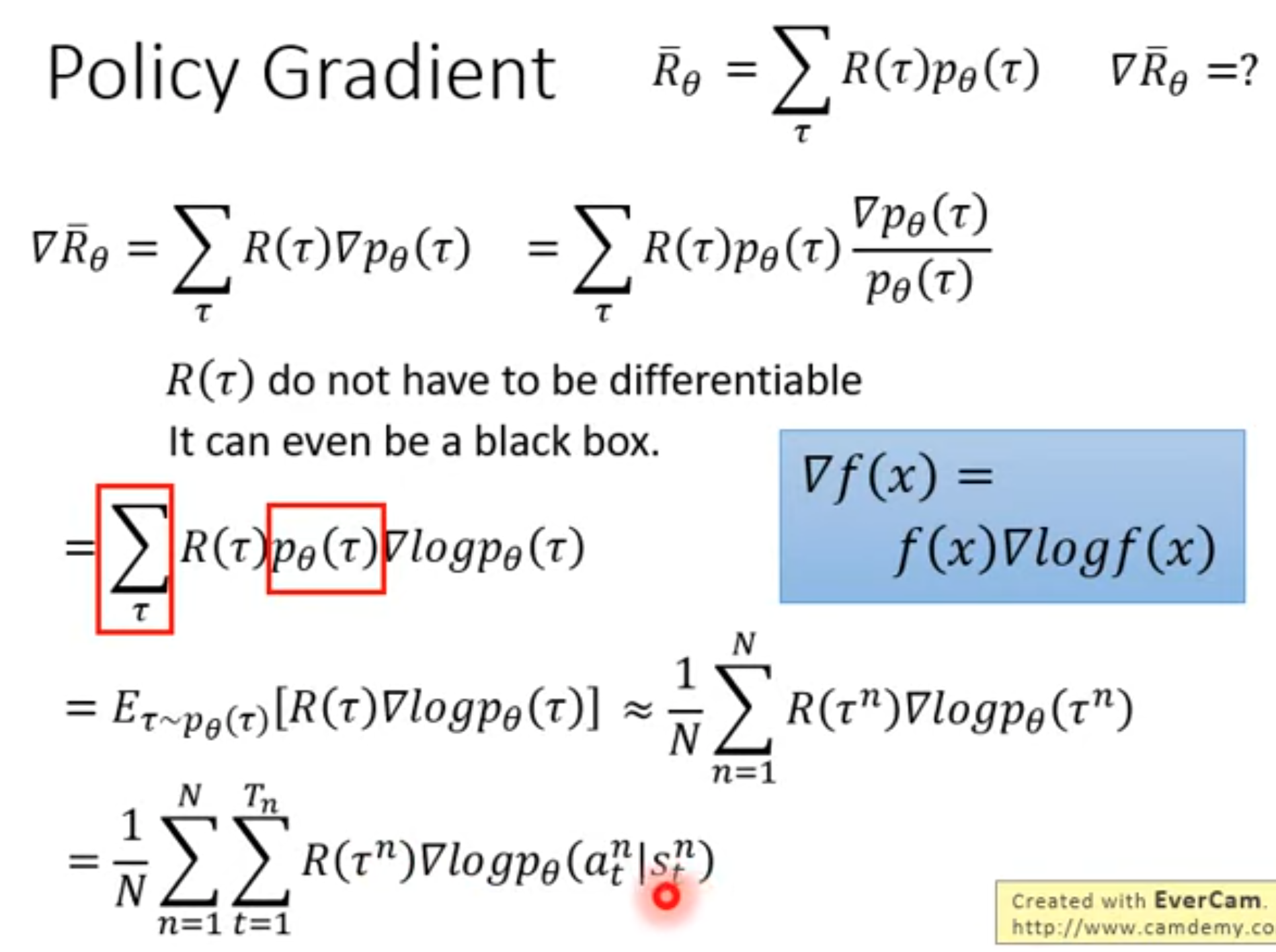
对于上面的式子,虽然看起来里面有一项是轨迹的累积奖励,而不是我们在开头推导出来的action value \(Q\)。但是这个式子是不完善的,因为让轨迹上的每个action都有相同的累积奖励是不合理的,有的动作应该累积奖励大,有的动作造成的累积奖励小。所以,我们还是会使用从这个动作之后产生的所有奖励,并且乘以discount factor做衰减。这样的话就是我们上面得到的最终policy gradient了(下面的公式里带上了baseline):

我们可以进一步理解这个policy gradient,它的左边是policy输出概率的log似然对参数的求导。我们看成有个虚拟的、让选择的动作\(a_t\)对应的真实被选择概率是\(1\)。我们让这个似然最大化进行优化,就是最小化它的交叉熵,也就是让动作\(a_t\)对应的被选中的概率进一步增大。而右边的项是一个动作对应的累积奖励(动作价值action value),它就是评估选择这个动作到底好不好,能带来多大的奖励。如果这个动作足够好,带来的累积奖励大,那么就作为梯度权重,让policy朝着动作\(a_t\)被选中的概率增大的方向进行优化。反之,就让它被选中的概率减小。
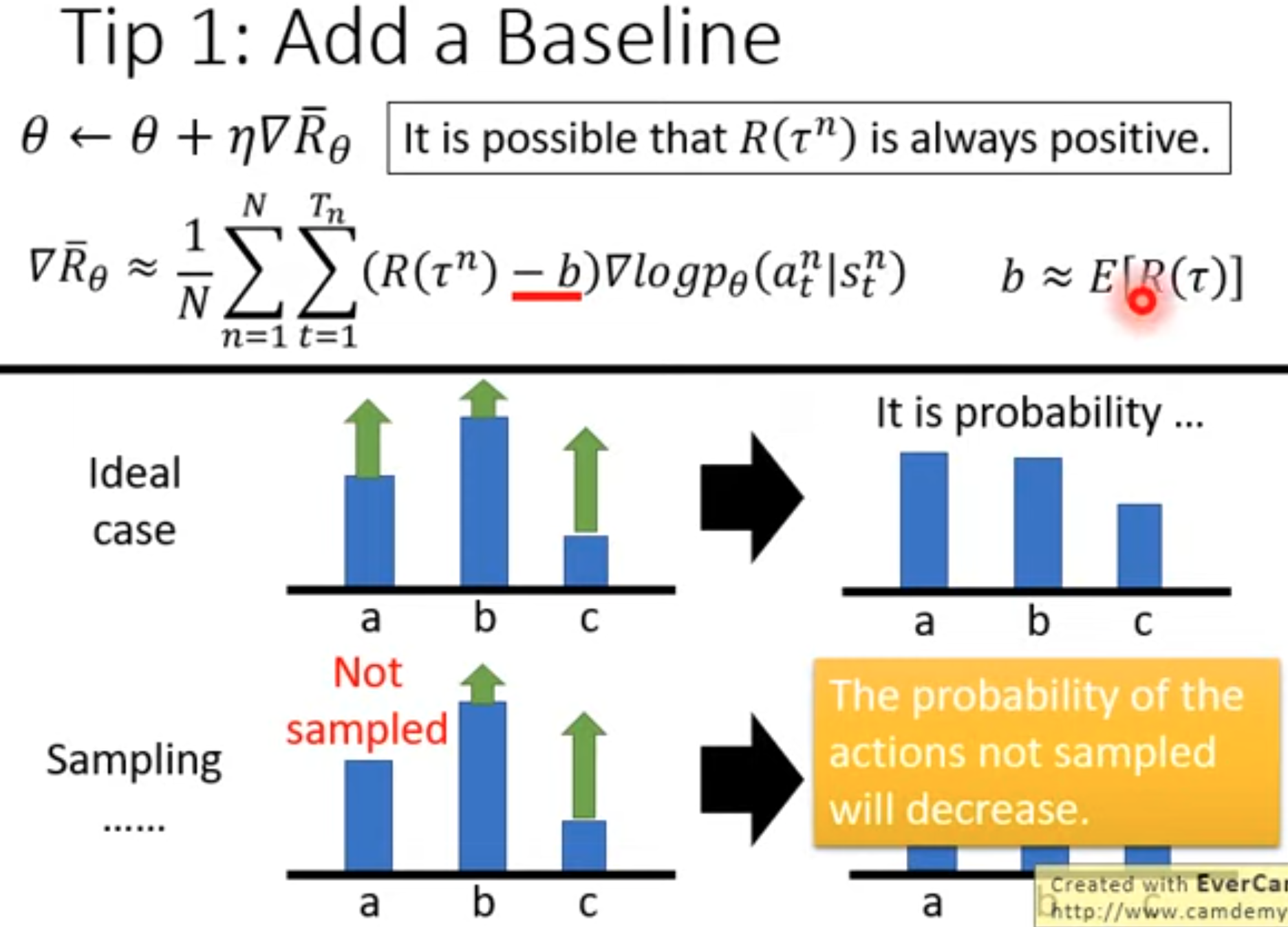
而用动作价值减去baseline的一个意义是,不要让所有的梯度权重都是正的。因为很多reward设计的时候,可能都是大于0的。这就是会潜在的让每个被选中的动作下一次被选中的概率继续增大。如果每个动作被选中概率被增大的程度一样就好了,但是是不可能的。因此,选择一个和具体选哪个动作无关的函数作为baseline,这个baseline能够帮助我们评估每个动作带来的相对累积奖励,也就是所谓的优势(advantage)。baseline消除了每个动作的“固有价值”,而只关心相对价值。下面的图是李宏毅老师提供的一个解释:
REINFORCE
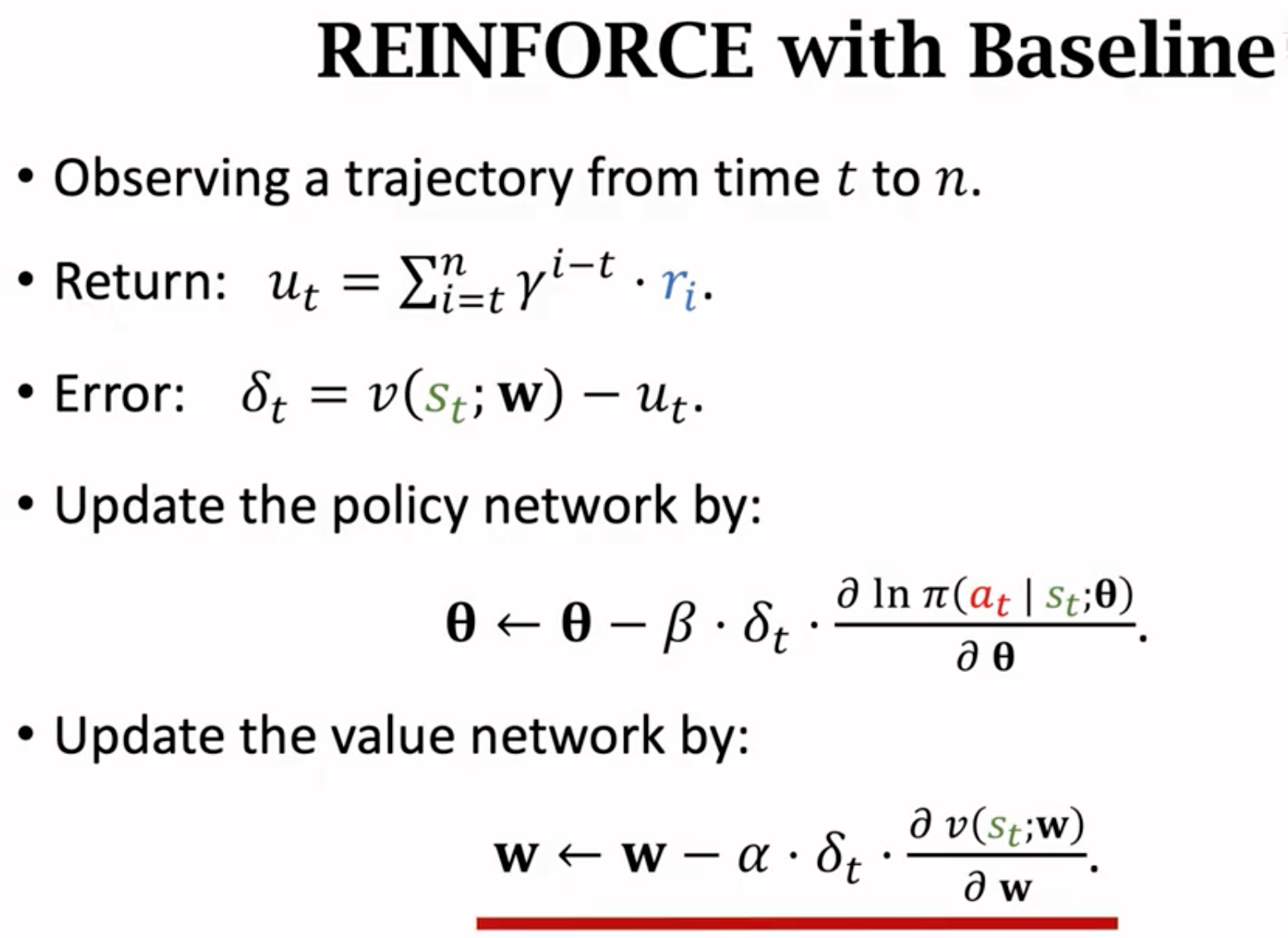
上面流程的一个未解决的问题(第3步),就是到底如何知道动作价值\(Q_\pi\)?这个值也是期望值,我们没有ground-truth的期望值,只能估计。第一个方法是REINFORCE,利用agent完整的进行一轮交互,然后计算观测到的累积奖励\(u_t\),用这个观测到的累积奖励\(u_t\)来作为期望\(Q_\pi=E(U_t|s_t,a_t)\)的估计值:
 上面的计算能够估计得到\(Q_\pi(s_t,a_t)\)。接下来如果考虑加入baseline,还需要估计\(V_\pi(s_t)\)。如何估计?再引入一个value network来估计state value:
上面的计算能够估计得到\(Q_\pi(s_t,a_t)\)。接下来如果考虑加入baseline,还需要估计\(V_\pi(s_t)\)。如何估计?再引入一个value network来估计state value:

这样为了得到policy gradient,我们做了两次蒙特卡洛估计和一次用神经网络的估计:

一个典型的带有baseline的REINFORCE方法的设计:
更新policy network,只需要计算带有baseline的gradient就好(借助value network估计的state value作为baseline)。而更新估计state value的value network,我们希望value network的输出,就尽量和观察到的累积动作价值\(u_t\)相近(虽然\(u_t\)是对动作价值\(Q_\pi(s_t,a_t)\)的观察,而不是状态价值\(V_\pi(s_t)\)的观察,更加精准的状态价值的估计应该是采样不同动作让任务完成,得到对应不同动作的多个\(u_t\),然后再与动作概率相乘得到状态的观察。但是显然这种做法代价太过于承重,难以实际应用。而且考虑到单个\(u_t\)虽然不够精准,但它同样是会被用来估计状态价值的,所以我们也可以强迫state value network去向\(u_t\)靠拢)。


带有baseline的REINFORCE方法总结:

第二个方法就是我们再使用一个网络来估计动作期望,这个网络就是critic网络。该算法是Actor-Critic方法,这个方法不需要完整的跑完一个流程到任务终止。下面一节进行详细描述。

Trust Region Policy Optimization
trust region优化是数值优化中的一类算法。下面介绍推导过程。一般的随机梯度上升算法通过随机采样来避免优化目标函数\(J\)是期望时,对期望\(J\)进行直接求导(由于期望是定积分函数,它的求导可能很困难):

随机梯度优化方法具有很大的随机性。置信区域优化算法中置信区域trust region的定义:
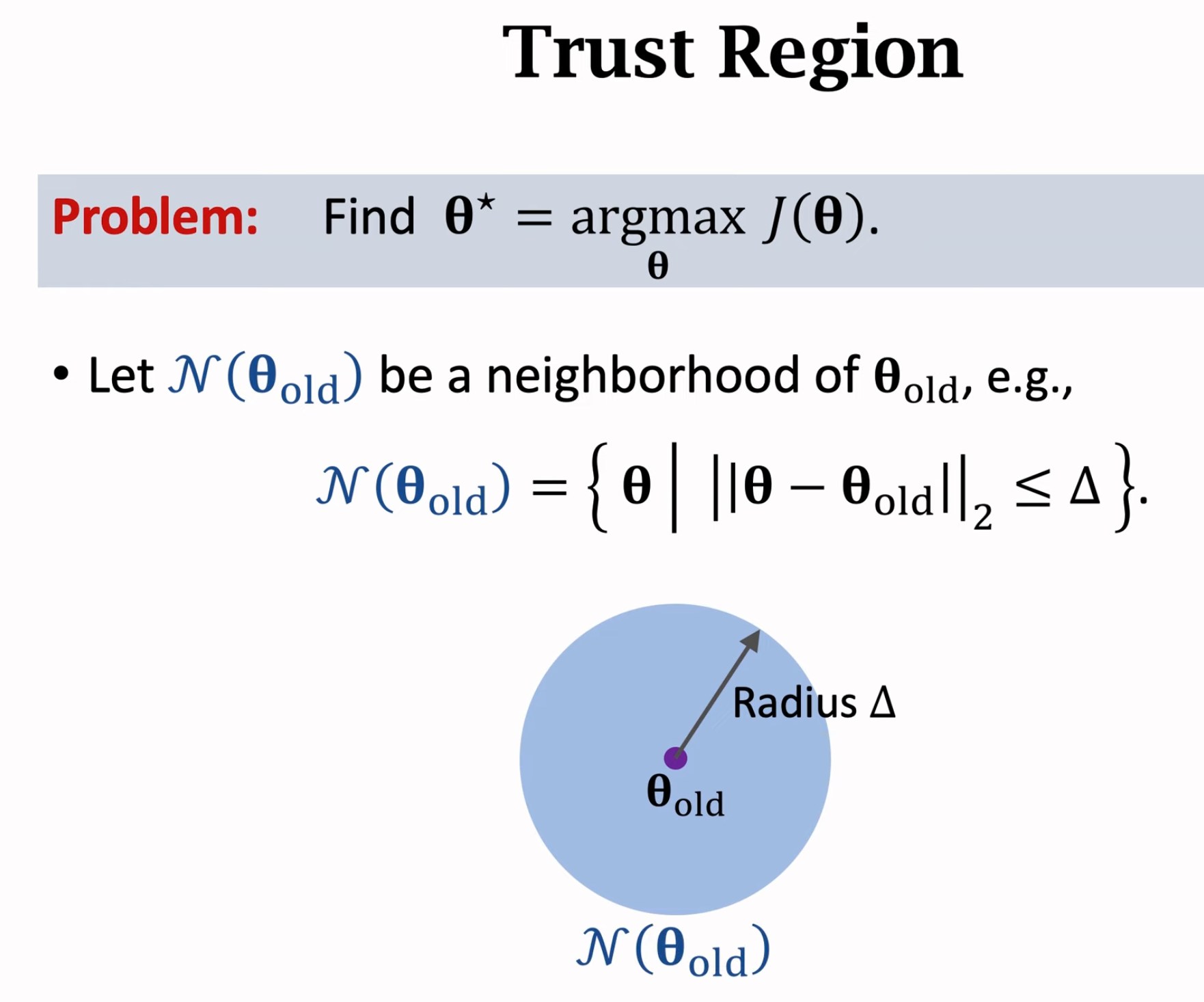
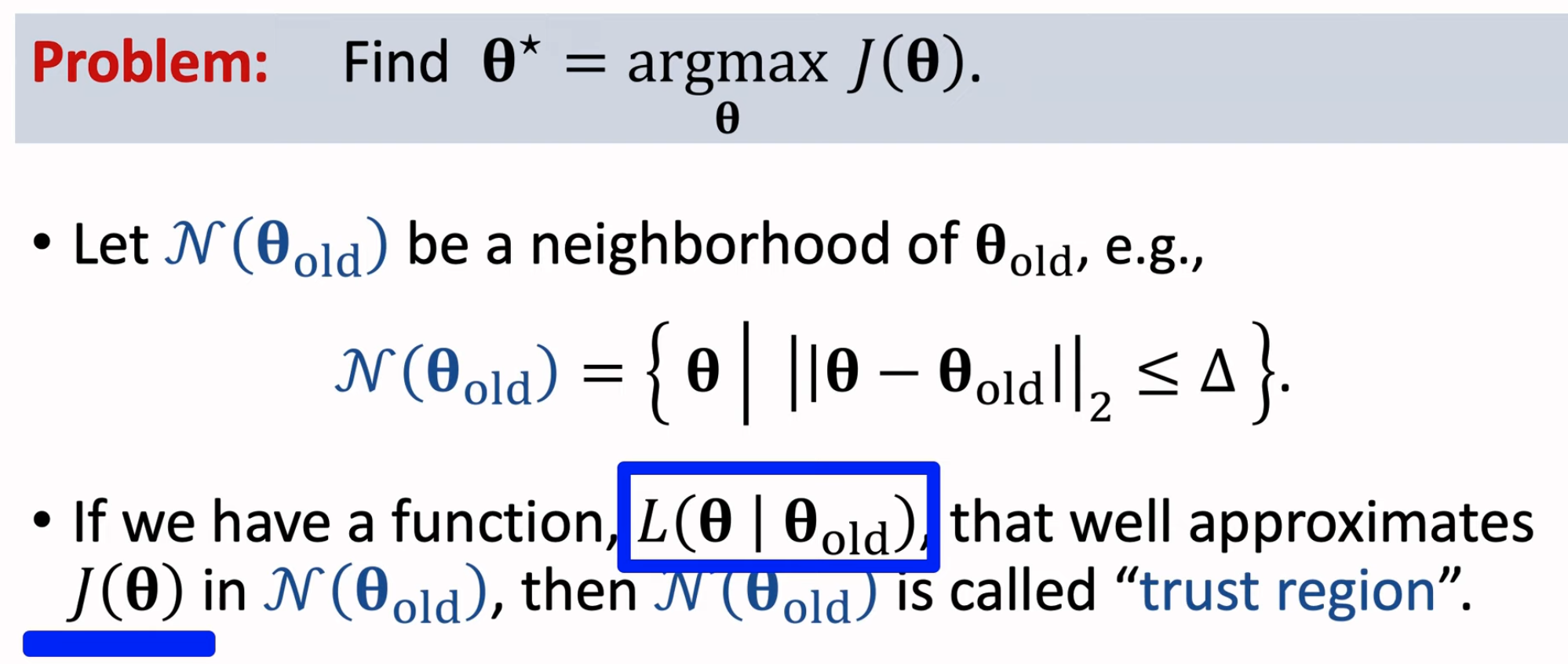
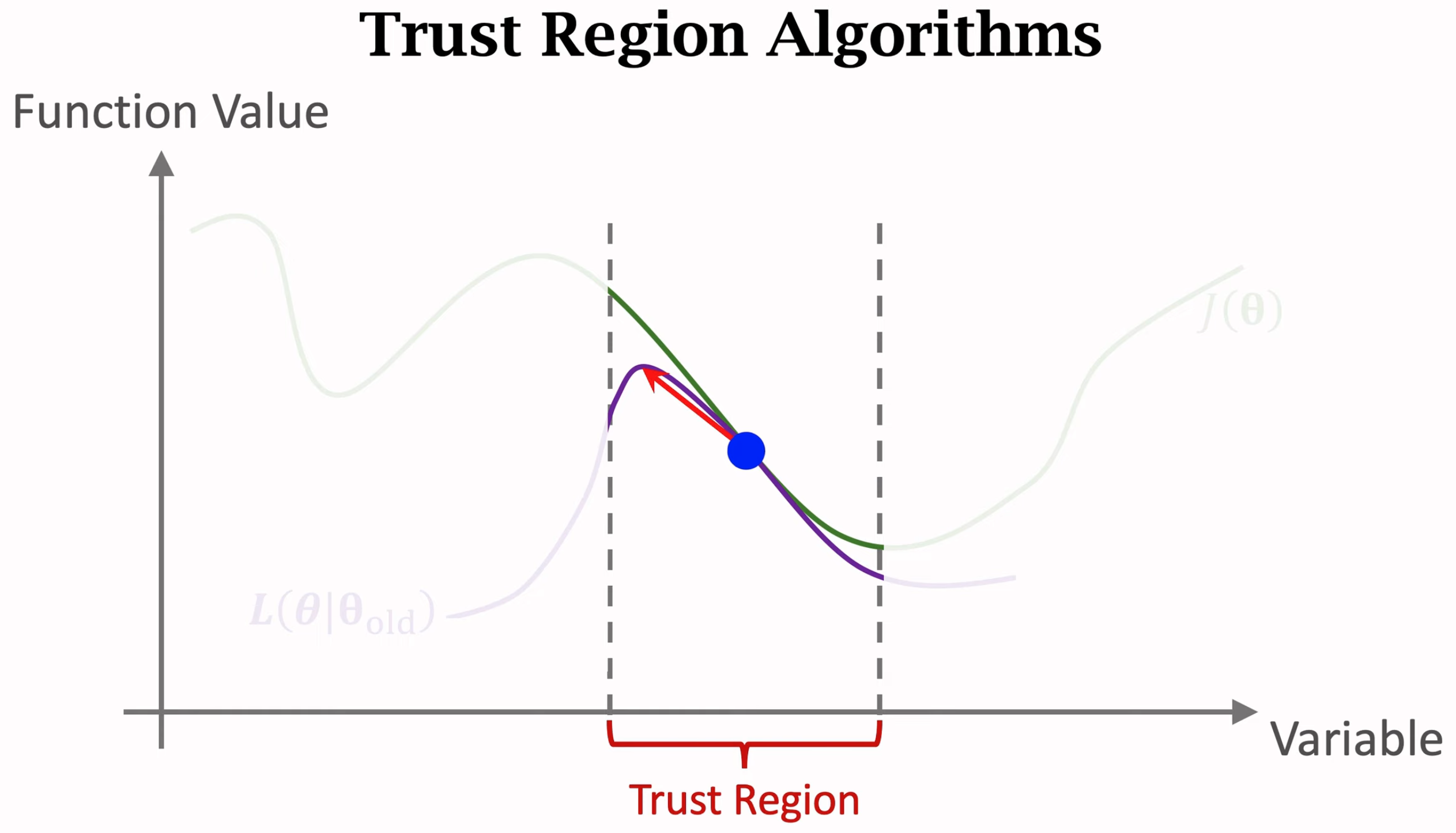
trust region就是在当前参数\(\theta\)周围的一个领域,在这个领域上可以找到一个能够和目标函数\(J\)相近的更为简单的新函数\(L\)。我们不直接优化目标函数\(J\),而是通过优化更为简单的新函数\(L\)来找到新的参数\(\theta_{new}\),\(\theta_{new}\)能够让新函数\(L\)的值更大,也能够让目标函数\(J\)更大。
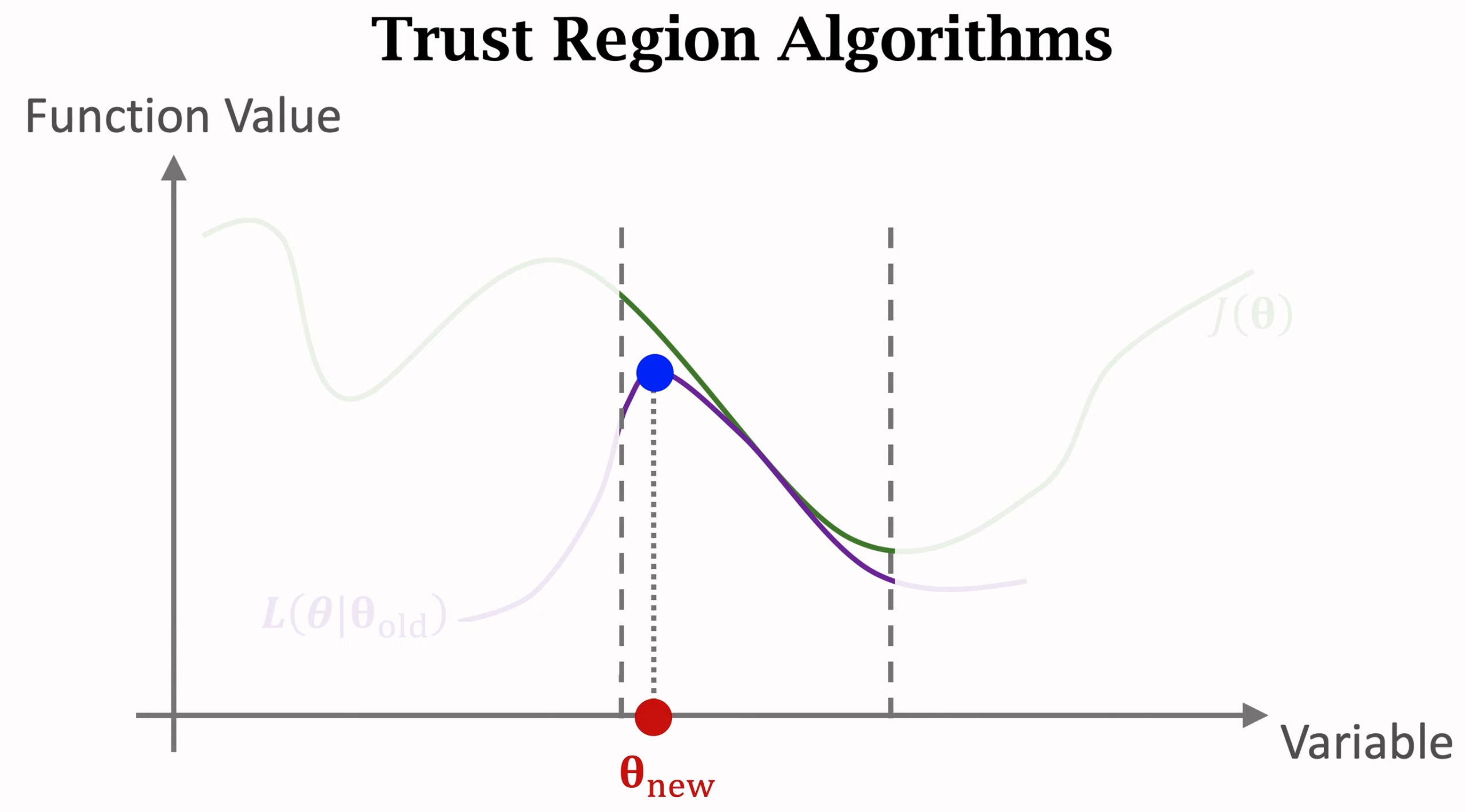
trust region优化算法有两步,第一步是找到领域,然后构造新函数\(L\),这个函数在领域上的值能够非常靠近目标函数\(J\)。要构造新函数\(L\),有很多手段,就直接的就是用蒙特卡洛估计方法得到一个关于目标函数\(J\)的估计。第二步是利用新函数\(L\)更新参数,找到能够让函数\(L\)更大的新参数。第二步就可以利用一般的梯度上升算法,第二步一定要保证新的参数还位于trust region范围\(\Delta\)内,不能超出该范围。如果超出该范围,在新函数\(L\)不改变的情况下,不能保证新函数\(L\)和目标函数\(J\)之间的差异还保持在一定范围内。

将trust region优化算法应用到policy优化问题上,就是TRPO算法。policy优化的目标是能够使state value期望最大,引入一个旧参数用于采样,这样把on-policy改为了off-policy的方法:


应用trust region优化算法,第一步估计新函数\(L\),使用蒙特卡洛估计:

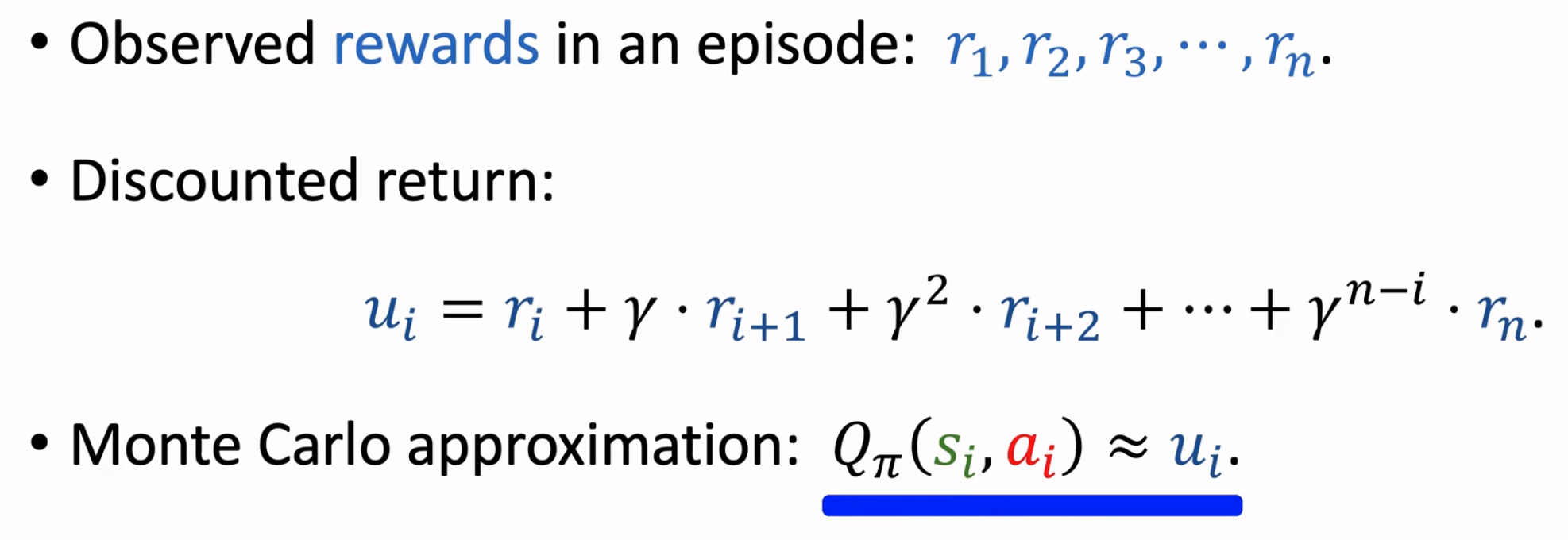
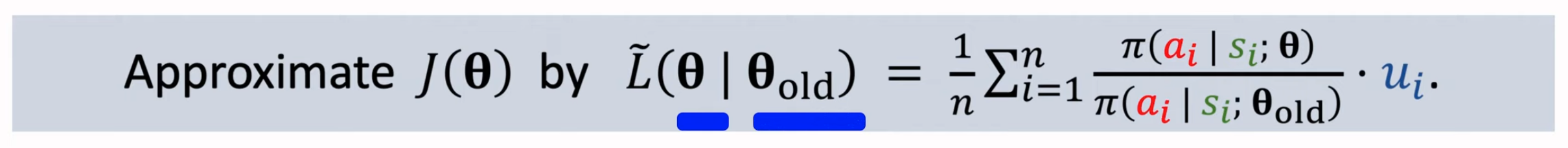
第二步进行带有约束的最大化:

TRPO算法相比于上面的REINFORCE方法的好处在于,不需要每次更新policy参数,都需要重新与环境交互得到新数据。而是可以一次数据采样,多次更新。不需要采样数据的网络和待更新的policy是同一个网络。但是它的缺点在于,第二步优化是一个带有约束条件的优化,它的优化不够简单,下面小节介绍的PPO算法优化更加简单。
Proximal Policy Optimization
在前面提到的REINFORCE方法中,包括其他的on-policy方法需要policy不断的与环境交互去生成数据,用来计算policy gradient。这种方法的最大缺陷就是采样数据需要消耗大量的时间。每次policy参数更新之后,都需要重新与环境交互去生成新的训练数据。那么有没有一种方法能够一口气采样很多数据,也能够让policy不断的更新呢?这就是off-policy方法需要解决的问题。
解决这个问题的关键在于policy gradient的实际计算是通过符合policy当前参数的动作概率进行采样得到的,如果想要实现off-policy,就需要想办法在数据采样的分布与基于policy不断更新的参数的预测概率分布不同的情况下,计算得到正确的policy gradient。
解决方法是可以依赖importance sampling思想。这个方法是一种通用的思想:

通过一个简单的变换,我们可以将符合\(p\)分布的变量\(x\)对应的函数\(f(x)\)的期望,转换为在符合另外一种分布\(q\)情况下的函数\(f(x)p(x)/q(x)\)的期望。这个importance就是指\(p(x)/q(x)\),原概率分布相对于新概率分布的差异,作用类似于权重。如果\(p(x)\)越大,而\(q(x)\)越小,则作为权重增大;如果\(p(x)\)越小,而\(q(x)\)越大,则作为权重减小;如果\(p(x)\)与\(q(x)\)增大减小的趋势非常相近,则作为权重接近\(1\)。
上面这个操作在TRPO中已经介绍过,这里只不过是从权重的角度重新思考。
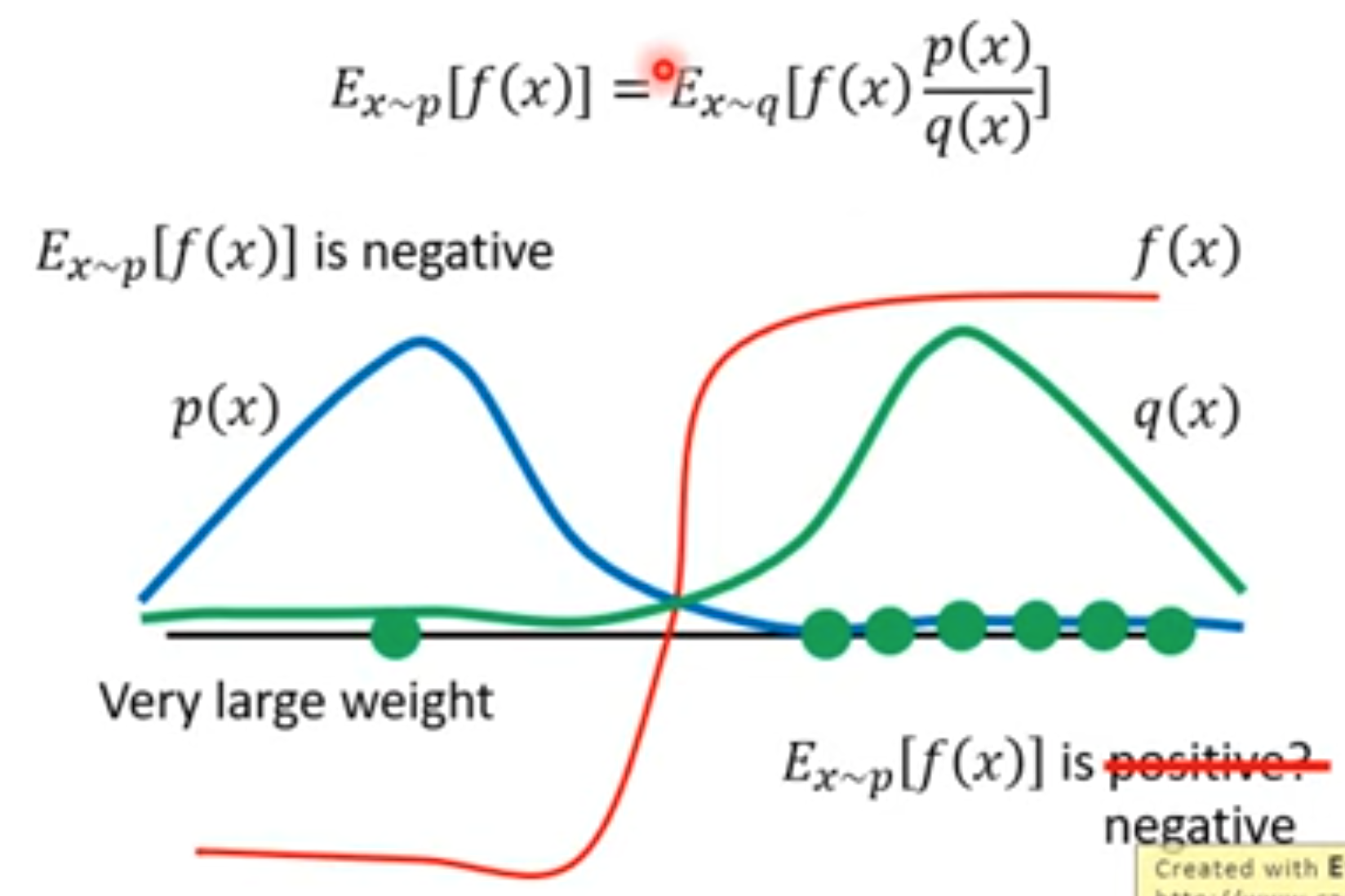
尽管变换前后期望保持不变,问题在于方差会发生改变,特别是在\(p(x)\)与\(q(x)\)差异很大的情况下。

由于变换前后的方差可能发生很大的改变,而我们是使用采样的方法进行估计的,方差差异大的情况下估计出来的期望也很可能不同。只有不断的大量采样,才有可能在使用两个差异大的\(p(x)\)与\(q(x)\)的情况下,估计出来的梯度相同。下面是一个例子说明。在利用原概率\(p(x)\)采样(蓝色线)的时候,估计出来的期望应该是一个负数。而在利用另一个概率\(q(x)\)采样(绿色线)次数不够多的时候,它主要集中在右边绿色的点。利用这些结果估计出来的函数\(f(x)\)的期望可能变成一个正数。而只有大量的采样,例如采样到了一个变量\(x\)是左边绿色的点,它的\(p(x)/q(x)\)是很大的值,把它加入到平均计算过程中,有可能能够让期望修正为负数。
把importance sampling思想运用到off-policy方法中。就是要修改最大化价值的梯度:

采用其它的参数\(\theta^\prime\)负责收集数据。继续推导,得到新的梯度计算公式与要优化的object function:

再回想下前面提到的不能让概率\(p(x)\)与\(q(x)\)差异太大,防止方差差异态度,估计不准确。PPO为了解决这个问题,增加了一个让参数\(\theta\)和参数\(\theta^\prime\)预测的行为差异不要太大的约束:


在PPO的算法里,使用上一轮的policy参数\(\theta^k\)与环境互动,产生一系列的交互数据和对应的advantage。然后,更新policy的参数\(\theta\)。在优化的过程中,会动态地调整KL约束的权重\(\beta\)。当KL散度很大的时候,要增加权重\(\beta\),让优化的新参数\(\theta\)的行为不要和采样数据\(\theta^k\)偏离太大;当KL散度很小的时候,这时候代表\(\theta\)和\(\theta^k\)的行为太相似了,这不是RL优化的目的,因此要减小权重\(\beta\),让参数\(\theta\)能够与数据\(\theta^k\)的行为有一定差异。
上面的PPO算法还有一个问题是计算KL散度的时候,理论上是应该有大量的state,输入参数\(\theta\)和参数\(\theta^k\),这样才能够比较他们两个的行为差异。所有存在一个PPO2算法,能够自动的调整优化目标函数:
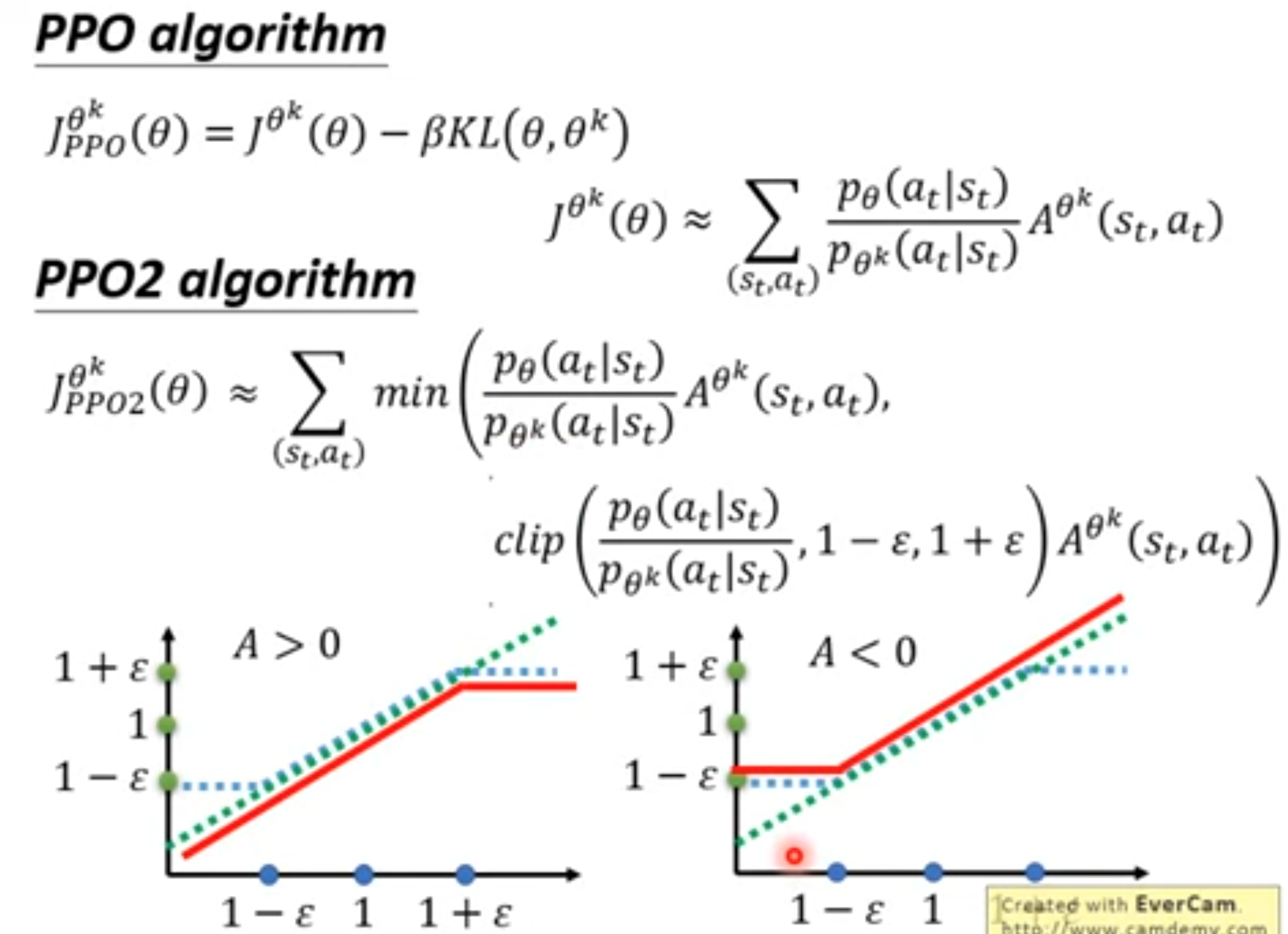
上面的红色是最后选择的objective function,横坐标是\(p_{\theta}/p_{\theta^k}\)。如果advantage大于0,希望增大动作\(a_t\)的出现概率\(p_\theta(a_t|s_t)\),但是当优化\(p_{\theta}(a_t|s_t)/p_{\theta^k}(a_t|s_t)\)超过\(1+\epsilon\)的时候,两个概率差异太大,不能继续优化,这时候objective function直接变为\((1+\epsilon)A^{\theta^k}\)。如果advantage小于0,需要减小动作\(a_t\)的出现概率\(p_\theta(a_t|s_t)\),但是当优化\(p_{\theta}(a_t|s_t)/p_{\theta^k}(a_t|s_t)\)小于\(1-\epsilon\)的时候,两个概率差异太大,不能继续优化,这个时候选择出来objective function直接变为\((1-\epsilon)A^{\theta^k}\)。
4. Actor-Critic方法
上一节介绍的纯policy learning方法都可以估计state value function,但是这些方法普遍存在两个问题:第一:更新policy的参数\(\mathbf{\theta}\)(尽管可以更新多次),需要完整的跑完任务。原因就是需要估计state value function中的action value function。这样运行时间消耗太大。第二:纯policy learning方法是基于采样的,非常不稳定:
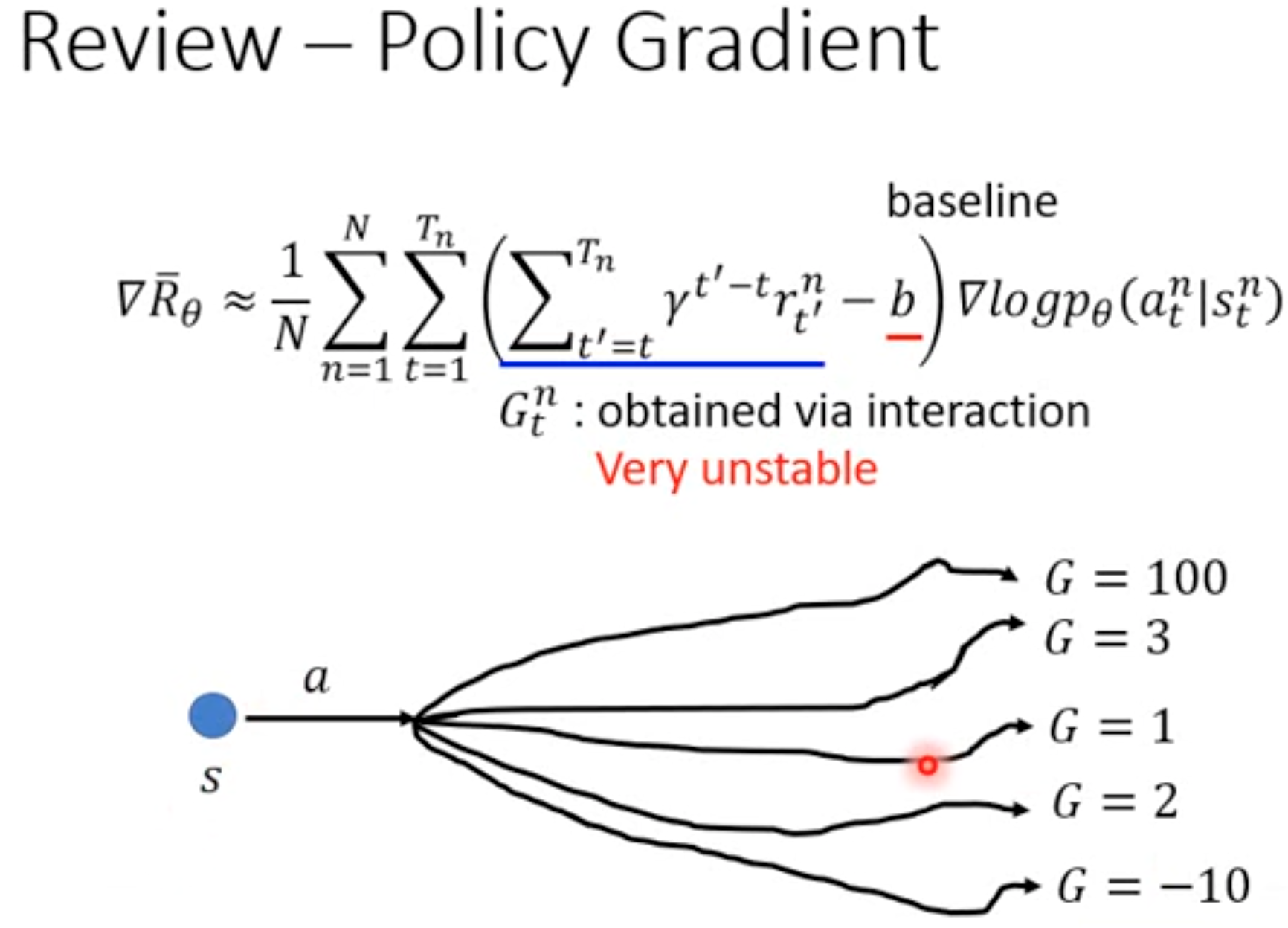
为了减轻这一负担,一个直接的想法就是能不能不需要完整的采样整个epside就可以估计action value。value learning就刚好可以用在这个地方。我们直接引入一个价值网络来估计action value function,这样只要每次policy输出新的action \(a_t\),动作价值网络就可以直接给出一个估计值,用来计算policy gradient。
actor-critic方法是同时使用价值学习与策略学习的方法,目的就是为了估计state value function,然后优化policy:
actor和critic的角色就类似GAN。actor要学会从critic里得到高value,critic要学会给出越来越准确的value估计。actor更新借助策略学习,critic更新借助价值学习。
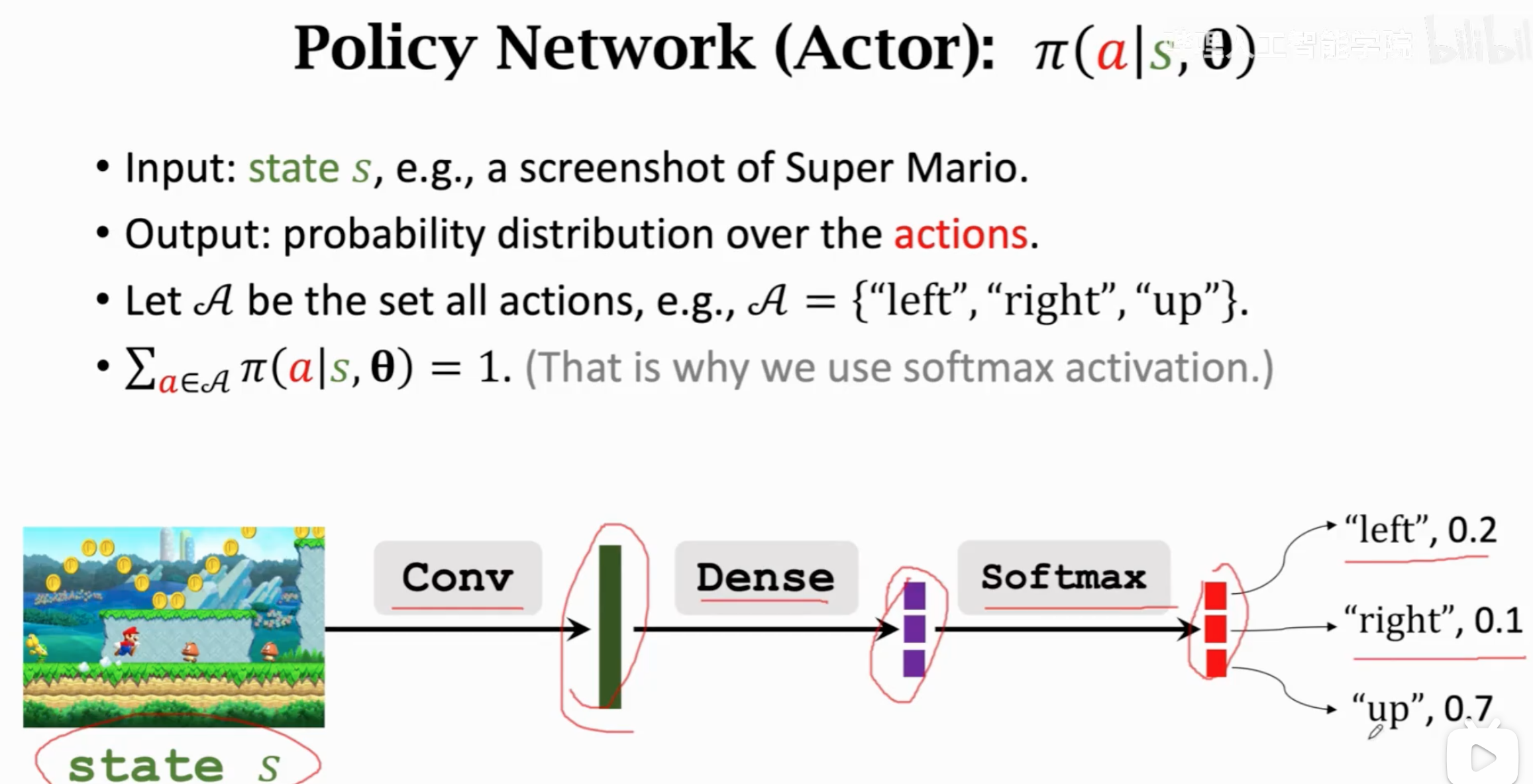
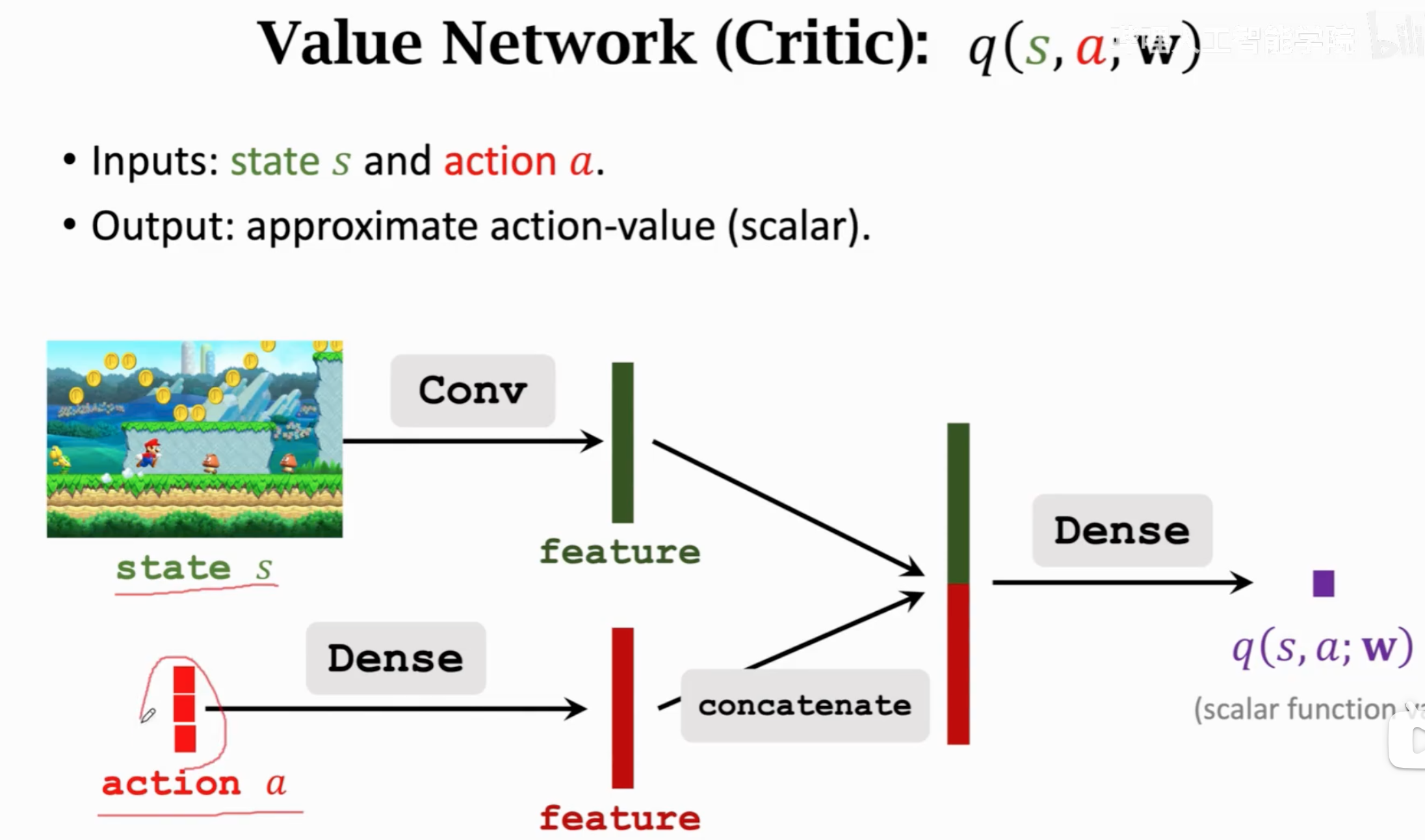


整个算法流程:

### SARSA
先用TD算法更新critic,再用策略学习更新actor。注意上面步骤里的第4步,随机采样\(a_{t+1}\)来估计了\(E_A(U_{t+1})\)。critic就是动作价值函数,它的优化过程就是借助TD优化算法类型的SARSA算法,下面是算法名称的由来:

SARSA算法的目的就是要得到\(Q_\pi(s_t,a_t)\)。它的第一个版本是对于动作范围和输入状态可能的组合固定的tabular version,它直接建立一个state-action的价值表格,计算TD target直接查询这个价值表格就可以:

下面的优化这个价值表格的方法,直接更新价值表格里面的值就好:

如果状态空间或者动作空间很大,那么这个价值表格就很大,很难学习。所以SARSA的第二个版本就是利用神经网络来模拟价值函数。

SARSA算法与Q-Learning算法的对比:


Advantage Actor-Critic
A2C就是带有baseline的actor-critic方法,需要计算advantage优势。advantage的计算需要估计baseline,似乎意味着需要用一个新的网络估计baseline,一个action value网络估计动作价值,一个policy网络决定动作。但这种做法是不必要的,因为如果我们将baseline选定为state value,action value和state value之间是存在联系的,action value可以被下一步的state value和当前的reward一起估计。这样我们还是只需要一个value network和一个policy network。只不过这个value network要估计的是state value。
A2C和一般的actor-critic的区别是训练的价值网络不再是估计action value function,而是估计state value function。
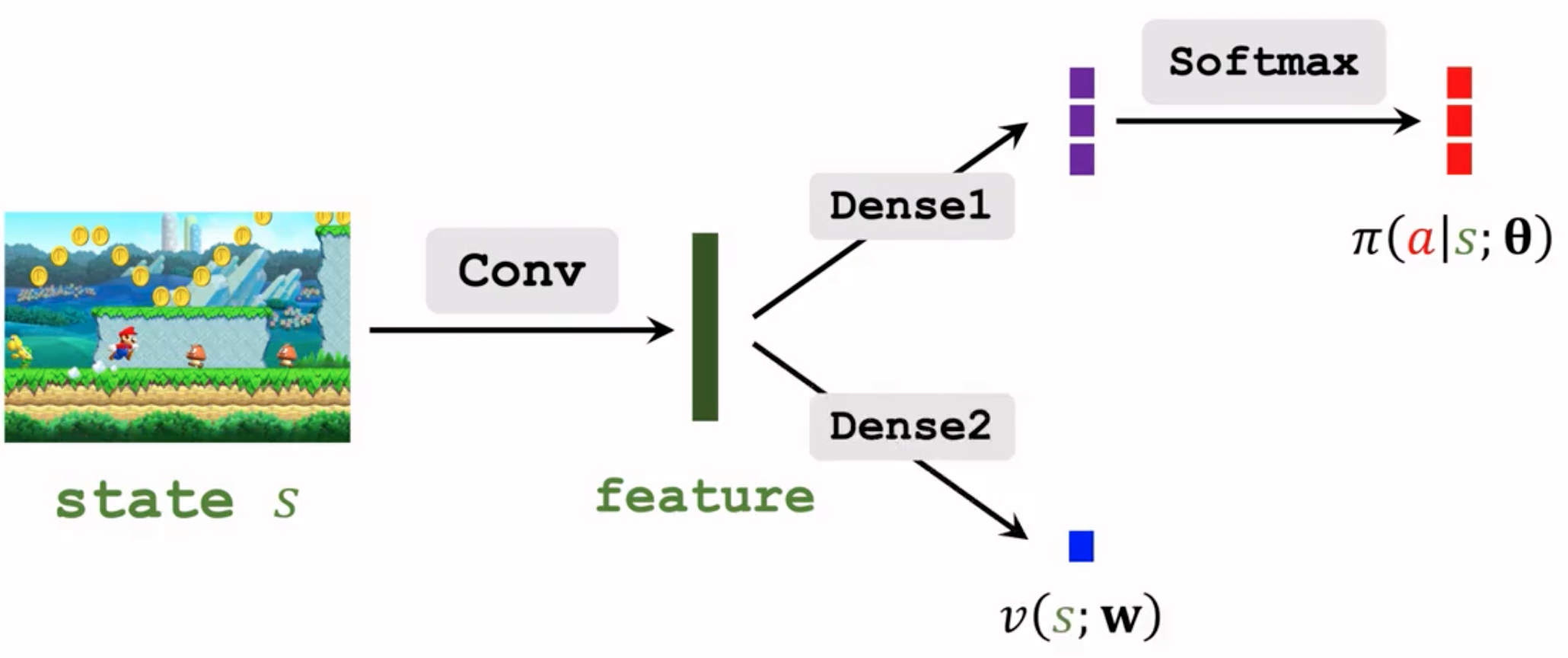
A2C的网络结构与一般的actor-critic不一样,因为它的value network不再是估计动作价值,不需要输入动作(即policy的输出),只需要输入state。这样,A2C的网络结构与带有baseline的REINFORCE方法一样:
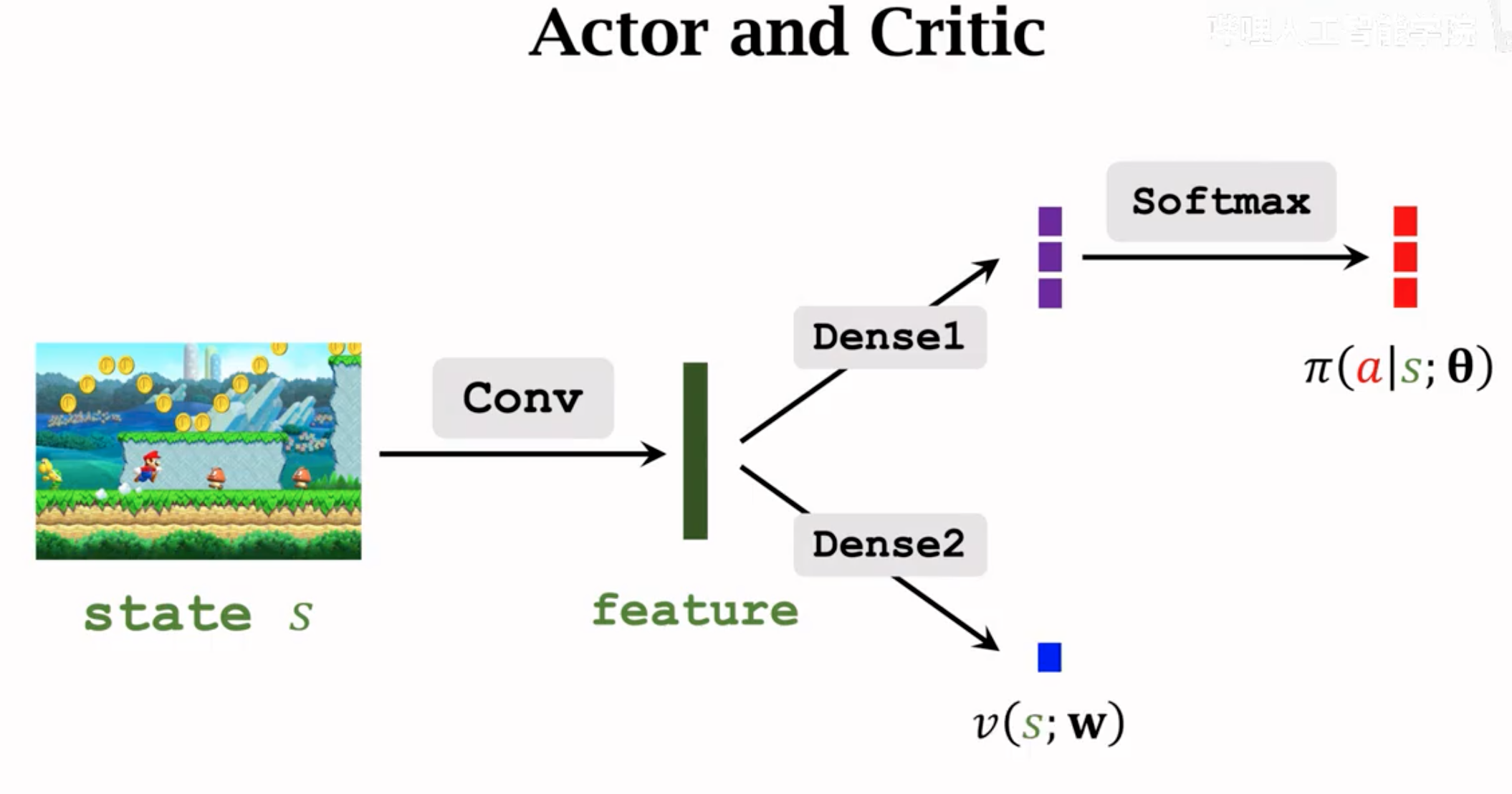
A2C的算法流程:

下面是具体的数学推导。我们对在TD算法中讨论过的action value的估计继续进行推导:

在原来的数学体系里,\(t\)时候的动作价值等于(奖励+下一步的动作价值)随着下一步的不同状态、不同动作概率的期望,而上面的推导过程发现,动作价值实质上等于(奖励+下一步状态价值)随着下一步的各个状态概率的期望。下一步的状态是不一定的,状态之间的转换可能存在概率。这里,动作价值和未来的状态价值建立了等式。
接下来,用上面的动作价值,计算当前的状态价值:

这里讲上一步的状态价值和下一步的状态价值建立了关联。
在拥有了上面两个定理之后,用这两个定义来更新policy network和value network。更新policy要计算带有baseline的policy gradient。在计算policy gradient的式子里,需要计算动作价值\(Q\),由于A2C里没有直接估计动作价值的value network,所以我们要使用能够估计下一步的state value的value network \(V_\pi()\)去计算动作价值\(Q_\pi()\):

用value network估计,然后计算policy gradient:

注意上面也出现了类似于TD target的\(y_t\),这不过这里的TD target既不同于SARSA算法(计算动作价值)也不同于Q-Learning算法(计算最优动作价值)。这里的TD是指计算两个状态价值之间的TD。更新value network需要使用TD算法:
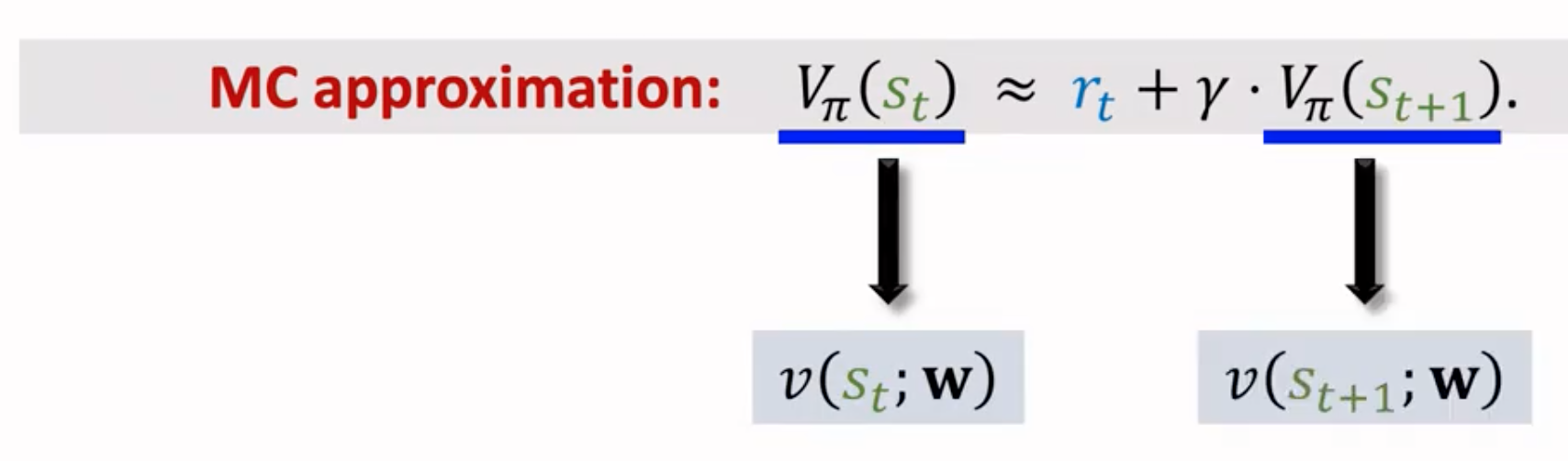

比较A2C和一般的actor-critic方法,他们的区别第一个是value network,A2C的value network输入是state,输出是state value实数;actor-critic的value network输入是state和action,输出是action value实数。第二个区别是,A2C计算的TD target是观察到的奖励+未来的状态价值估计,actor-critic的TD target是观察到的奖励+未来的动作价值估计。第三个区别是A2C不需要采样一个虚假的下一步动作\(a_{t+1}\),而actor-critic需要。第四个区别是A2C更新policy的时候,用到的公式和actor-critic不一样。A2C更新policy只需要TD error辅助,而actor-critic需要action value network估计的当前动作价值辅助。
接下来是一些理解。为什么A2C能够训练更好的policy \(\pi()\)?下面是A2C计算的策略梯度:

标蓝色框的项本质上是状态value network对于采用动作\(a_t\)好坏的一个评估判断。

红色框是在没有采取动作\(a_t\)之前的状态价值估计,代表当前局势\(s_{t}\)的好坏。

紫色框是采取了动作\(a_t\)之后的状态价值估计,它代表采取动作\(a_t\)之后,再回过头来评价局势\(s_{t}\)的好坏。两者都是在估计当前状态,两者的差就能够代表采取动作\(a_t\)之后对于局势的改变,动作越好,\(v(s_{t+1})\)越大,奖励越大,这一项值越大,反之,这一项值越小:

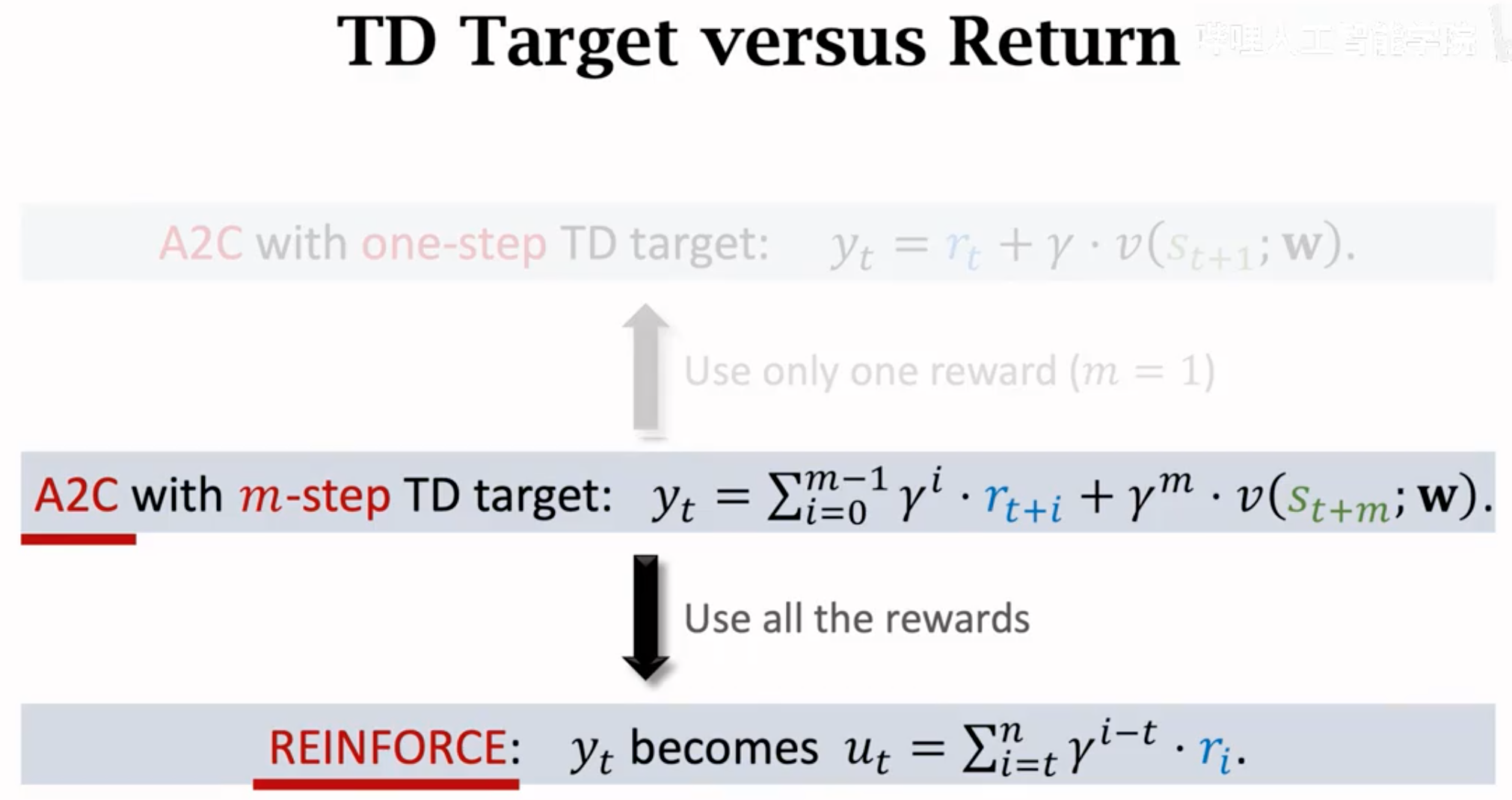
我们还可以进一步用multi-step TD来改进A2C,这也是使用A2C的时候真正会使用的计算TD target的方法。改进很简单就是在计算TD target的时候,使用多个观察到的奖励。假设使用\(m\)步的观察到的奖励:


然后我们可以比较一下A2C和REINFORCE with baseline。两者的网络架构设计完全一样。但是value network的作用不一样。REINFORCE的value network只是作为baseline来加速收敛,而A2C的value network需要评估policy的好坏。下面的REINFORCE with baseline的优化过程,它需要完整的跑完整个任务到终止。所以能够观察到完整的回报return也就是累积奖励。不需要计算TD target。
REINFORCE实质是A2C的一种特例。如果A2C计算TD target的时候,直接使用从现在到任务终止的所有奖励,那么它就变成了REINFORCE。A2C消除掉bootstrapping就是REINFORCE。

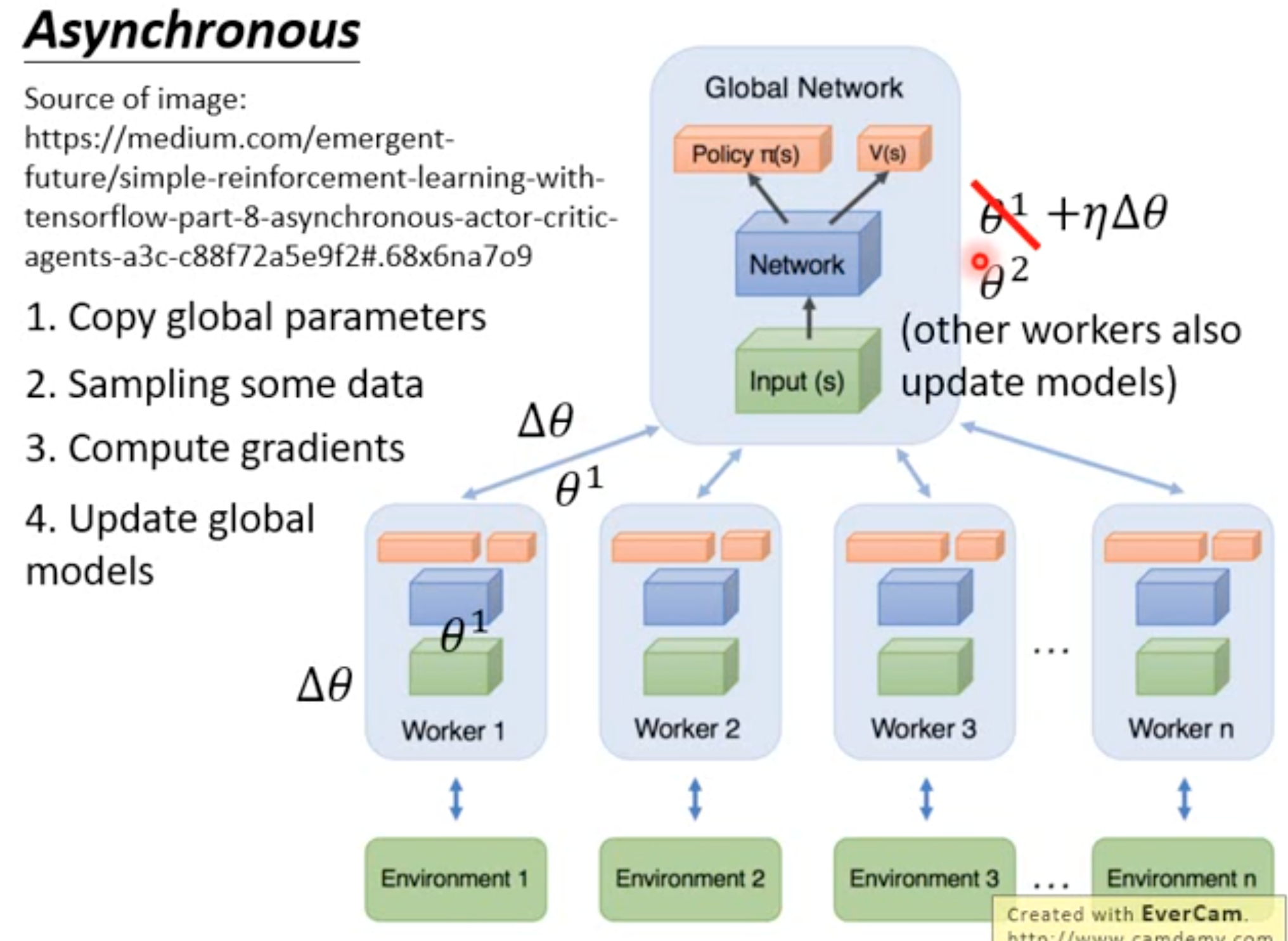
A3C就是带有异步学习的A2C:
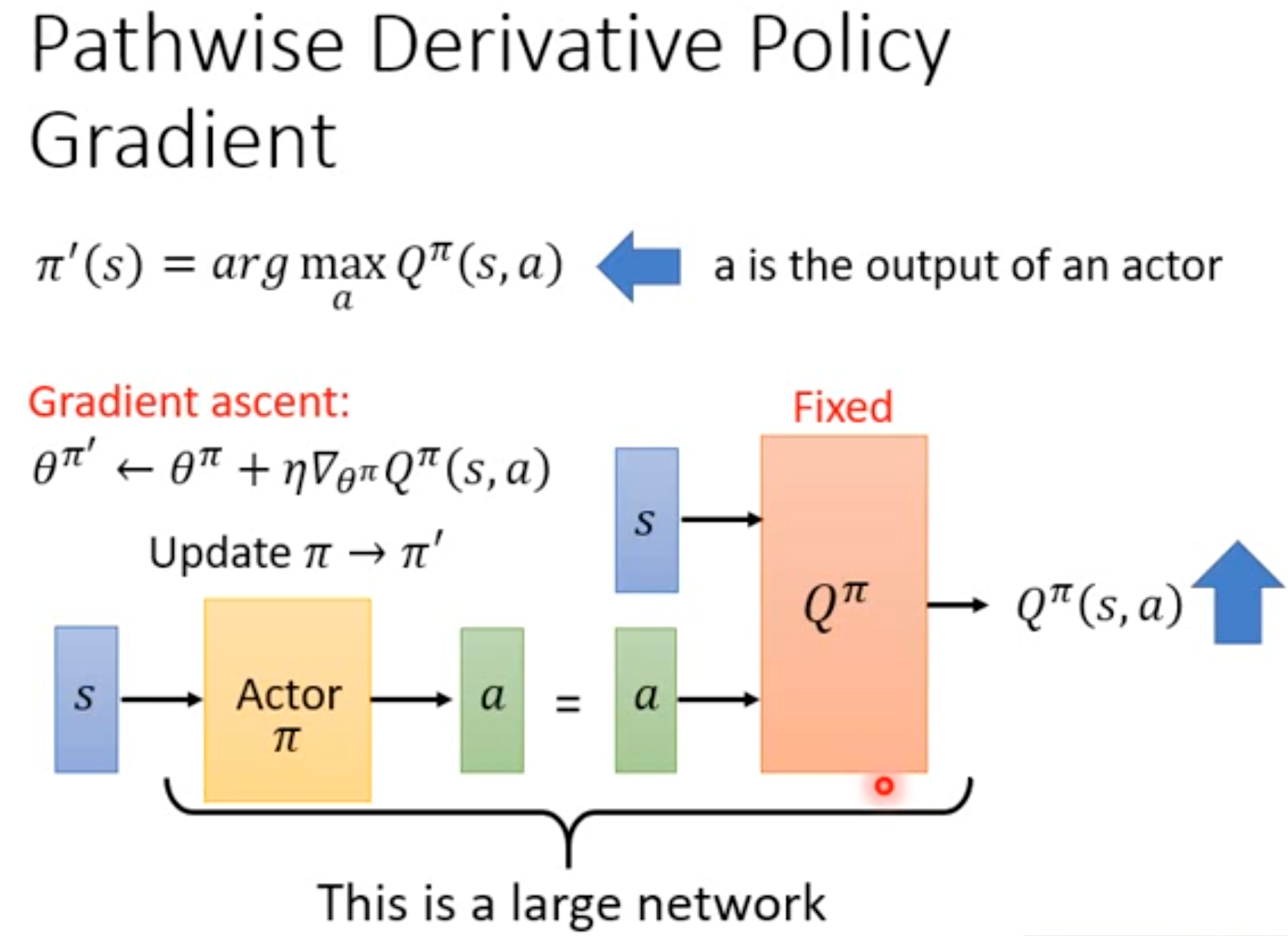
Pathwise Derivative Actor-Critic
一般的actor-critic中的critic只负责评估在当前状态下采取当前的action的value(因为采取某个action只会对应一个估计的value),而没有告诉actor在当前状态下如果采取其它的动作是不是能有更好的value。Pathwise Derivative Actor-Critic非常类似GAN,actor负责输出能够让critic最大的action,critic负责评估这个action的value。在同一个状态下,critic能够评估actor的不同动作的value。它也是一种能够让Q-learning解决continuous action的方法(选择最大动作的时候不依赖argmax操作,而是直接就利用actor输出的action)。
Pathwise Derivative Actor-Critic的网络结构不再是policy和value共享参数,而是policy的输出作为critic的输入,两者联合起来作为一个network:
下面是算法流程:


Deterministic Policy Gradient
上面提到的方法都没有讨论过如何处理连续动作的问题。例如一个机械臂的转动角度,是一个多维的向量(每个关节有一个角度实数)。前面的方法value leaning通过估计特定动作的价值选择最佳动作,而policy输出的是不同动作概率(是一种随机policy),这都需要动作空间是离散的。对于连续动作需要有特殊的处理。
对于policy network来说,输入状态,输出是确定的动作向量,不能够再进行基于概率的抽样,这就是deterministic policy确定性policy。下面的结构就类似于上面的pathwise derivative actor-critic。
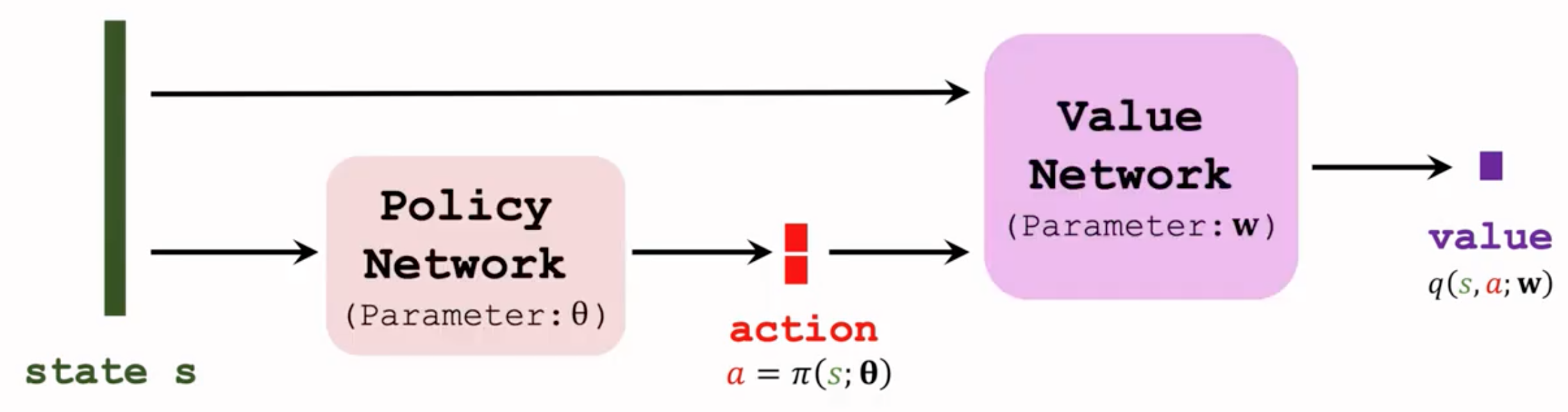
更新value network使用TD算法:

更新policy network参数,希望的是policy输出的动作能够让critic(冻结)的结果变大:

对于DPG还有不同的改进,例如引入target network估计\(t+1\)时候的奖励;引入experience replay等。

实例分析:AlphaGo
整体训练预测流程:

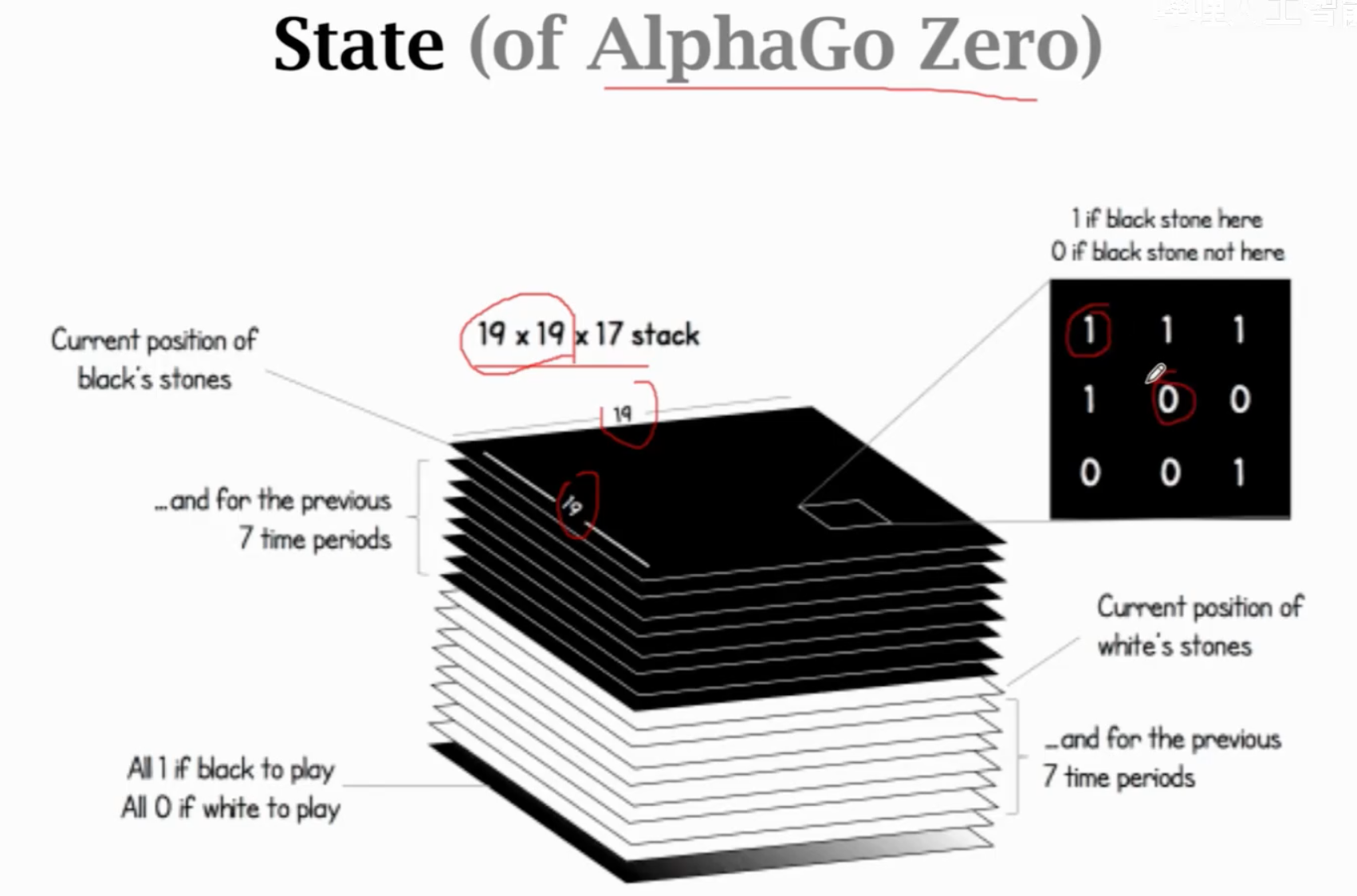
AlphaGo zero的state是19x19x17的张量(8个矩阵代表黑子在前7局的落子和当前局的落子,在哪里有黑子就是1,否则都是0;8个矩阵代表白子在前7局的落子和当前局的落子;还有一个矩阵全是1代表当前落黑子,全是0代表当前落白子)。
policy network的设计:
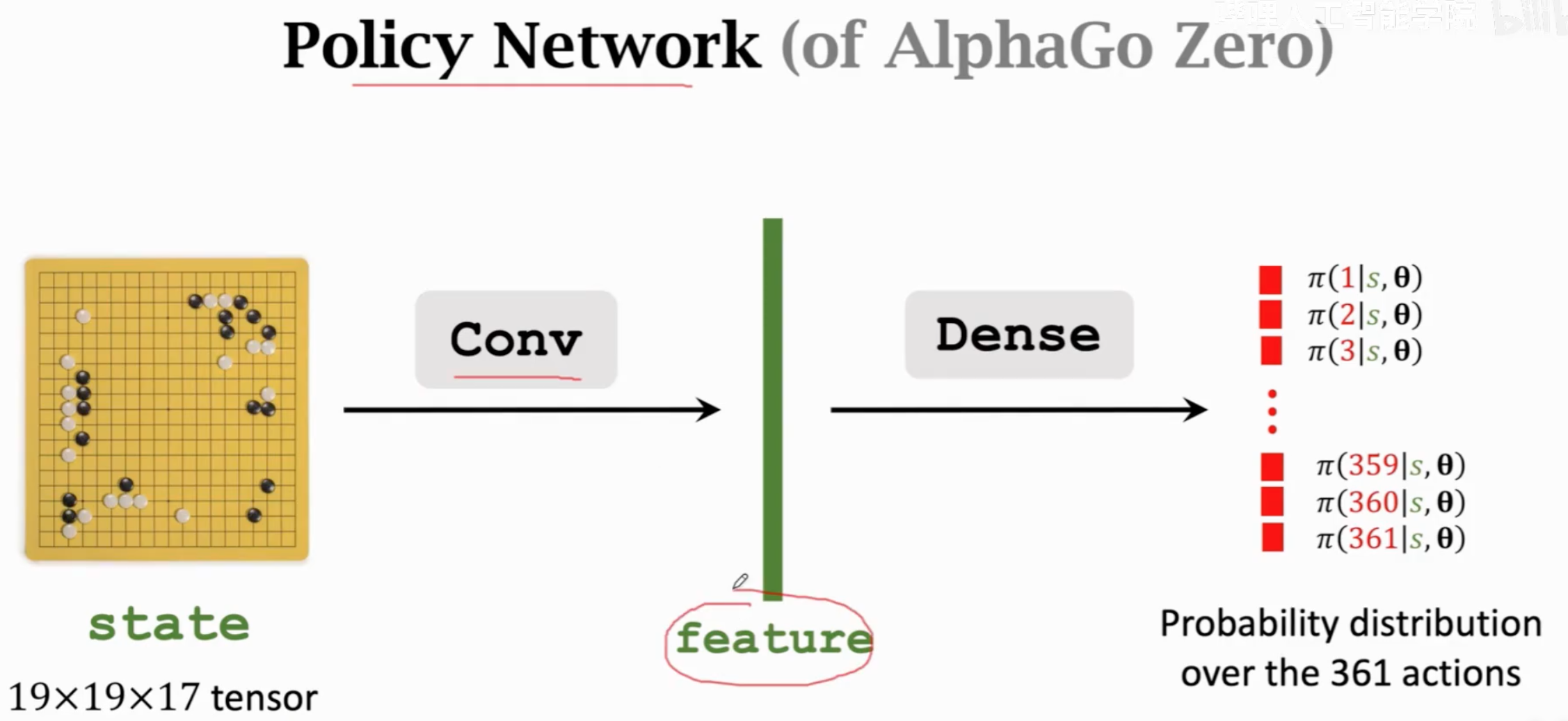
AlphaGo先用监督学习,从16万局人类棋盘的数据中微调一个具备一定下棋能力的policy network。
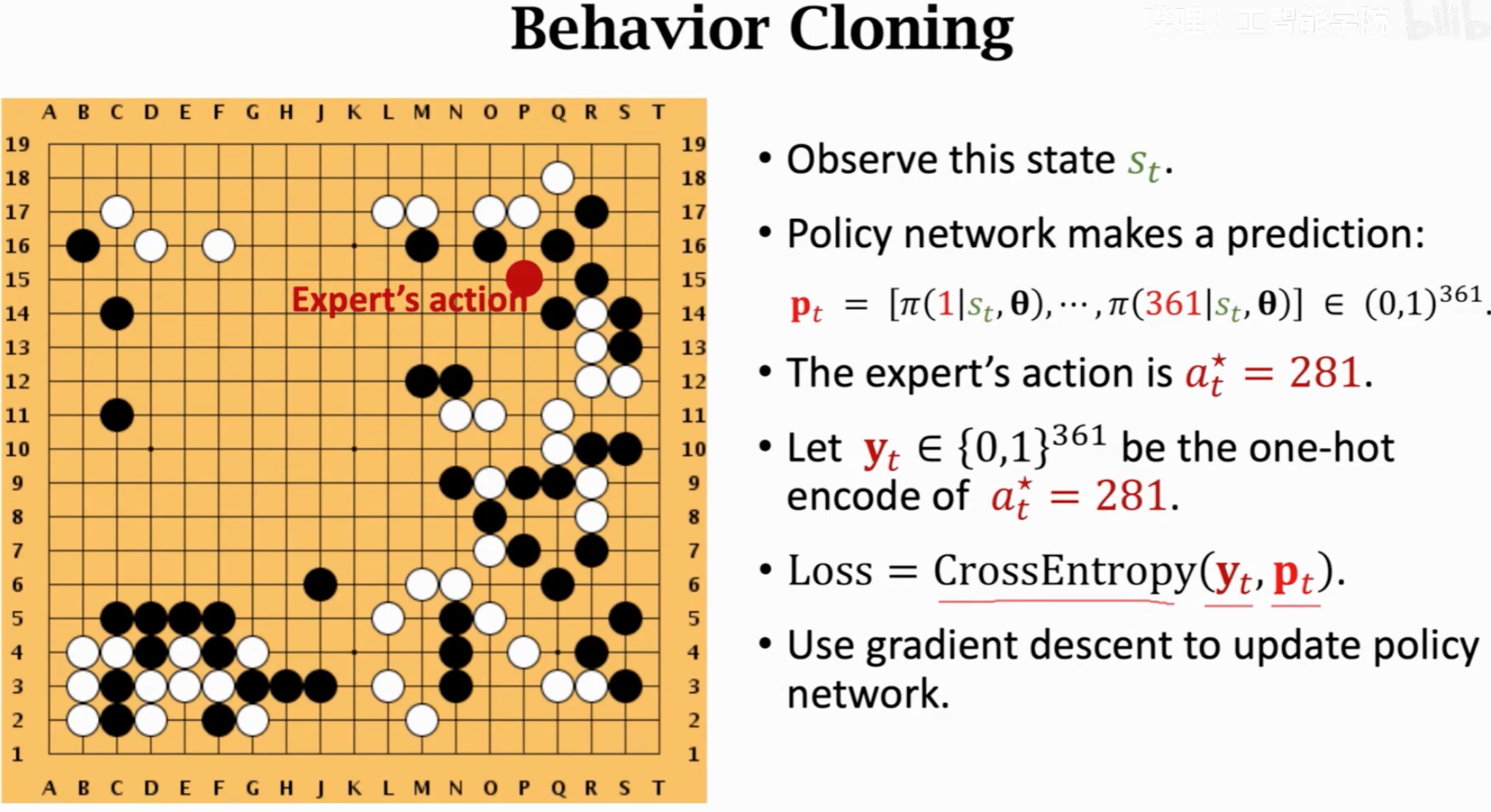
然后第二阶段,自己和之前的自己下棋,借助RL让policy学会自己根据不同的state去决策,而不是仅仅只能应对前一阶段见过的state:

奖励的设置就是最后赢了(\(+1\))还是输了(\(-1\)),中间每一步的奖励是0,那么累积奖励要么都是\(1\)要么都是\(-1\)。因为只有最后一步才有奖励,所以没有discount factor。

计算策略梯度用于更新policy player:

上面是REINFORCE的方法。
第三个阶段是借助于训练好的policy network,训练一个价值网络。但是和一般的DQN( \(Q^\star(s_t,a_t)\))和actor-critic方法(\(Q_{\pi}(s_t,a_t)\))里的value network估计的是action value function不同,这里的价值网络是直接估计state value function \(V_\pi(s_t)\),评估当前局势的好坏。

在AlphaGo zero中,value network的设计:
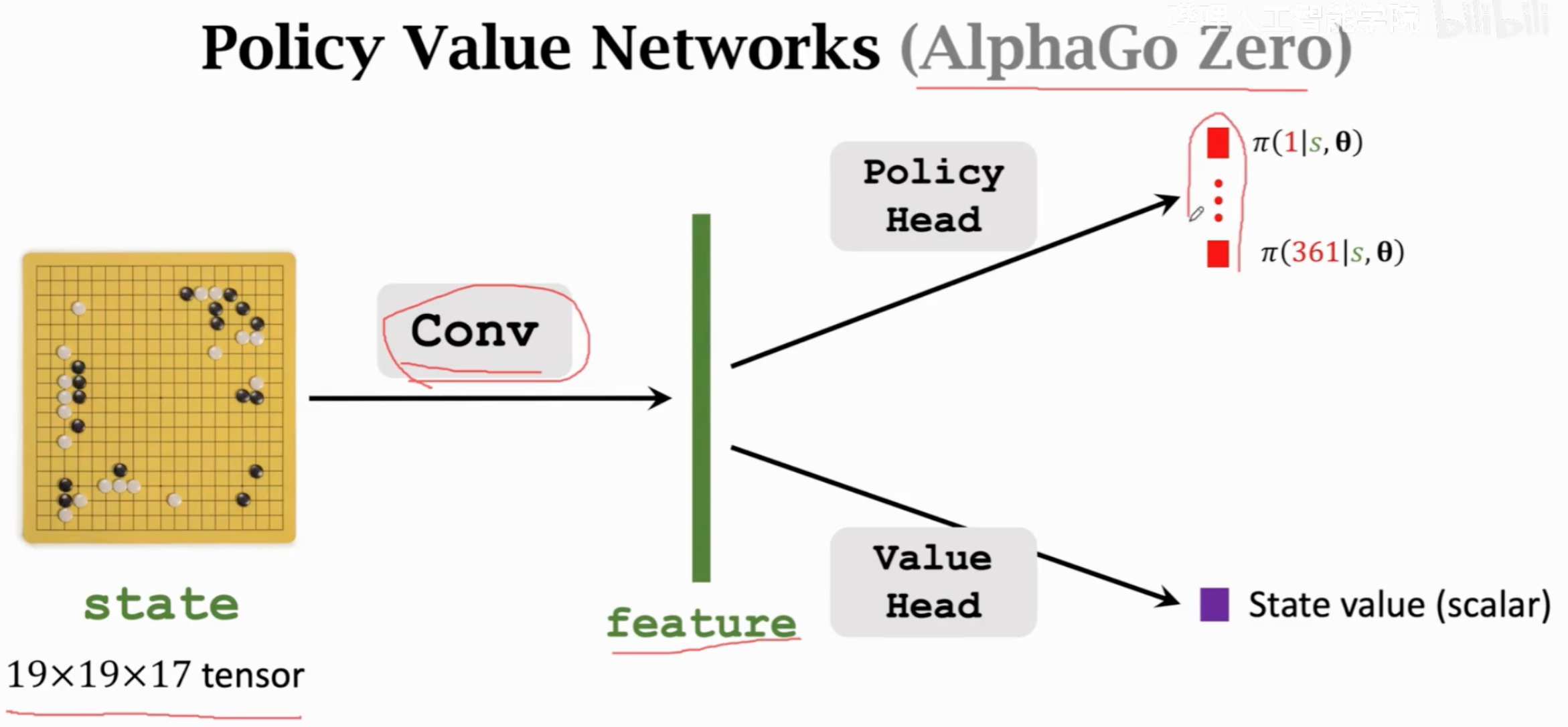
它的训练过程就是一个回归任务:

训练阶段结束之后,就是真正的开始和人下棋,inference阶段。在这一阶段,不是单纯的依靠policy或value network来进行,而是用policy和value network辅助蒙特卡洛树搜索。
蒙特卡洛树搜索有四步,每一步在有policy和value network的帮助下能够更有效率的执行:

第一步是选择某个动作,选择的依据是综合考虑policy的决策和一个动作价值得分\(Q(\cdot)\)(初始化为0)。选择综合得分最高的那个。一开始的时候,主要根据policy进行选择,后来随着选择次数\(N(a)\)的增加,而主要根据动作价值\(Q(a)\)进行选择。

第二步是拓展,借助policy估计如果是对手的话,可能的落子是在哪里:

第三步是评估,用policy自己和自己下,直到最终比赛结束获得奖励。同时也直接用value network估计当前的局势。
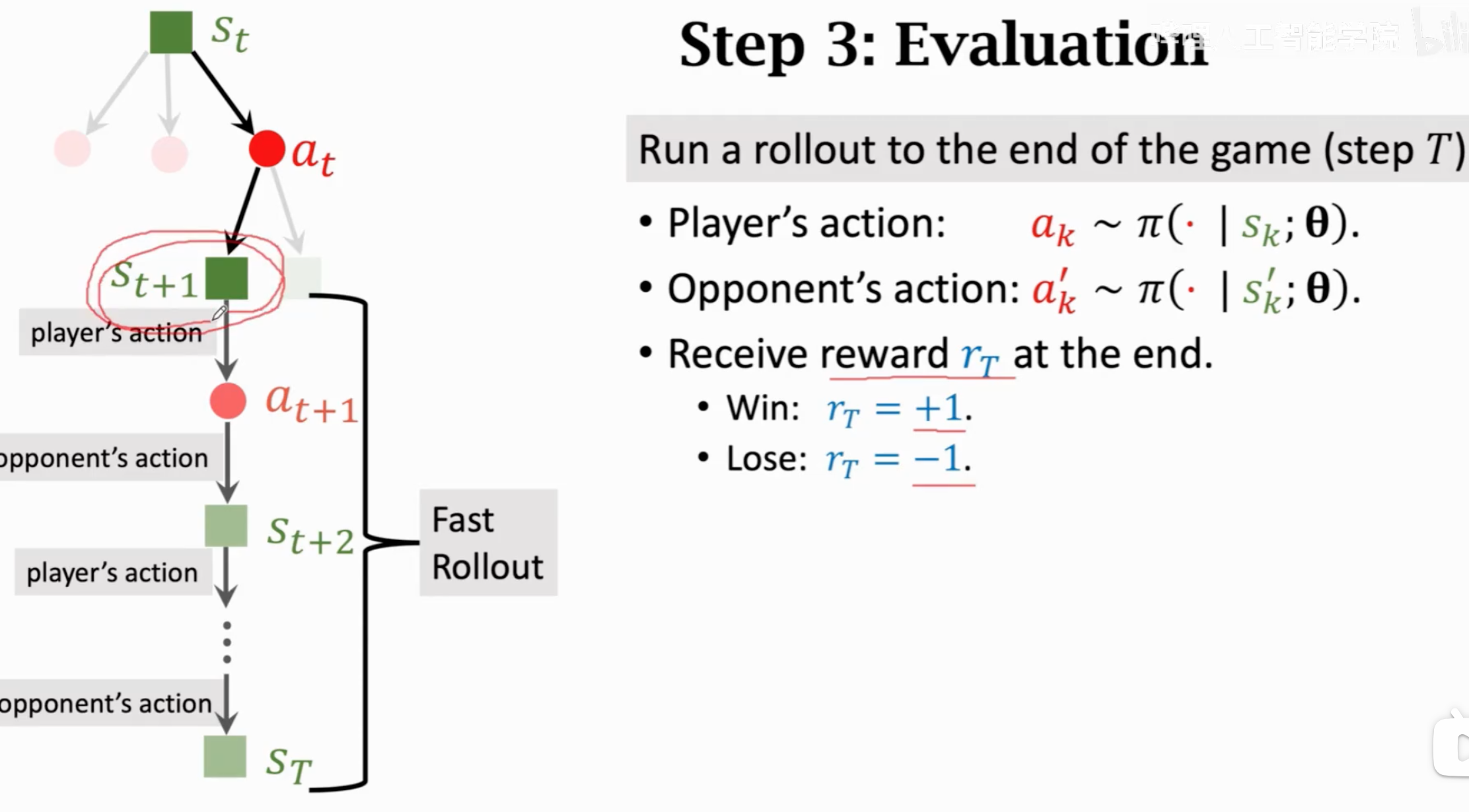

第四步是回溯,根据第三步的奖励和价值,更新动作价值得分\(Q\):
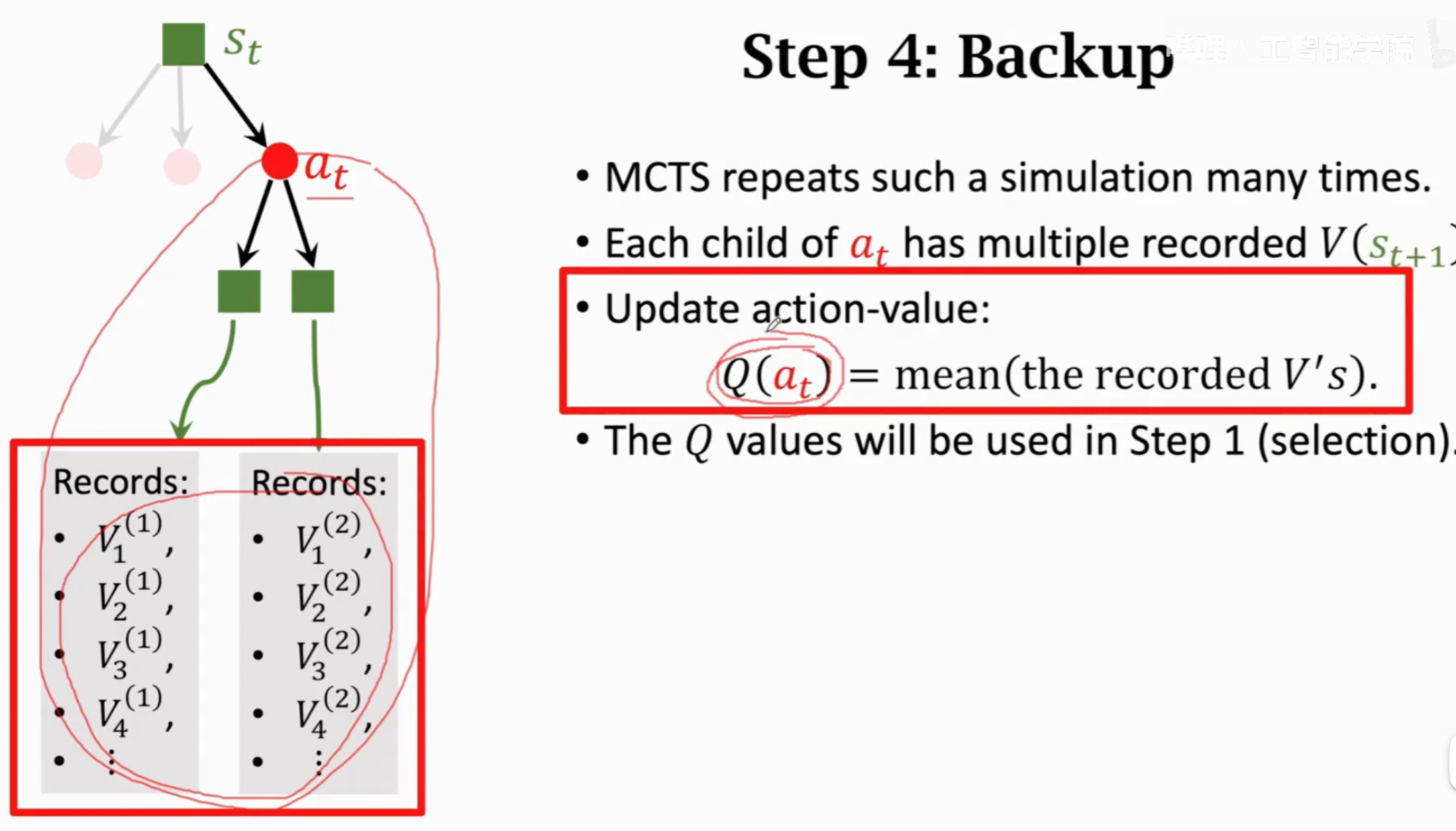
前面四步重复成千上万次,选择被选中次数最多的那个动作作为真正的下一步动作:

人类对手下完一步之后,所有动作价值和动作访问次数等都重置,继续重复四步动作。
AlphaGo zero与老版本的对比:

取消了模仿人类数据学习;直接利用蒙特卡洛树搜索的结果作为annotation,让policy去模拟。
5. 蒙特卡洛方法
蒙特卡洛方法是一类用重复随机抽样来估计真实值的方法,有着广泛的应用。“蒙特卡洛”这个名词是一个著名赌场,这个方法是由metropolis在1947年提出的。

蒙特卡洛方法的结果总是错误的,但是它能够非常接近真实值。这在机器学习内就已经足够用了。除了蒙特卡洛方法还有很多随机算法,他们往往都喜欢用赌场来命名:

其背后的原理是大数定理,即随着抽样次数的增加,样本的平均值会逼近期望。

蒙特卡洛方法可以用来估计圆\(\pi\)值,用投点法或者是投针法都行。投点法就是假设一个正方形和一个与正方形内部正切的圆,一个随机出现在正方形内的点出现在内部圆这一事件发生的概率期望是\(\pi r^2/r^2\)。随机实验\(n\)次,观察到有\(m\)次落在圆内,观察到的事件发生的平均值也就是频率为\(m/n\)。根据大数定律,\(m/n \rightarrow \pi r^2/r^2\)。并且\(n\)越大,误差上界越小。
蒙特卡洛方法的最重要应用之一就是估计积分。

在上面的例子中,假设\(f(x)\)的期望是\(E(f(x))\),则它\(n\)次随机采样的平均\(1/n \sum_nf(x)\)可以毕竟这个期望: \[ \frac{1}{n}\sum_n f(x) \rightarrow E(f(x)) \\ E(f(x)) = \frac{\int_a^b f(x)dx}{b-a} \\ (b-a) \frac{1}{n}\sum_n f(x) \rightarrow \int f(x)dx \] 上面公式的第二步可以直观的理解是把一个函数曲线下的面积,捏造成一个面积同样大的高度为\(E(f(x))\),宽度为\(b-a\)的矩形。
对多元函数求积分:

输入的变量是一个向量,向量的可取值范围是一个集合,需要在第2步求\(\Omega\)的体积。求体积的过程是一个函数值始终为\(1\)的函数求积分。这个过程可能很复杂,所以需要\(\Omega\)是一个简单的可以便于求导的集合。在这一步,我们没法再嵌套使用蒙特卡洛方法估计。因为试想一下 \[ 1/n\sum_n1 \rightarrow E(1)=1=\int_\Omega 1/\Omega \] \(\Omega\)根本就解不出来,左边的抽样求平均始终是1,右边函数的期望也始终是1,这是一个1=1的问题,没有其它变量能够用来估计\(\Omega\)。所以,我们只能要求\(\Omega\)是一个简单的便于求导的集合。
在上面求积分的过程中,我们假设抽样在输入区间内是完全等概率随机的。但是输入的变量完全可能是某个概率,这时我们只需要随机抽样的时候按照符合输入概率进行抽样即可。下面是用蒙特卡洛来估计期望的一般方法:

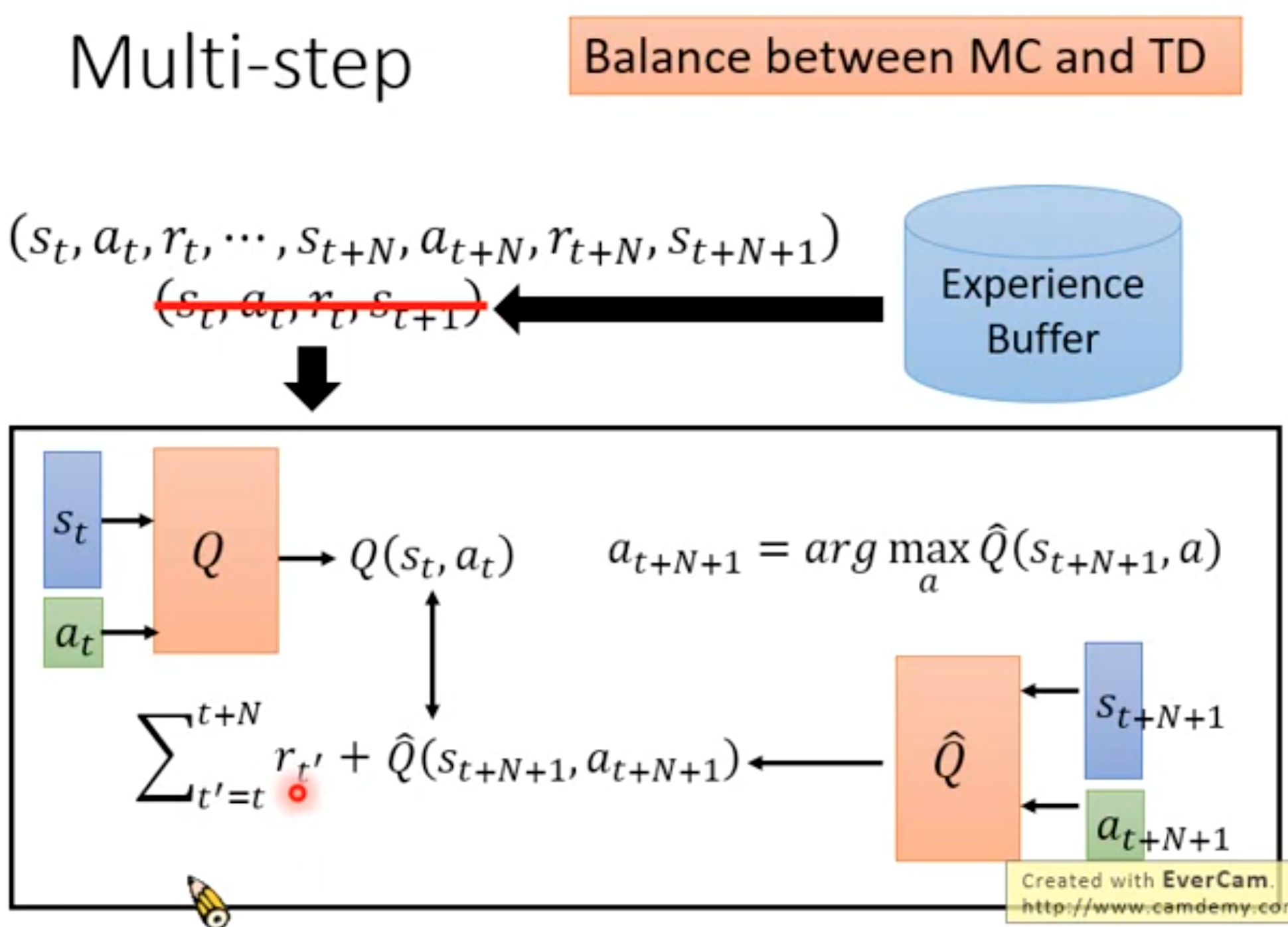
6. Multi-step TD
上面在学习DQN的optimal value function以及actor-critic中的action value function的时候用到了Q-Learning和SARSA算法。它们最原始的版本是只使用了当前一步的奖励来计算TD target。实际上,我们完全可以等待观测多步的奖励,然后来计算TD target。这就是multi-step TD。
multi-step TD由于使用了更多的观测值,效果往往更好(可参考Rainbow的paper)。下面是推导过程:

不断的把未来步的奖励展开。如果将SARSA算法改为使用multi-step TD:

如果将Q-learning算法改为multi-step TD:

Multi-Agent
多个智能体在同一个环境中,有下面几种模式:
智能体的奖励目标一致:

智能体的奖励完全相反:

部分智能体目标一致,部分相反:

每个智能体只关注自己的奖励,对其它智能体的影响可能是好也可能是坏:
自动驾驶就是self-interested的。
一些基本概念,状态转移与所有智能体的动作有关;每个智能体能够获得的奖励也会被其它智能体的动作影响;


因为奖励和所有agent的动作都相关,因此每个agent的状态价值函数都会和所有agent有关。比如一个守门员agent的参数变化,会直接引起其它所有踢球agent的状态价值变化。

在单个agent的情况下的收敛是指polity的状态价值(累积奖励期望)不再增加:

多个agent的收敛是指达到了纳什均衡:在其它agent不改变的情况下,仅仅是改变自身agent参数不能够让奖励期望更大。

多智能体强化学习的难点就在于如何找到这个纳什均衡。因为试想一下,每个agent的改变,都会引起其它agent的奖励期望发生变化,其它agent就会继续改变自身的参数,又使得当前agent需要进行改变。


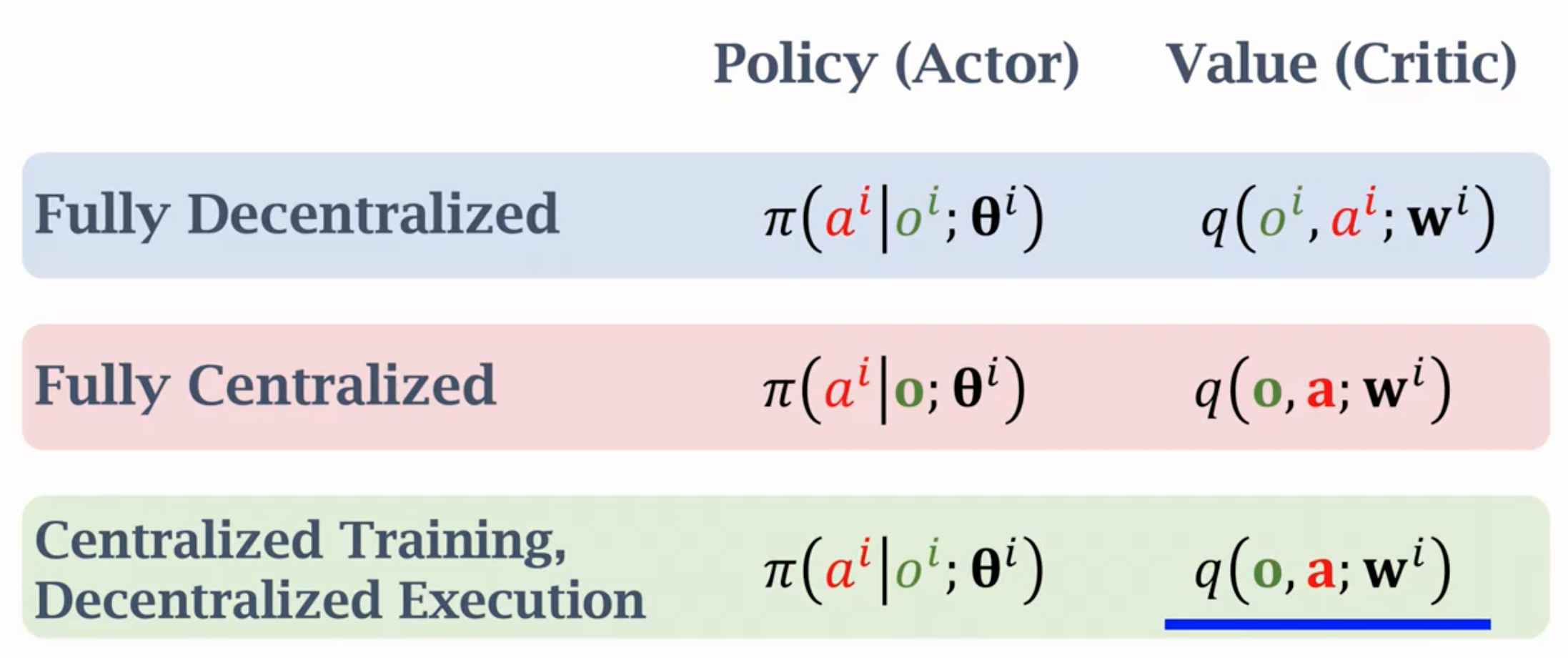
不能直接把单智能体的优化算法直接引用到多智能体上。也就是说,需要让智能体之间做通信。实际上,每个agent不一定能够看到整体的全部state,只能有部分的观测值:

一个方案是设置一个全局controller,可以收集所有agent的state,并且为每个agent学习policy network和value network。controller做好决策之后,再把选择好的动作传回到各个agent上。
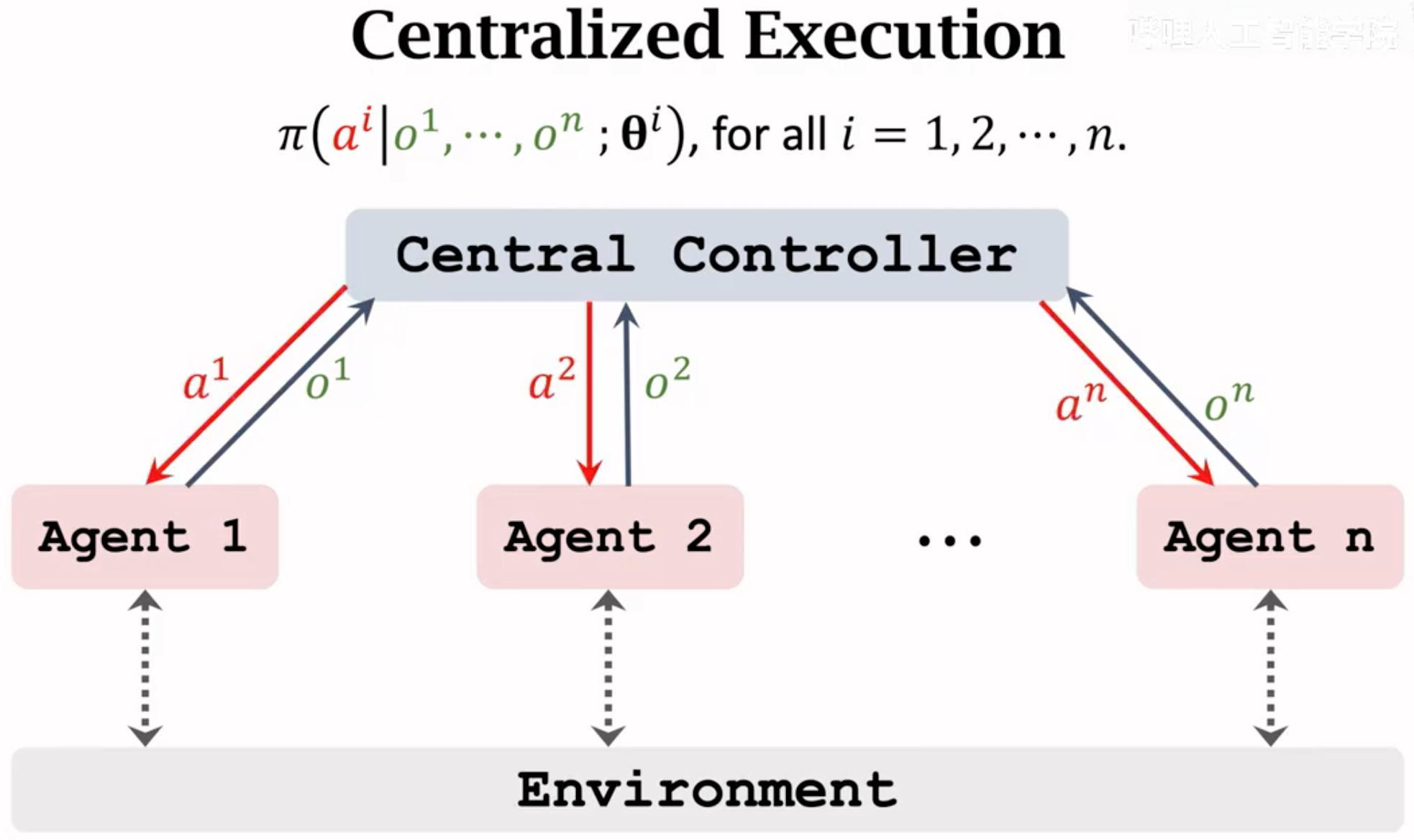


上面这种做法的缺点是效率低,controller做决策需要等待同步传输最慢的那个agent的状态。另一个做法是训练时使用集中controller,但是inference的时候,每个agent有自己的policy,不需要等待其它agent就能够独立的做出决定:

也就是controller里有能够接收全局state的value network,但是这个value network只是用来辅助训练各个agent的policy network。policy不需要全局state,而是只需要局部观测就能够做出决策。
对应不同agent的policy network和value network之间可以共享参数: