ONN
1 背景
ONN(Operation-aware Neural Networks for user response)是2018年腾讯广告算法比赛最优的推荐算法。主要任务是预测用户点击推荐广告的概率(click-through rate, CTR)或者进行其它期望的行为(conversion rate, CVR)。在基本的通用的Base model上,将PNN与FFM结合起来,实现了在embedding层的每一个feature对于不同operation(内积或者外积)有不同的表示,之后进入MLP,得到更好的预测结果
2 创新点
2.1 针对的问题
目前的大多数的模型对于一个feature上的embedding vector进行不同的operation都是使用相同的表示。但是对于不同的操作,一个feature的最好表示不总是相同的(Juan et al., 2016; Rendle & Schmidt-Thieme, 2010)
2.2 解决思路
在基本的通用的Base model上,将PNN与FFM结合起来,实现了在embedding层的每一个feature对于不同operation(内积或者外积)有不同的表示,之后进入MLP,得到更好的预测结果
3. 相关的模型
3.1 FFM
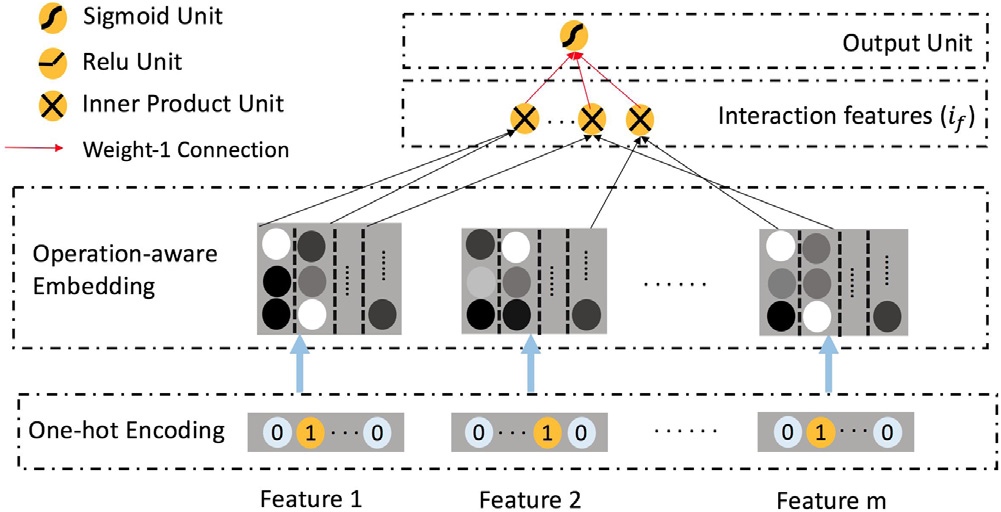
3.2 Base Model
深度学习引入推荐系统之后,深度学习的优势在于可以获取到特征的高维信息,一般的过程可以概括成以下三步:
- 一个embedding layer,负责将离散的feature映射到更低维的表示形式。
- 对于一个样本的特征表示为\(f=[x_0, x_1, \ldots x_m]\)
- embedding矩阵表示为\(M = [V^0, V^1, \ldots V^m]\)
- 两者作积得到的这一步的输出概括为: \[ e = [V^0x_0, V^1x_1, \ldots V^mx_m] \]
其中的\(V^i\)是中对应\(i\)th feature的那一列,\(x_i\)是\(i\)th feature的one hot表示。
- 对于上一步得到的结果进行operation,这一步可以表示为\(f = [o_1(e), o_2(e), \ldots o_l(e)]\),\(o_i\)是表示\(i\)th operation,这个operation可以是两个向量内积或者外积,在多数的结构中,这个操作只是一个copy操作,暨不进行任何的操作。这种在embedding向量上进行的操作可以看成是一种初期的特种工程。
- 第二步得到的结果输入MLP(multi-layer perceptron),最终输出\(\hat{y} = \sigma(\Phi(f))\),\(\sigma\)是sigmoid函数,\(\Phi\)是MLP的非线性转换
3.3 PNN
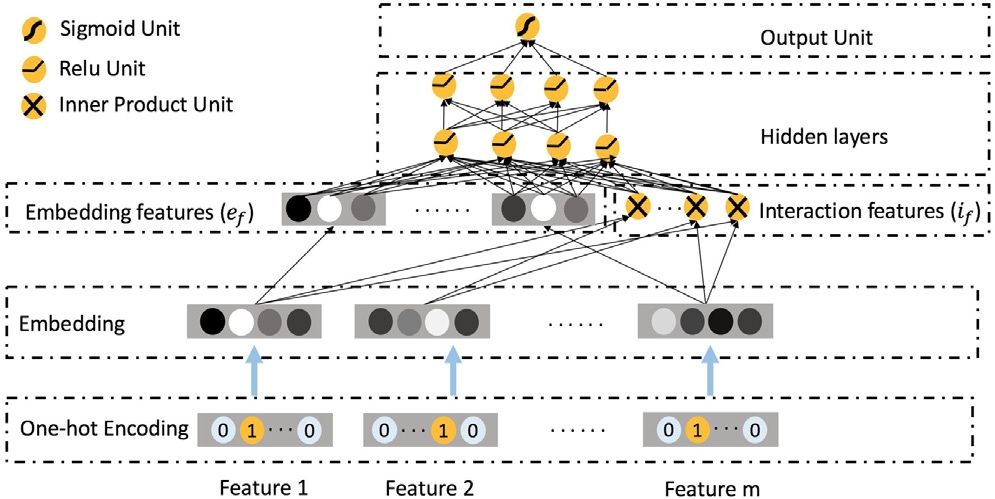
4 ONN结构
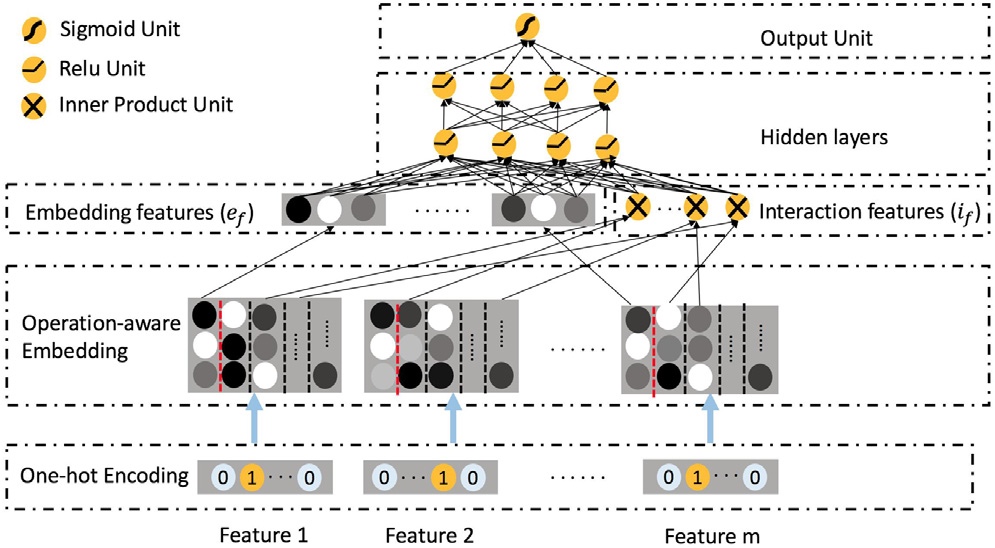
可以看到最大的特点在于对于\(i\)th feature的one-hot表示转换为embedding后拥有多个表示,在进行不同的operation时,采取了不同的表示形式。
4.1 Operation-aware embedding
下面说一下对于\(i\)th feature的具体转换过程。 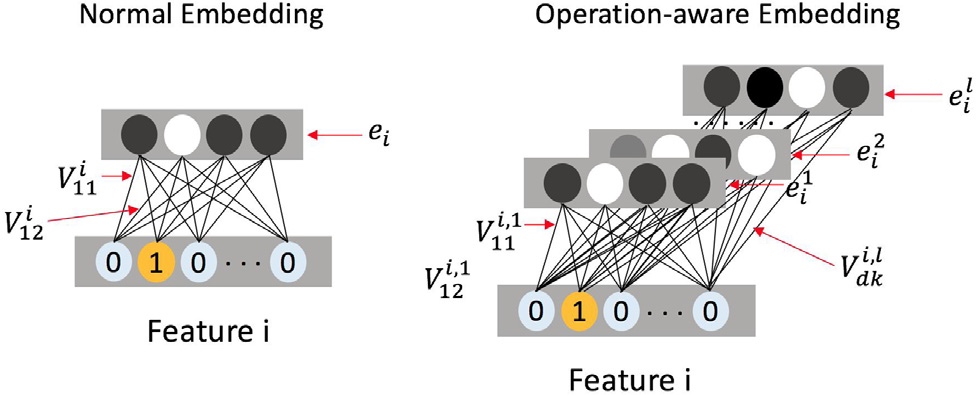
在上图的左边部分中,\(e_i\)是feature的转换后的embedding,\(V^i\)代表对应\(i\)th feature的embedding matrix,这样得到的\(e_i\)就只会有一种表示。
而在ONN改进后的右边部分中,设置了\([V^{i,l}, V^{i,l}, \ldots V^{i,l}]\),其中的\(V^{i,l}\)表示对于\(i\)th feature的\(l\)项操作。这里要注意的是同一种操作比如求内积,\(i\)和\(j\) 求内积与 \(i\)和\(p\) 求内积是不一样的操作。 最终的到的\(e_i\)就是一个矩阵,\([e^1_i, e^2_i, \dots, e^l_i]=[V^{i,l}x_i, V^{i,l}x_i, \ldots V^{i,l}x_i]\),在进行\(k\)项操作时,取出\(e^k_i\)表示进行操作。 为了表示在\(i\)th feature上进行操作\(o\)时要使用的\(k\)表示定义为:\(\Gamma(o, i)=k\)
在实现当中,实际求内积只在用户特征和推荐广告的特征之间进行,
4.2 Incipient feature extraction layer
在上一个的基础上,来看一下对于一个样例 \(f\)的最终输出形式是什么。 \[ f = [e_f, i_f] \] 其中第一项\(e_f\)是\(f\)的所有特征的embedding vector,表示为: \[ e_f=[e_1^{\Gamma(o(c, 1), 1)}, e_2^{\Gamma(o(c, 2), 2)}, \dots, e_m^{\Gamma(o(c, m), m)}] \]
公式中的\(o(c, i)\)是指对\(i\)th feature进行copy操作 第二项\(i_f\)是表示feature interactions,具体的说是两个feature embedding vector的内积。只求两个向量间的内积是再多的就过于复杂,求内积是在之前的实验中证明了内积效果比外积要好(Qu et al., 2016)。公式为: \[ i_f=[p_{1, 2}, p_{1, 3}, \dots, p_{m-1, m}] \] \(p_{i, j}\)是指在\(i\)th feature和\(j\)th feature之间求内积,\(p_{i, j}=\big \langle e_i^{\Gamma(o(p, i, j), i)}, e_j^{\Gamma(o(p, i, j), j)} \big \rangle\)
4.3 MLP
两个hidden layer,最后一个sigmoid输出 两个hidden layer的输出表示为: \[ l_1=BN(relu(W_1\hat{f}+b_1)) \] loss函数是交叉熵
5 与其它模型(PNN, FFM)的关系
- 回顾一下PNN模型的结构,和ONN的主要区别在于embedding layer,ONN实现了operation aware,即一个feature有了多种embedding vector,这样对于不同操作可以选择不同的feature表示。这样在训练时就得到了更好的特征表示。
- 和FFM模型最大的区别在于ONN加入了MLP,加入了深层网络后,深度网络能够更好的挖掘特征深层次的依赖,能够学习到复杂的特征依赖关系
6 实验
6.1 数据集
- Criteo: 包含45million条用户点击广告的记录,使用了最后5million作为测试集(8:1),数据集中包括13个连续特征和26个分类特征。通过\(discrete(x)=\lfloor 2 \times log(x) \rfloor\)将连续量离散化
- 腾讯广告数据集: 包含了14天内app推荐广告的记录,用户信息,广告信息以及安装的app的记录。论文使用了39个分类特征,去掉了最后2天噪声过大的数据,使用前11天数据作为训练,第12天的数据作为数据。最终22million训练集,2million测试集(11:1)
6.2 对比的方面
分别从AUC,cross entropy,pearson‘s R以及root mean squared error在线下,线上以及采用不同的operation来进行试验
6.2.1 Offline-training performance comparison
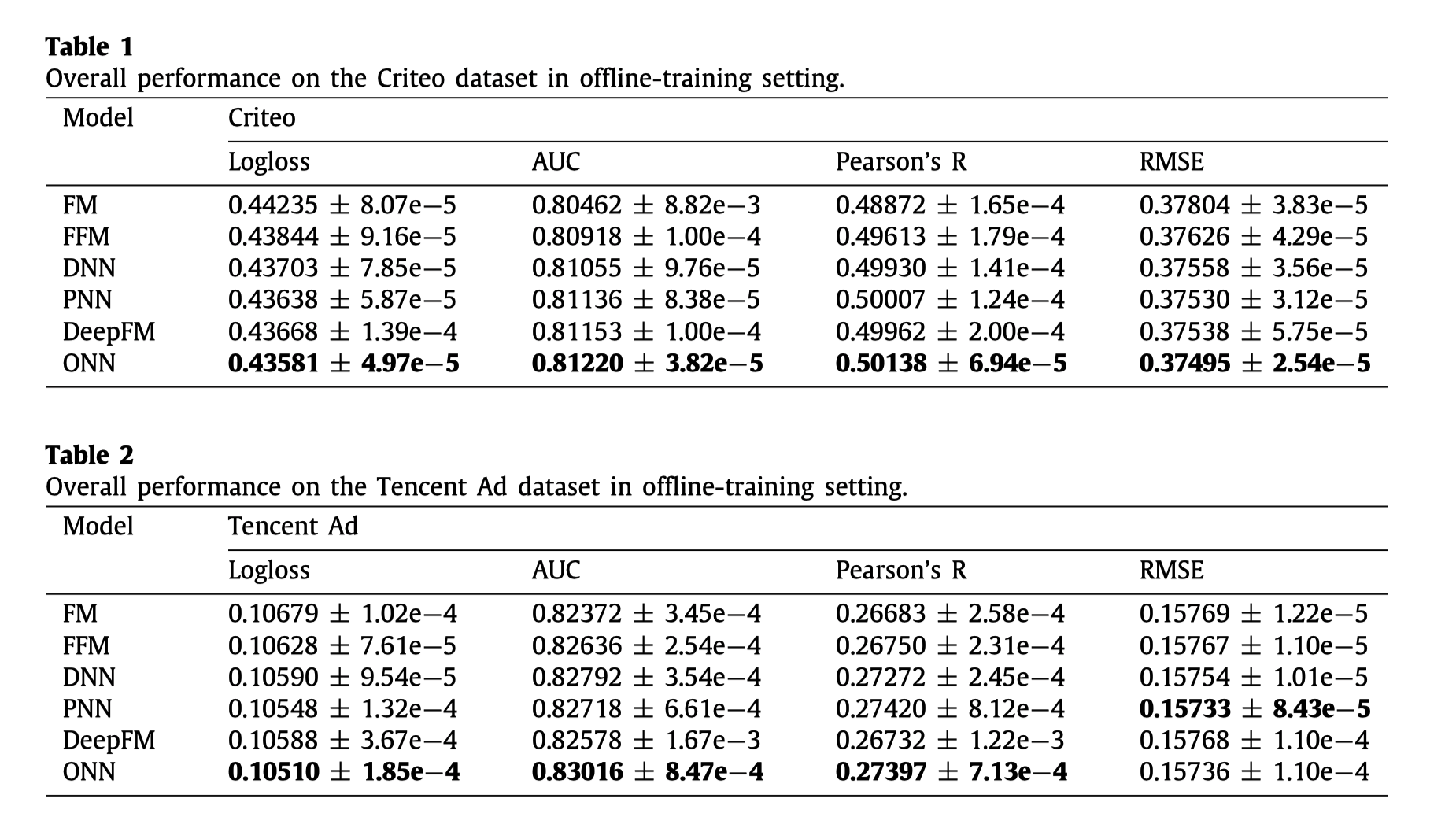
从上面这两张表格可以看出来的有:
- PNN这些加入了深度网络的模型效果要优于FM, FFM,说明了深层的模型效果是要优于浅层的网络
- FFM优于FM,ONN优于PNN,说明采用了operation aware embedding是优于一般的embedding层的
- PNN,DeepFM,ONN优于了DNN,说明了进行求积的操作是有效的。
6.2.2 Online-training performance comparison
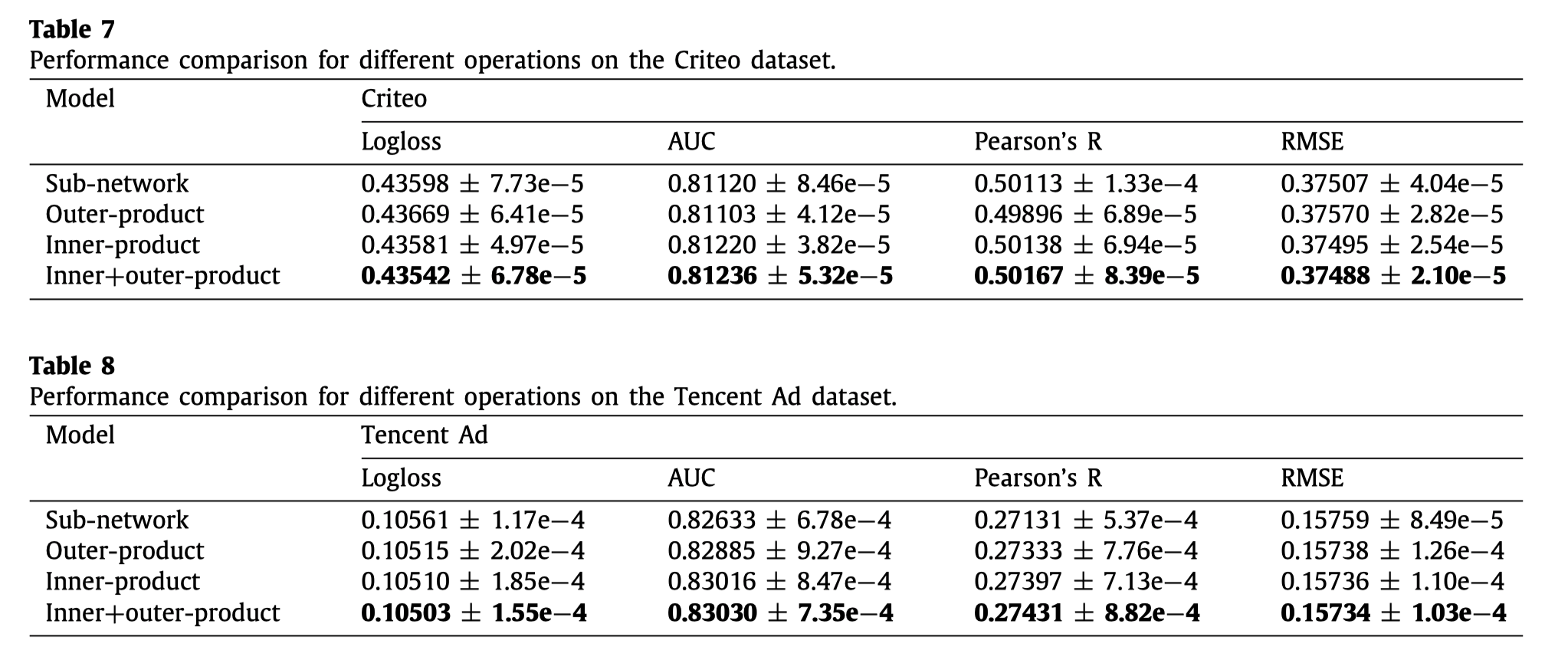
在线上的测试中,每一个测试样例只能够被训练一次,对于FM, PNN这些只有一种表示形式的模型来说,一次epoch就学到比较好的表示是比较难的。ONN依旧取得了最好的效果。
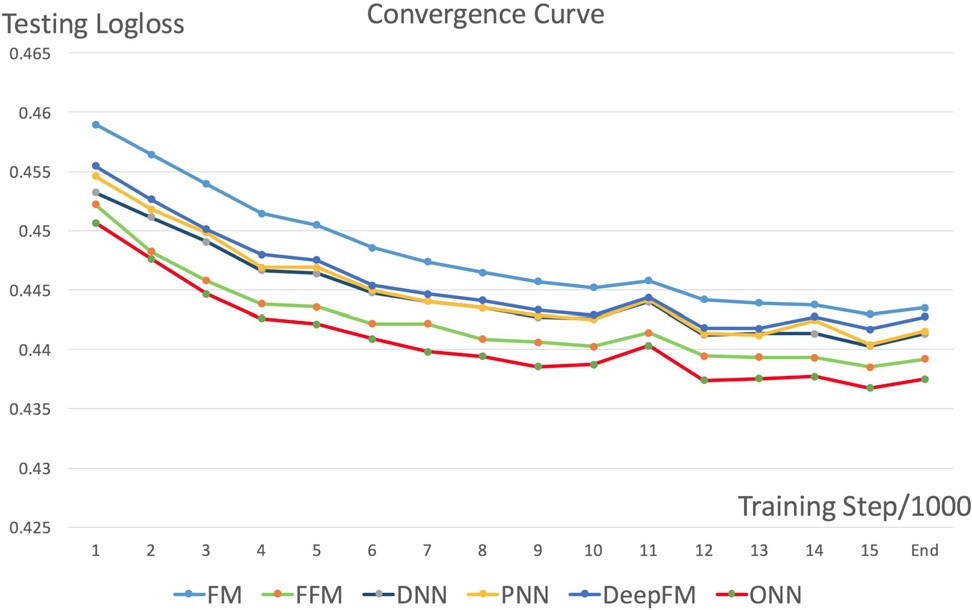
从上面的收敛趋势可以看到FFM,ONN这样使用了aware的模型,logloss收敛速度是由于其它模型的。
6.2.3 Analysis of different operations
默认情况下ONN是使用内积作为operation,论文中就inner-product, outer-product, sub-network, inner+outer-product四种operation进行了比较。
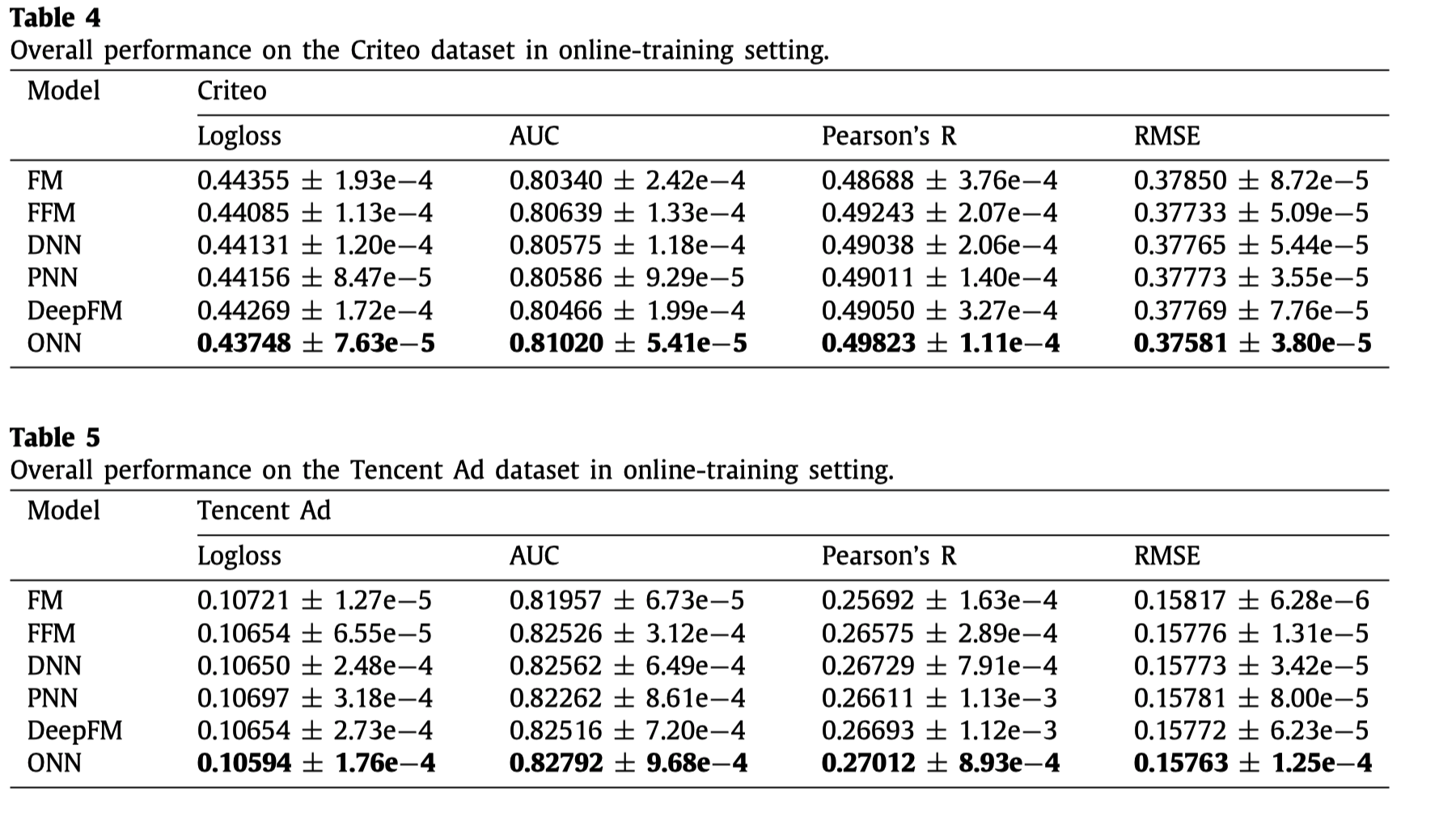
可以看到inner+outer-product获得了最好的结果,但是优势并不明显,考虑到时间和空间复杂性,它并不是一个很好的选择。所以依旧是使用了inner product。 但需要注意的是,sub-network取得的效果也是非常有竞争性的。而且它在Criteo数据集上的AUC指标上取得了很好的效果,这个可以考虑为下一步的研究方向。
7 总结
- 线上测试的结果表明ONN比较适合于线上的环境。
- operation aware这种想法可以考虑应用在其它地方