NGCF
Neural Graph Collaborative Filtering
论文的主要贡献是提出了一种embeding propagation的方式,能够利用high order范围内的实体,训练得到用户和物品的embeding。结合知识图谱做推荐。
1 介绍
协同过滤(CF)有两个关键的点:
一个是如何表示用户和物品(embeding),embeding的表示在各种方法里都不相同,可以直接使用用户/物品ID表示embeding,也可以利用各种特征,经过神经网络MLP,获得embeding表示。 另一个是如何表示两者的交互(interaction),在MF中,直接使用用户与物品vector的点积表示交互(即一个鼠标点击广告的动作,或者购买该物品的历史)。
但是多数模型都没有通过利用user-item的交互来训练得到embeding,只使用了用户属性等基本描述性的特征。
如果要利用交互来获得embeding,存在的问题在于若使用user-item矩阵的形式表示交互,这样矩阵规模就非常的大,常常达到几百万量级,而且非常稀疏。
为了解决这个问题,论文中将交互转换为graph的形式,集中注意力在有过交互的物品上,例子如下图:
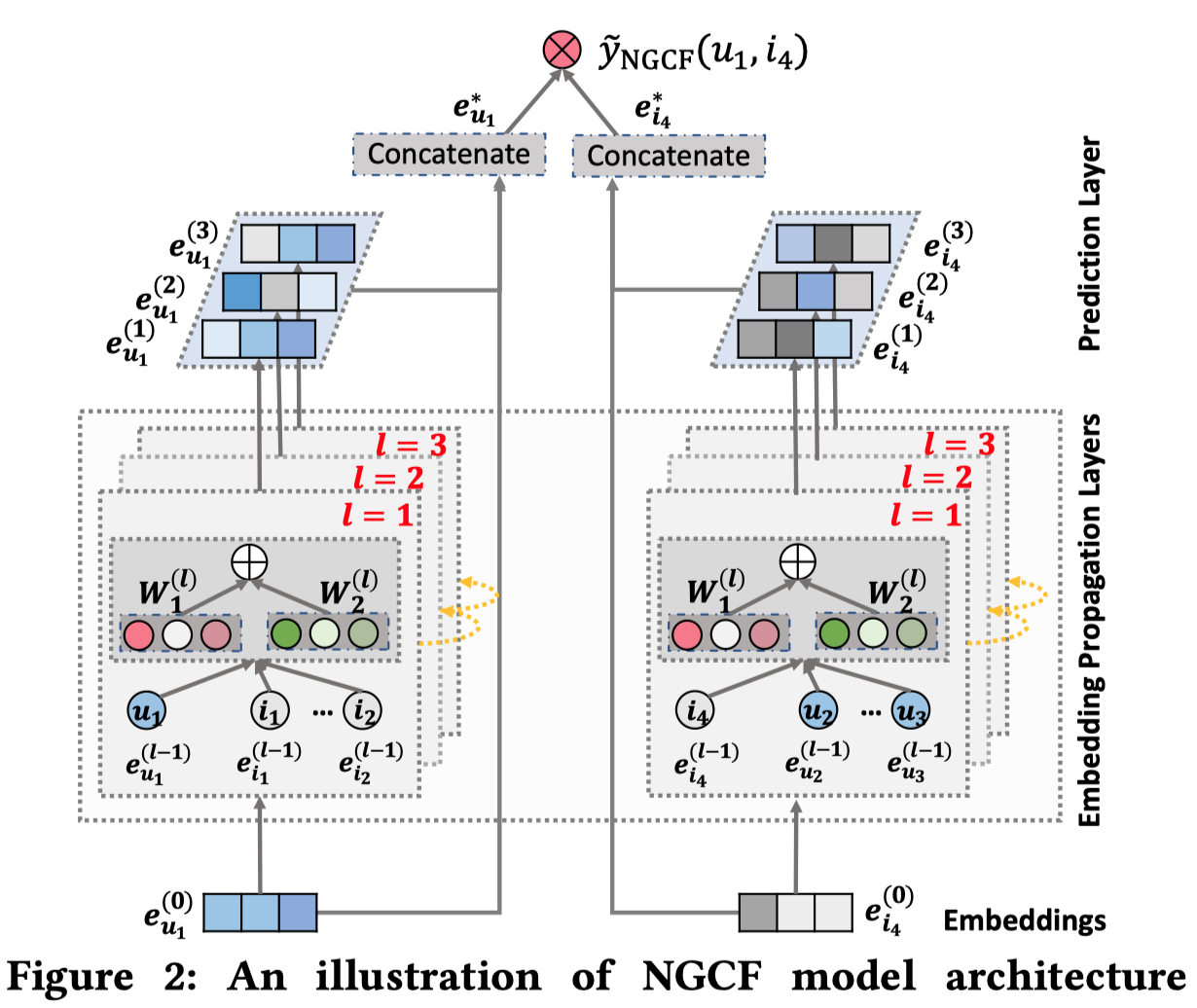
图中的用户u1是推荐的目标用户。右边的图看成是以\(u_1\)为根结点形成的一个树,这样对于\(u_1\)的预测,就由原来的\(i_1, i_2, i_3\)(first order)拓展到\(i_4, i_5\)(third order)这样的high order范围。
论文的主要贡献是提出了一种embeding propagation的方式,能够利用high order范围内的实体,训练得到用户和物品的embeding。
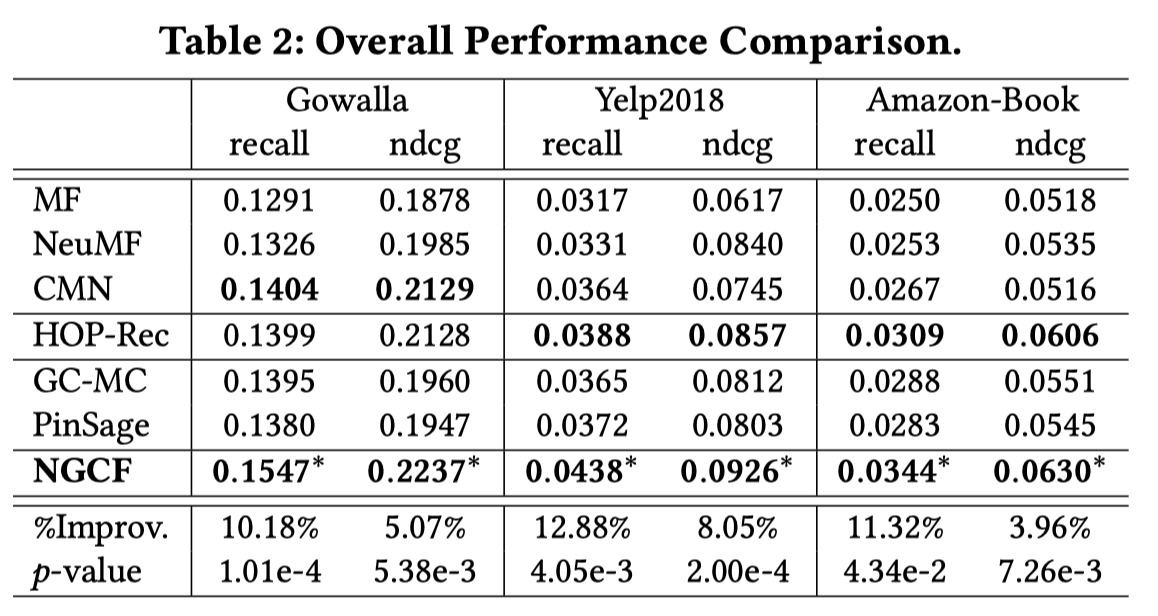
2 Model结构
NGCF一共包括三层,
- Embeding layer:表示user-item的look-up table
\[ E=[\underbrace{e_{u_1}, e_{u_2}, \dots}_{N\ users},\underbrace{e_{i_1}, e_{i_1}}_{M\ items} ]^T \]
- Embedding Propagation Layers: 利用embeding进行多层的propagation
- Prediction layer:预测\(<u, i>\)的概率
整个网络的结构如图:
2.1 Embedding layer
这一层与主流的推荐模型的embeding layer一样,对于N个用户u,M个物品i,使用d维的向量来表示,形成下面的矩阵(\((N+M)\times d\)): \[ E = [e_{u_1}, \dots, e_{u_N},e_{i_1}, \dots, e_{u_M},]^T, e_u, e_i\ \in R^d \] 在实现中首次训练使用xavier initializer初始化。
2.2 Embedding Propagation Layers
2.2.1 First-order Propagation
2.2.1.1 Message Construction
对于一个用户u,我们首先可以直接使用那些与用户有直接交互的物品计算用户的embeding,表示为 \[ m_{u\leftarrow i} = f(e_i, e_u, p_{ui}) \] \(m_{u\leftarrow i}\)称为物品i对于用户u的message embeding,\(f\)称为message encoding function,\(p_{ui}\)是系数,控制\(<u, i>\)这条path的权重。
具体的,\(m_{u\leftarrow i}\)表现为: \[ m_{u\leftarrow i} = \frac{1}{\sqrt{|N_{u}||N_{i}|}} \big( W_1 e_i + W_2 (e_i\odot e_u)\big),\ \ W_1, W_2 \in R^{d^{'}\times d} \] \(\odot\)表示element wise乘法,\(N_{u},\ N_{i}\)分别表示与用户u和物品i直接有交互的物品或者用户数量。
\(\frac{1}{\sqrt{|N_{u}||N_{i}|}}\)就是 \(p_{ui}\), 被称作graph Laplacian norm,它表示物品传递给用户的message的weight,可以这样理解,如果某个物品的\(N_i\)越小,表示这个物品越”独特“,越能够体现用户的个性偏好, \(p_{ui}\)增大;用户的\(N_u\)越小表示该用户的兴趣越”集中“,那么他的历史数据中的每个物品的 \(p_{ui}\)都应该增大,表示每个物品都能够较大的反映该用户偏好。
2.2.1.2 Message Aggregation
对于一个用户u的多个物品i,得到了多个传递过来的message embeding,需要使用一种聚合起来形成最终的用户embeding的方式, \[ e_u^{(1)} = LeakRelu\big( m_{u\leftarrow u} + \sum_{i \in N_u} m_{u\leftarrow i} \big),\\ m_{u\leftarrow u}=W_1 e_u \] \(e_u^{(1)}\)是用户u经过第一次embeding propagation之后的embeding,可以看到最终聚合的方式是直接对所有的message embeding相加,最后联合原来的表示\(e_u\),经过一个leak-relu就得到了最后的表示。
上面过程以单个用户u为例,介绍了一次embeding propagation的过程。这个过程对于物品i也是一样的。
单个用户进行一次propagation,与用户u直接相连的所有物品的”信息“传递到了用户u上。但这个过程是同时在所有的用户u和物品i都进行的。一次propagation,让每个用户和物品都得到了从与它们直接相连的实体的信息。如果在进行一次propagation,用户和物品目前包含了自己下层直连的信息,就又会传递给上级。也就实现了获取high order连接信息的目的。
2.2.2 High-order Propagation
在first order propagation的基础上,得到多次propagation的表示, \[ \begin{cases} e_u^{(l)} = LeakRelu\big( m_{u\leftarrow u}^{l} + \sum_{i \in N_u} m_{u\leftarrow i}^{l} \big),\\ m_{u\leftarrow u}^{l}=W_1^{l} e_u^{(l-1)},\\ m_{u\leftarrow i}^{l} = \frac{1}{\sqrt{|N_{u}||N_{i}|}} \big( W_1^{l} e_i^{(l-1)} + W_2^{l} (e_i^{(l-1)} \odot e_u^{(l-1)})^{(l-1)} \big) \end{cases} \]
2.2.3 Propagation Rule in Matrix Form
之前的例子作用于所有的用户和物品,就得到了矩阵形式的表达, \[ E^{(l)} = LeakRelu \big( (L+I)E^{(l-1)} W_1^{l} + LE^{(l-1)} \odot E^{(l-1)} W_2^{l}\big) \] 其中\(L \in R^{(N+M)\times(N+M)}\),\(L_{ui}=\frac{1}{\sqrt{|N_{u}||N_{i}|}}\)。
2.3 Model Prediction
经过l次propagation,一个用户u,得到\(\{e_u^{1}, \dots ,e_u^{l}\}\),在本论文里,直接将l个d维的embeding concat到一起。 \[ e^*_u =e_u^{0}|| \dots ||e_u^{l},\qquad e^*_i =e_i^{0}|| \dots ||e_i^{l} \] 那么最后对于用户u,物品i的得分通过求内积得到, \[ \hat{y}_{NGCF}(u,i) = (e^*_u)^T e^*_i \]
2.4 Optimization
损失函数为BPR(Bayesian Personalized Ranking) loss, \[ Loss = \sum_{(u, i, j)\in O}-ln\sigma(\hat{y}_{ui}-\hat{y}_{uj}) + \lambda {\lVert \theta \rVert}_2^2 \\ O = \{ (u, i, j)|(u, i)\in R^+,\ (u, j)\in R^- \} \] 使用Adam,early stoping。
为了防止过拟合,类似dropout方法,使用了两种dropout:
- Message dropout:以一定的概率\(p_1^{l}\),在进行第l次embeding propagation时,丢弃一些用户或物品message embeding 。message dropou作用于\(E^{(l)}\)。
- Node dropout:以一定的概率\(p_2^{l}\),在进行第l次embeding propagation之前,丢弃上次产生的一些用户或物品的embeding 。实际是都使用了0.1概率。node dropout作用于\(L\).
3 Eexperiments
在3个数据集上讨论了3个问题:
- 本文提出的NGCF和其它CF模型的比较
- NGCF不同超参数的影响
- 能够利用high order connectivity信息,对于用户和物品的表示的影响
3.1 Dataset
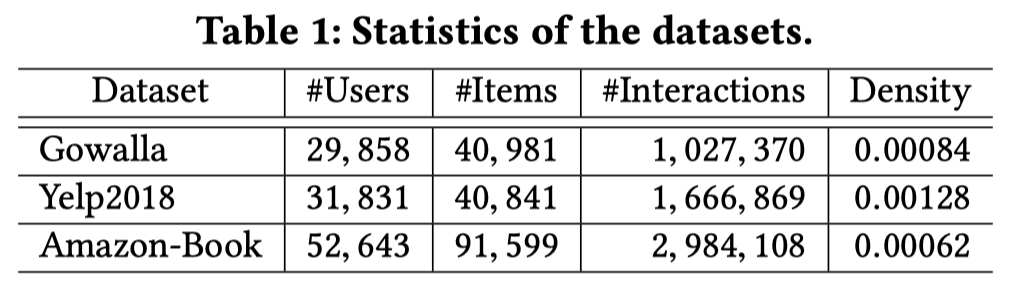
使用10-core形式,每个用户至少有10个历史交互数据。
80%的interaction为训练集,20%为测试集。
3.2 Experimental Settings
评估指标针对每个用户推荐K个物品,然后计算 \(recall@K,\ ndcg@K\),默认情况下K设置为了20。
一些实验的超参数如下:
- batch size:1024
- embeding size:64
- ndcf layer:3,[64, 64, 64]
- dropout: 0.1
- message out: 0.1
3.3 RQ1: comparison
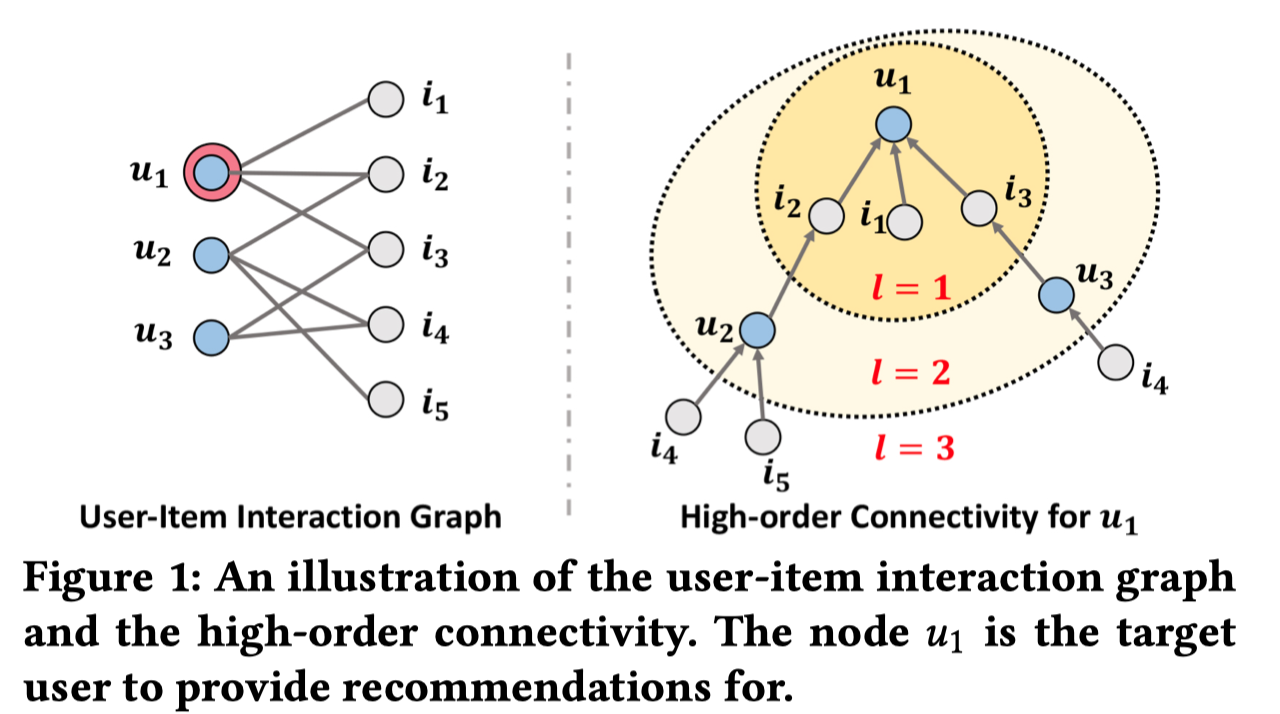
3.3.1 Overall Comparison
对比了几个不同的CF算法如下
3.3.2 Comparison w.r.t. Interaction Sparsity Levels.
一个用户的推荐效果和这个用户的历史数据数量有很大的关系,如果交互的数量越少,越难推荐合适的物品,针对不同交互量用户分组进行了下图的研究。
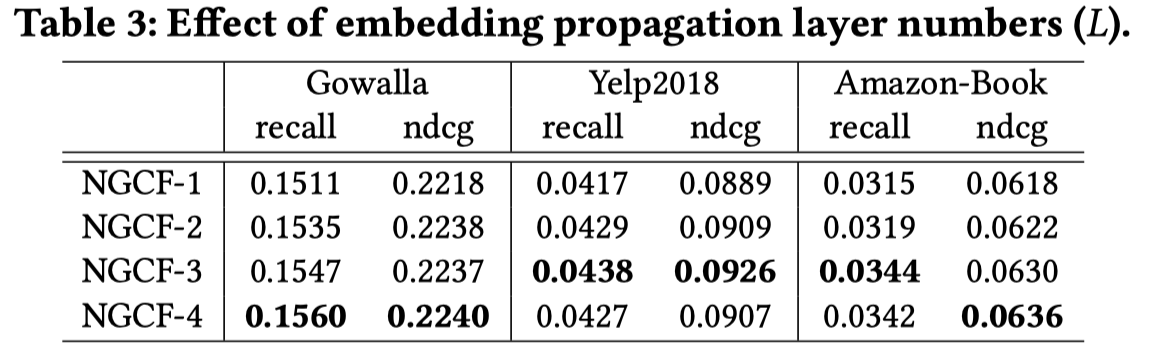
图上能够看到在不同的分组下,NGCF都有最好的ndcg@20结果。
3.4 RQ1: Study of NGCF
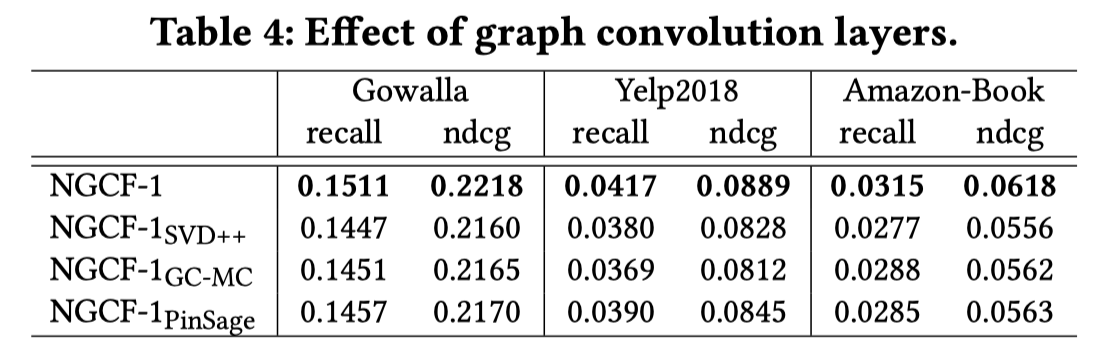
3.4.1 Effect of Layer Numbers
针对NGCF不同层数产生的效果的研究,NGCF-4虽然在两个数据集上得到了较好的结果,但是提升并不大,而且参数数量增多,训练成本增加,也容易过拟合。
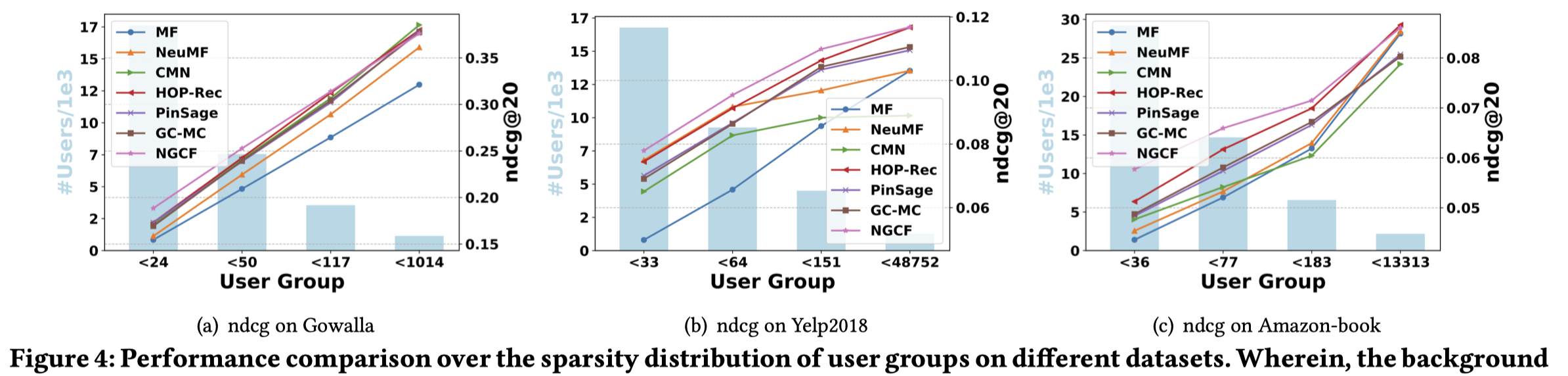
3.4.2 Effect of Embedding Propagation Layer and LayerAggregation Mechanism
对于embeding propagation的方式,进行了研究,
3.4.3 Effect of Dropout
研究在不同数据集下,node和message dropout不同数值对于结果的影响
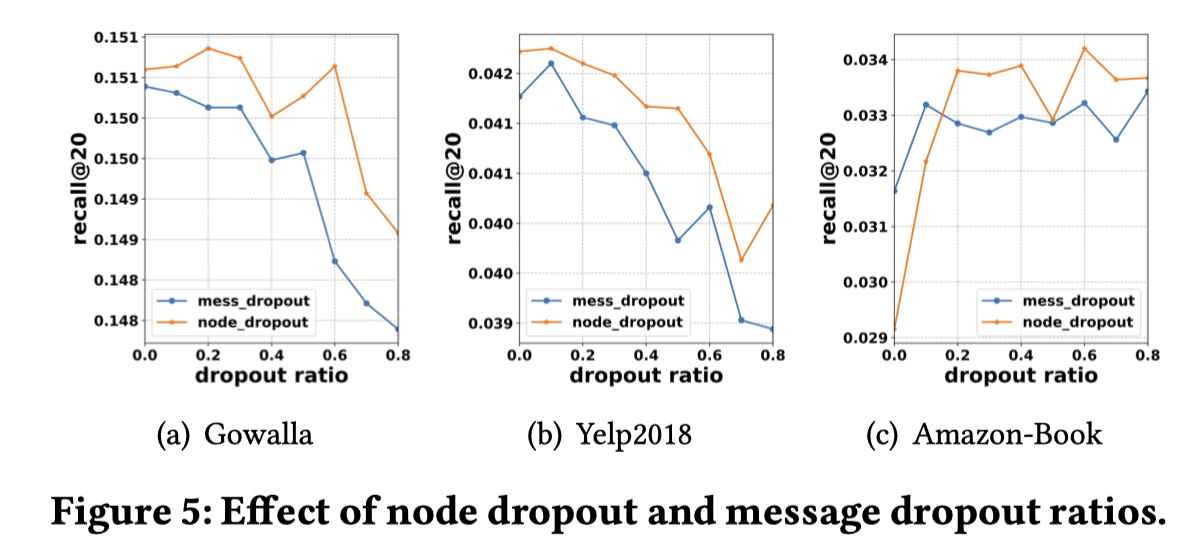
结果显示多数情况下,相同概率的node dropout方式好于message dropout,而且node dropout方式得到的最好效果要优于message dropout。
一个可能的原因是node dropout会直接丢弃原来的node,这些node不会产生任何的效果,具有更强的鲁棒性。
3.5 RQ3: Effect of High-order Connectivity
为了研究利用high-order connectivity是否有效果,在Gowalla测试数据集中,截取6个用户和它们的物品在NGCF-1和NGCF-3下的embeding,利用t-SNE进行探究。
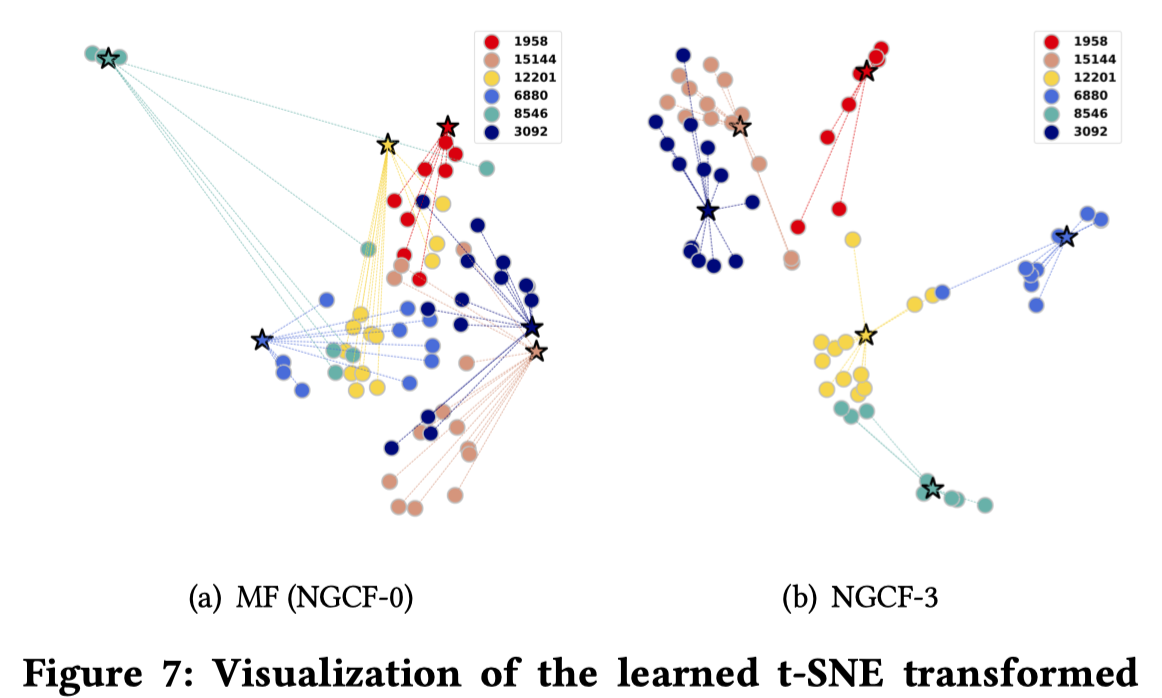
从图上可以看出来,在3-order下,一个用户和它的物品更加倾向形成一聚类,即通过它的物品,能够更好的反映用户的实际情况。这表示利用high-order起到了作用,能够更好的捕获协同信息。
4 Conclusion
论文的主要成果
- 一种新的embeding propagation方式
- 在三个数据集上进行的不同的研究
下一步方向
- 现在每层的neighbor的权重都是一样的,可以考虑加入attention(在作者的下一篇论文KGAT中实现了)
- 结合知识图谱(KGAT)
- 结合social network,cross-feature等
不足
- 单纯的使用了用户的历史交互信息,用户和物品的其它特征并没有利用,能否结合FM, NFM,得到更加丰富的embeding?