entropy-softmax

发表于 更新于 分类于 ， 阅读次数： 本文字数： 4.3k 阅读时长 ≈ 4 分钟

机器学习中的Sigmoid、Softmax与entropy

这篇文章期望总结与讨论机器学习中常见的sigmoid、softmax函数与entropy熵。

参考资料：

  1. 熵，维基百科
  2. sigmoid函数推导，知乎
  3. 一文详解Softmax函数，知乎
  4. S型函数，维基百科
  5. 信息熵越大，信息量到底是越大还是越小？，知乎
  6. softmax和cross-entropy是什么关系？

总结：

  1. sigmoid可以看做是神经网络输出\([p,0]\)的softmax变形\([e^x/(e^x+1), 1/(e^x+e^0)]\)，只不过由于对应标签1的概率\(p\)是我们的期望值，另外一个0不做过多讨论。
  2. softmax+交叉熵基本是绑定的，这是因为会使得loss的计算和求导都更简单。
  3. 我们经常使用交叉熵，是因为它作为KL散度的核心变化部分，能够衡量输出分布和真实分布之间的差异。
  4. 使用softmax而不是hardmax的目的是期望能够让模型从不同类的预测值上获得更多的梯度。

Sigmoid函数

在机器学习领域，如果在了解完线性回归（linear regression）后，发现线性回归很难拟合非线性的分布；那么你很快能看到一个强大的分类器，逻辑斯蒂回归。

逻辑斯蒂回归，logistics regression，就是在线性回归的输出加上了一个特殊的非线性函数，sigmoid函数（在很多文章，也把sigmoid函数叫做S型函数，而把逻辑斯蒂回归中使用的非线性函数单独称作logistic function）：

\[ f(x)=\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+1} \]

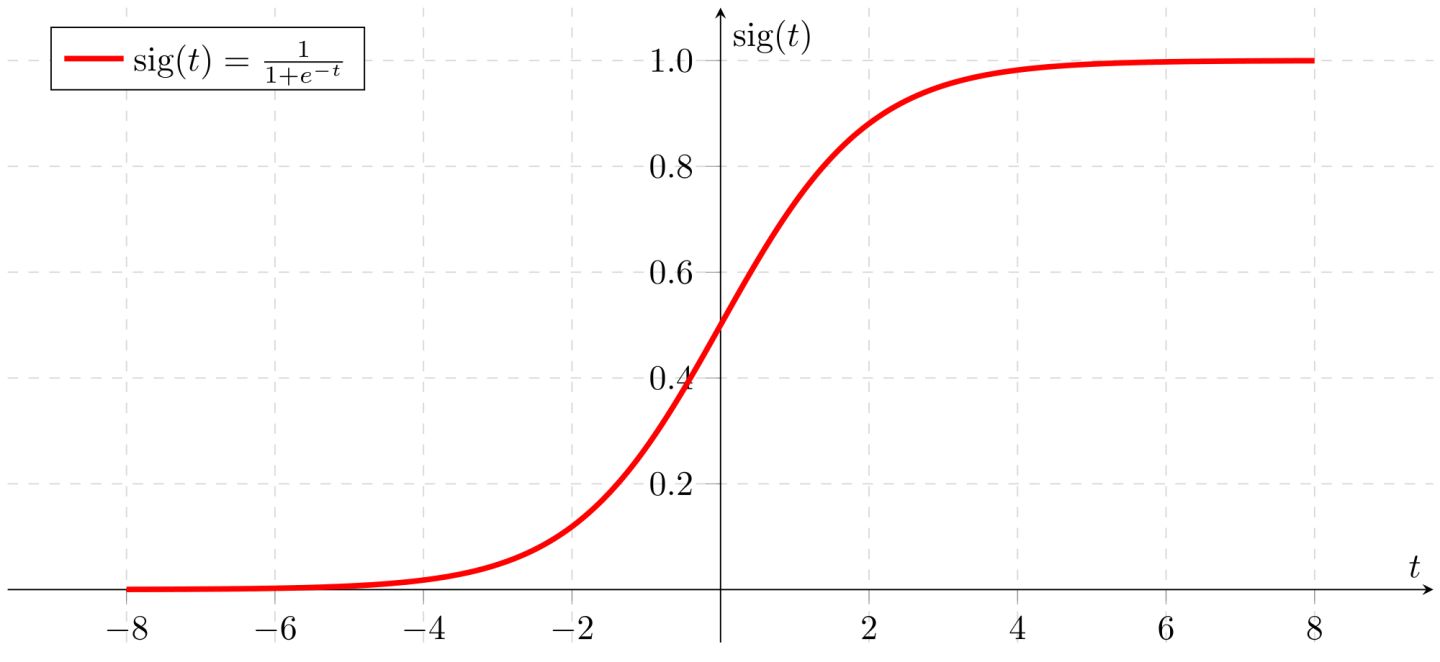
该函数是S型函数的一种，指其函数形状类似于S。S型函数在实数范围内可微，并且只有一个拐点（指函数凹凸发生变化的点）。S型函数还包括了很多其它的函数形式。

sigmoid函数取值在\([0,1]\)，常被用来输出单类预测区间在\([0,1]\)的任务。sigmoid函数的导数是以他自身为因变量的函数，\(f^\prime(x)=F(f(x))\)：

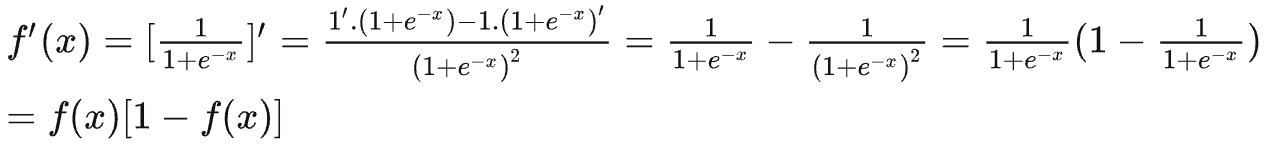
Softmax函数

如果我们期望进行单标签多类预测，比如某篇文章/某张图片属于什么主题，最后输出的一个序列\([0,0,1,0,0,\dots]\)。注意这种情况下，所有类的和是1，仍然是单标签预测。如果是多标签预测，那么会出现多个同时成立的\(1\)。

在这种情景中，在模型不变的情况下，试想下我们还可以使用sigmoid函数来预测吗？

模型此时的输出\(\bf{x}\)是一个实数向量\([0.23472,11.78,-99.99,0.0,\dots]\)，我们可以对每个element分别应用sigmoid函数，那么它可以转化成期望的01预测序列。

但这样做有什么问题？

每个element是独立判别的，比如每个主题都会得到自己的\(0-1\)估计，它们的和不能保证是\(1\)。这种做法适用于多标签的情况，但不适用于单标签多分类。单标签多分类的概率和应该是1，并且从直觉角度看，不同类之间应该存在信息的互相影响。

为了解决上述问题，softmax是对于sigmoid函数的拓展： \[ softmax(x_i)=\frac{e^{x_i}}{\sum_{j=1}e^{x_j}} \] 上述形式和sigmoid进行对比后可以发现，sigmoid函数的分母部分是两个元素和，除了\(e^x\)之外多了\(1\)。而softmax函数是所有预测元素/概率的\(e\)指数和作为总的分母。

从值的角度来看，softmax通过平均，保证了输出值在\([0,1]\)。

为什么叫做soft的max？

想一下，我们完全可以直接把最大的那个实数拿出来作为预测结果（这就叫做hard max）。我们为什么非要求和以后，再计算最大实数在和中的占比呢？

因为在很多情况下，我们并不想直接丢掉其它类的预测值，我们往往希望能够获得神经网络对所有类的预测概率。

从优化的角度讲，直接把最大的实数挑出来，那么就只会依据这个实数对应的类进行优化，比如它对应的类不是真实标签，那么优化器会强迫神经网络在接下来对这个类的预测值减小，但是不会同时强迫神经网络对其它标签（包括真实标签）的预测值增大/减小。如果它对应的类是真实标签的话，那么优化器会会强迫神经网络在接下来对这个类的预测值增大，但是不会同时强迫神经网络对其它标签的预测值更小。这种做法不是一种很理想的决策。

另外，softmax对于目标标签的概率输出考虑到了其它类（作为分母）。这样在优化的时候，其它类对应的神经元也能够得到对应的梯度。相反，直接hardmax把最大的挑出来，那就只有最大值对应的神经元可以得到优化了。

接下来讨论为什么引入指数底\(e\)？而不是直接求和？下面解答来自一文详解Softmax函数，知乎。

\(e^x\)的斜率逐渐增加，随着\(x\)越来越大，斜率也越来越大。这就导致了，引入\(e^x\)会拉大不同预测概率之间的差距，这实际相当于增加了马太效应，即强者越强，一个输出值\(z_i\)增加很小的幅度，也会被\(e^x\)放大。

1
2
3
4
5
6
7
8
9
10
import tensorflow as tf

print(tf.__version__) # 2.0.0
a = tf.constant([2, 3, 5], dtype = tf.float32)

b1 = a / tf.reduce_sum(a) # 不使用指数
print(b1) # tf.Tensor([0.2 0.3 0.5], shape=(3,), dtype=float32)

b2 = tf.nn.softmax(a) # 使用指数的Softmax
print(b2) # tf.Tensor([0.04201007 0.11419519 0.8437947 ], shape=(3,), dtype=float32)

同时，\((e^x)^\prime=e^x\)，求导比较方便。

引入指数就没有缺点吗？

当然有，指数函数在\(x\)比较大时，会输出过于大的值：

1
2
3
4
5
import numpy as np

scores = np.array([123, 456, 789])
softmax = np.exp(scores) / np.sum(np.exp(scores))
print(softmax) # [ 0.  0. nan]

在深度学习框架TensorFlow中，因为softmax和交叉熵通常是一起的，因此设置了额外的loss函数同时实现了softmax和交叉熵的计算，避免出现上述情况。

接下来我们要讨论softmax函数的求导。

\(p_i=softmax(x_i)\)函数，分母包括了所有的\(x_j\)，而分子只包括\(x_i\)。所以我们要分类讨论。

当\(j==i\)时，对\(x_j\)也就是\(x_i\)进行求导，此时分子要参与求导（下面的\(z\)就是前面的\(x\)）：

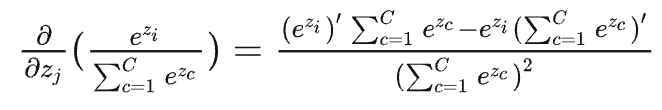
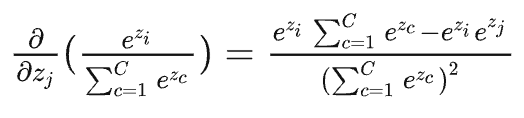
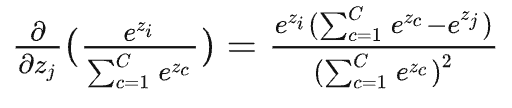
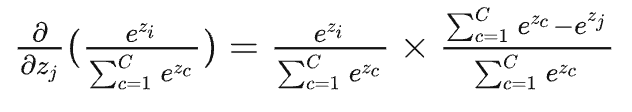
上述公式可以写成，\(p_i\times (1-p_j)\)，由于\(i==j\)，因此最终结果为\(p_i-p_i^2\)。

当\(j\ne i\)时，对\(x_j\)进行求导，分子导数是\(0\)：

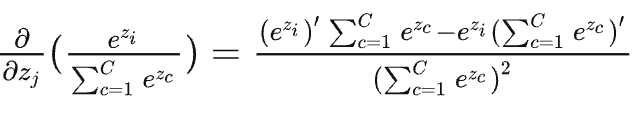
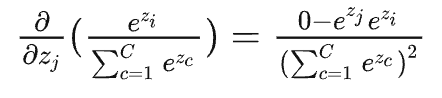
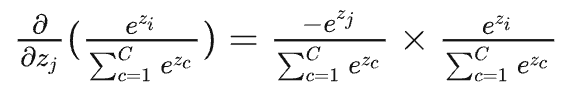
最终结果为，\(-p_j\times p_i\)。

即，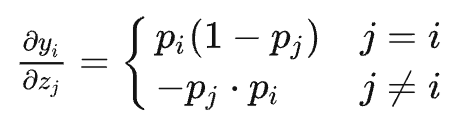

softmax的导数形式意外的简单，可以直接利用前馈过程中计算出的结果算出导数。

在使用了softmax之后，我们得到了预测序列\([0.11,0.43,0.006,\dots]\)，那么怎么样计算loss呢？

我们首先可以给softmax输出结果加上一个\(log\)，这样不改变它的单调性：

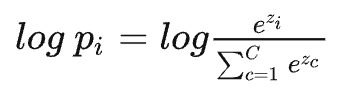
那么接下来假设\(i\)的真实标签就是\(1\)，如果我们让\(log(p_i)\)不断增大不就可以了吗？当然，loss一般是越小越好，所以有：

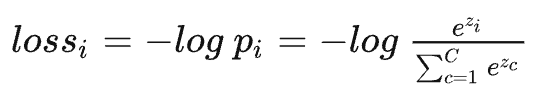
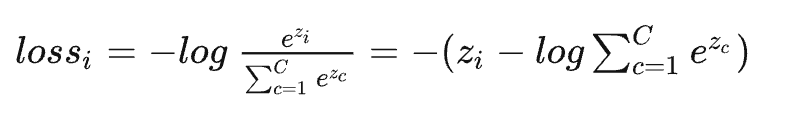
记住上面的式子，在推导交叉熵的时候，两者会统一起来。

Entropy熵

信息论中的熵的概念，由1948年，克劳德·艾尔伍德·香农將熱力學的熵引入，因此也叫做香农熵。熵是对不确定性的度量，不确定性越大，熵越大。

熵的数学定义为： \[ H(X)=E[I(X)]=E[-ln(P(X))]=E[ln(\frac{1}{P(X)})] \] 即随机事件/变量，概率的平均期望。

对于有限样本：

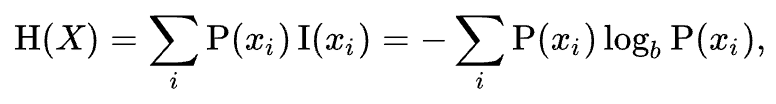
在这里\(b\)是对数所使用的底，通常是2,自然常数e，或是10。当\(b = 2\)，熵的单位是bit；当\(b = e\)，熵的单位是nat；而当\(b\) = 10,熵的单位是Hart。

投一次硬币，出现的花纹（正反面）这个事件的不确定性是1 bit。

熵和信息量有什么区别？

不能简单的把熵就认为是信息量。事实上熵减才能衡量信息量的增加。我们往一个事件/随机变量当中注入新的信息，比如额外事件的发生，不确定性才会减小。

在信息世界，熵越高，则能传输越多的信息，熵越低，则意味着传输的信息越少。这句话表达的是随机变量能够容纳/表达的信息量的大小和熵是有关的。

香农对于某个确定的事件发生后的信息量的定义，核心是发生概率越小，一旦发生后，信息量越大： \[ h(x)=-log_2(p(x)) \] 然后介绍下交叉熵，用来衡量两个独立变量的分布差异：

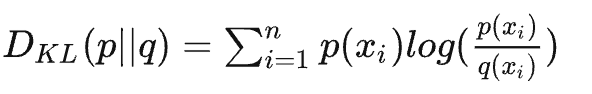
评估变量Q和变量P分布差异的大小，如果两者分布完全一致，KL散度值为0；KL散度值越大，分布差异越大；KL散度值越小，分布差异越小。

在机器学习中，如果我们把P看做是真实分布，Q是模型预测的分布，那么KL散度可以衡量机器学习模型的预测性能。在这种情况下，对KL散度进一步推导：

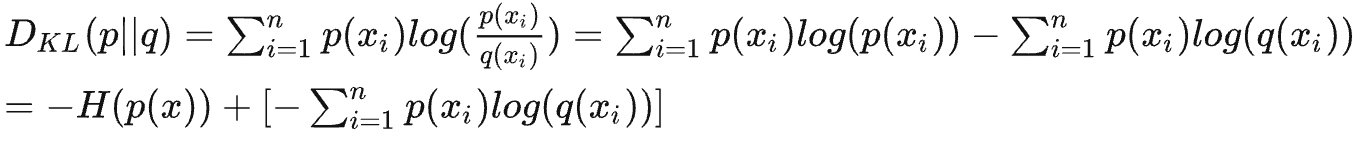
公式的前半部分是真实分布P的负熵，后半部分就是真实分布P做系数、log预测分布Q的交叉熵（同时包括了真实和预测分布，所以叫做交叉）。

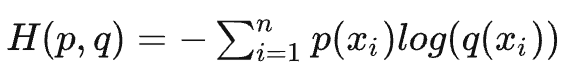
前半部分是个固定常量，只要后半部分越小，KL散度就越小。

在了解到什么是交叉熵之后，我们再回到使用softmax推导出的式子：

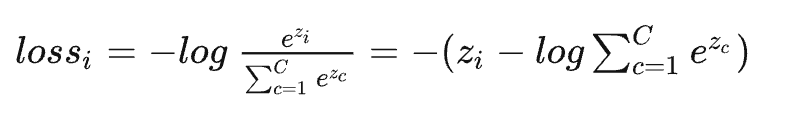
对于常常使用one-hot编码标签值的机器学习算法来说，只有正确类标签值是1，其它是0：

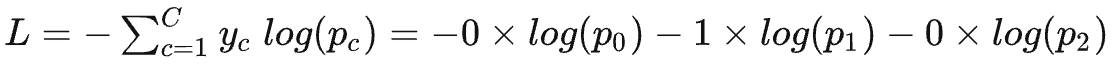
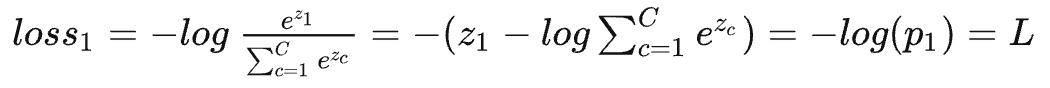
也就是两者完全等价。

然后使用交叉熵进行求导：

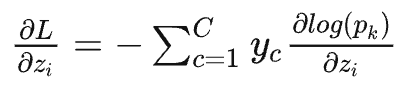
最后的求导结果，只需要预测值和实际标签就能得到导数。

这就是当拿交叉熵和softmax一起做loss时候的优点，求导更加简单。

另外一点是，当计算出softmax之后，再计算交叉熵： \[ S= \sum_j y_k\times log(S_j) \] 如果\(S_j\)是softmax输出结果，那么，可以一步到位直接计算logSoftmax：

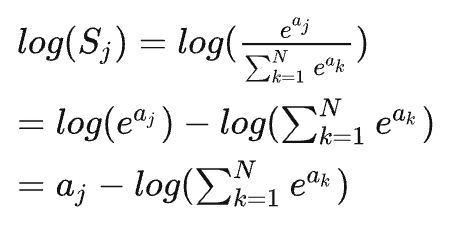
在pytorch的nn.CrossEntropyLoss()函数实现中，就是直接输入神经网络计算得到的激活值\(a_j\)（无需经过Softmax）即可，nn.CrossEntropyLoss()会按照logSoftmax来计算最终的loss