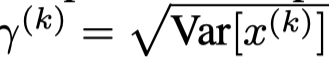Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
ICML 2015
谷歌团队的经典论文,batchnorm操作。题目中的Internal Covariate Shift是论文中提出的一个名词,主要是指在网络结构中,由于各层模型参数不同,每一层接受的输入的分布都会改变。这种现象被称作internal covariate shift。这篇文章通过对把每层的激活值做归一化处理,提升模型训练速度与效果。
归一化处理会增大feature之间的相对差异,排除绝对差异,因此可能更好训练。另外,归一化操作能够让激活值处于激活函数类似sigmoid的梯度较大的区域,能够缓解梯度消失问题。
pytorch中的核心公式:

\(\gamma\)和\(\beta\)是两个很重要的可学习的参数,它从理论上保证归一化后的值\(y\)通过学习合适的\(\gamma\)和\(\beta\)可以还原原来的\(x\)。比如:
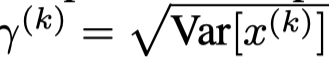

在mini-batch训练策略下的核心算法,对第\(i\)维的激活值\(x\)。

从博客上找的python代码实现方便理解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| def Batchnorm_simple_for_train(x, gamma, beta, bn_param):
"""
param:x : 输入数据,设shape(B,L)
param:gama : 缩放因子 γ
param:beta : 平移因子 β
param:bn_param : batchnorm所需要的一些参数
eps : 接近0的数,防止分母出现0
momentum : 动量参数,一般为0.9, 0.99, 0.999
running_mean :滑动平均的方式计算新的均值,训练时计算,为测试数据做准备
running_var : 滑动平均的方式计算新的方差,训练时计算,为测试数据做准备
"""
running_mean = bn_param['running_mean']
running_var = bn_param['running_var']
results = 0.
x_mean=x.mean(axis=0)
x_var=x.var(axis=0)
x_normalized=(x-x_mean)/np.sqrt(x_var+eps)
results = gamma * x_normalized + beta
running_mean = momentum * running_mean + (1 - momentum) * x_mean
running_var = momentum * running_var + (1 - momentum) * x_var
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return results , bn_param
|
论文实际没有完整读一遍,只看了核心算法方便实验,以后找时间从头看一遍。