Fast-weights-RNN

Using Fast Weights to Attend to the Recent Past

NIPS 2016

作者将fast weights引入到RNN中实现了更好的效果。本质上是在RNN的t时刻到t+1时刻中间，插入了一段新的RNN结构，每个step计算之前的隐藏状态和当前隐藏状态的关系权重，不断累加，最后达到比较好的效果。

这里需要先介绍下fast weights。

在1987年的时候，有一篇paper《Using Fast Weights to Deblur Old Memories》，提出了下面的说法：

Despite the emerging biological evidence that changes in synaptic efficacy at a single synapse occur at many different time-scales (Kupferman, 1979; Hartzell, 1981), there have been relatively few attempts to investigate the computational advantages of giving each connection several different weights that change at different speeds.

意思是说如果把一个weight的更新看做是神经元的一次神经活动，那么weight的更新也应该是有不同time scalse的。

那么如果模仿这个过程，除了一般的weight外，还可以尝试加入其它time scale的weight，也就是fast weight，fast weight用来模拟短时的记忆。

• Slow weight: The slow weights are like the weights normally used in connectionist networks-they change slowly and they hold all the long-term knowledge of the network.
• Fast weight: The fast weights change more rapidly and they continually regress towards zero so that their magnitude is determined solely by their recent past.

来看一下作者具体怎么样把fast weight引入到RNN中：

首先定义一个fast weight matrix：

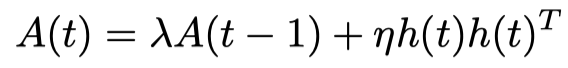
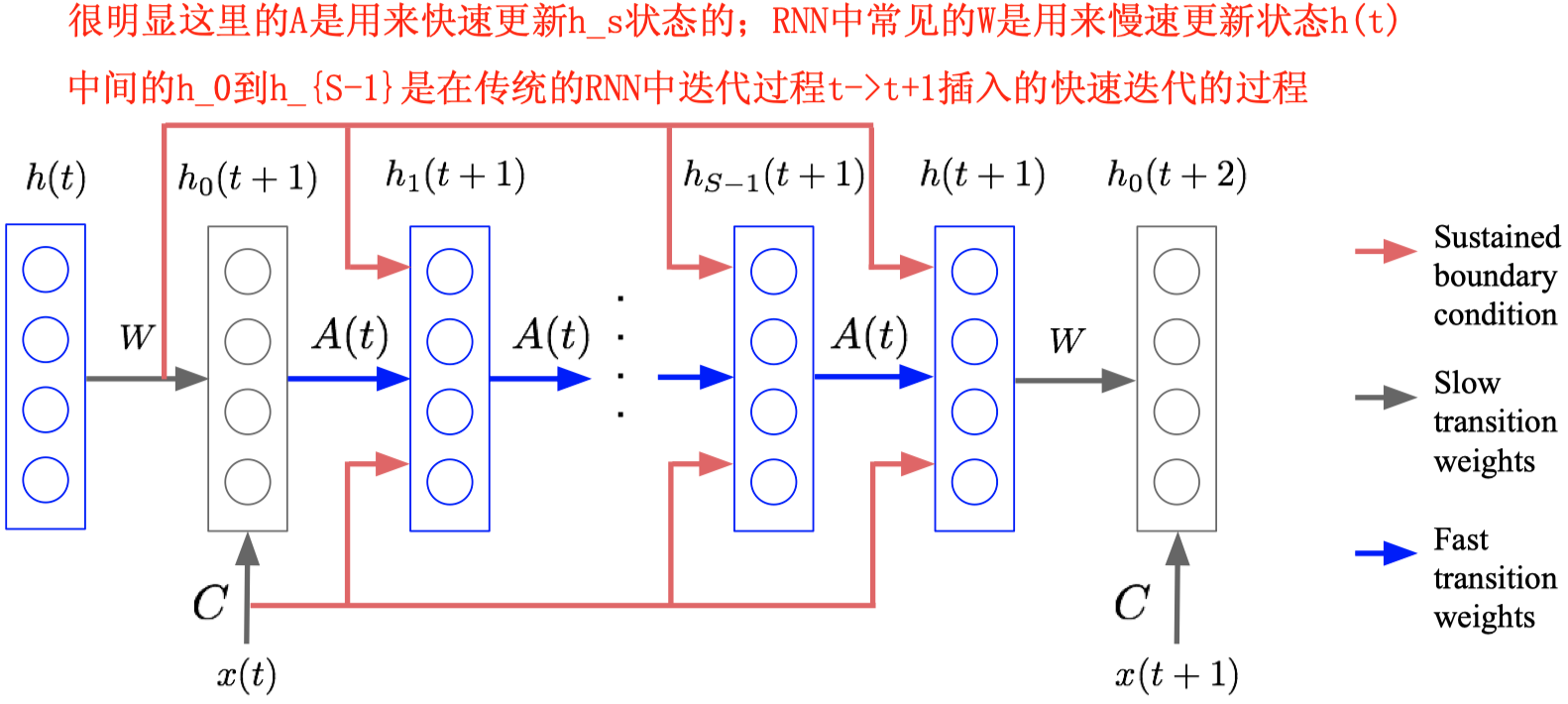
然后在RNN的\(t\) step到\(t+1\) step中间，插入新的多个step：

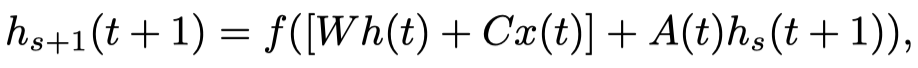
从这里可以看出来，\(A\)被用来快速更新状态。

由于实际中，sequence的time step数量是要比定义的hidden state vector的维度要小的，所以最后计算出来的A实际上远远不是一个满秩的矩阵。为了计算方便，作者假定对于不同sequence，\(A\)的初始值是0，那么有：

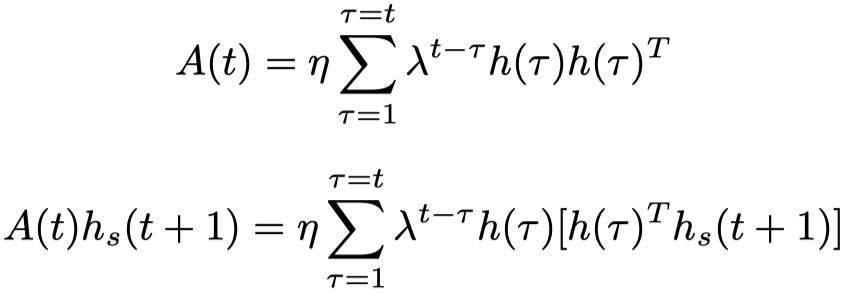
通过简单计算之前时刻隐藏状态和最近隐藏状态的点积，作为权重（也是attention），然后加上以前的隐藏状态，计算很快速。

作者还使用了layer normalization来防止两个向量的点积可能出现的数值消失或者爆炸的问题。