Essence-of-linear-algebra-3b1b
Essence of linear algebra
这篇文章是3blue1brown的Essence of linear algebra系列视频的笔记
- Vectors
- Linear combinations, span and basis vectors
- Linear transformations and matrices
- Matrix multiplication
- The Determinant
- Inverse Matrices, column space and null space
- Nonsquare matrices as transformation between dimensions
- Dot products and Duality
- Cross products
- Change of basis
- Eignvectors and eigenvalues
- Abstract vector spaces
1 Vectors
如何认识向量?
从一个物理学生的角度来看,一个向量是长度一定,角度一定,在空间中可以任意的移动。
从一个计算机学生的角度来看,一个向量是一系列数字的list,这些数字可能具有独特的现实含义,比如房子的面积、单位售价等。
从一个数学学家的角度来看,向量可以代表任何事物,只要能够保证向量相加和向量数乘有意义即可。
如果尝试从几何的角度来看,可以看做坐标系下的箭头,起始点是原点,向量是坐标系下的不同数轴的坐标,这些坐标说明了如何从原点到达箭头的终点。
向量的加法,可以看做是先沿着向量\(x\)运动,然后沿着向量\(y\)运动。
向量的数乘,就是长度的缩放操作。
2 Linear combinations, span and basis vectors
向量可以看做是基向量的线性组合,不同坐标,表示缩放不同数轴上的基向量。
span的定义:
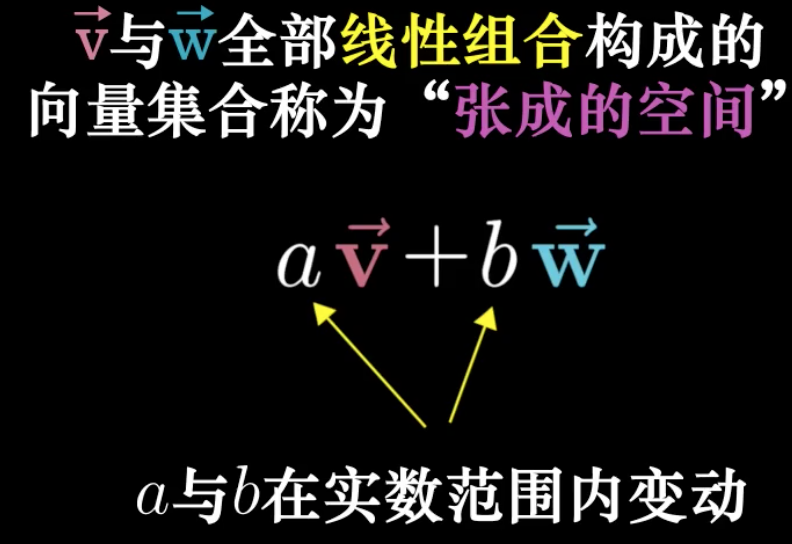
basis vector的定义:

3 Linear transformations and matrices
Linear transformation:
- transformation就是一种函数,用在线代领域是为了强调对于向量的变换操作
- 前面的linear有两个限制:转换后的直线仍然是直线,并且原点保持固定
原点固定,是因为任何矩阵与0向量相乘,都是0向量,原点始终固定。
线性变换的重要性质是,所有的变换的网格线(网格是想象中的一些向量的终点)是保持平行且等距分布的。

所有变换后的新向量,都可以通过基向量的变换进行相同的转换操作。
在一个二维转换中,我们可以把矩阵的列完全看做是变换后的基向量
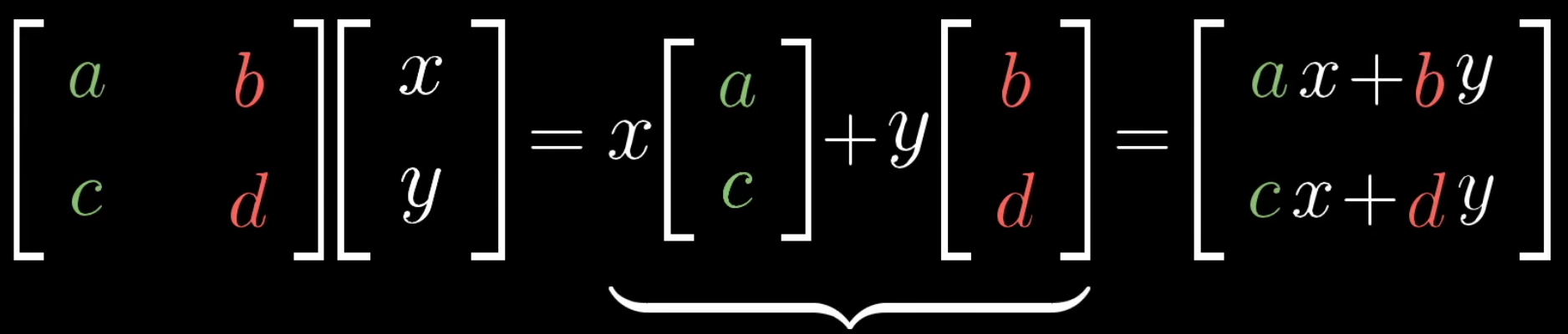
向量\([a,c]\)是变换后的基向量\(\hat{i}\),\([b,d]\)是变换后的基向量\(\hat{j}\)。
因此,linear transformation可以看做是空间的一种变换,即基向量的变换。因此,我们可以直观上把矩阵看做是对空间的变换。
4 Matrix multiplication
矩阵相乘可以看做是连续的空间变换,这也解释了为什么矩阵位置互换,结果不能保证一样。
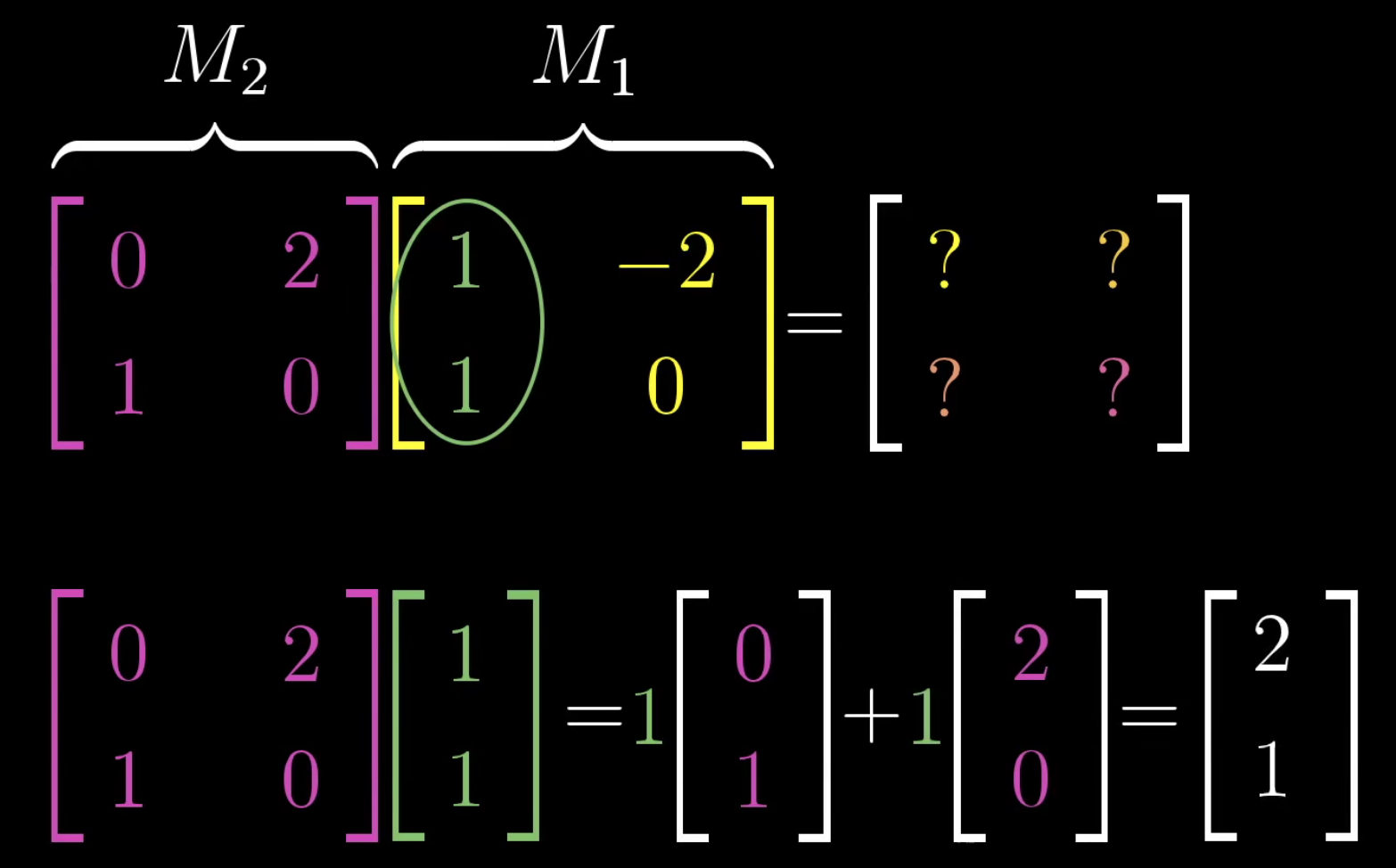
上面的矩阵\(M_2\)把矩阵\(M_1\)的列向量进行变换,矩阵\(M_1\)的列向量可以看做是新的基向量\(\hat{i}\)。
5 The Determinant
行列式determinate的几何含义,以二维平面为例,就是以单位basis向量组成的单位正方形的面积的变化。比如:

特殊的情况是determine为0:
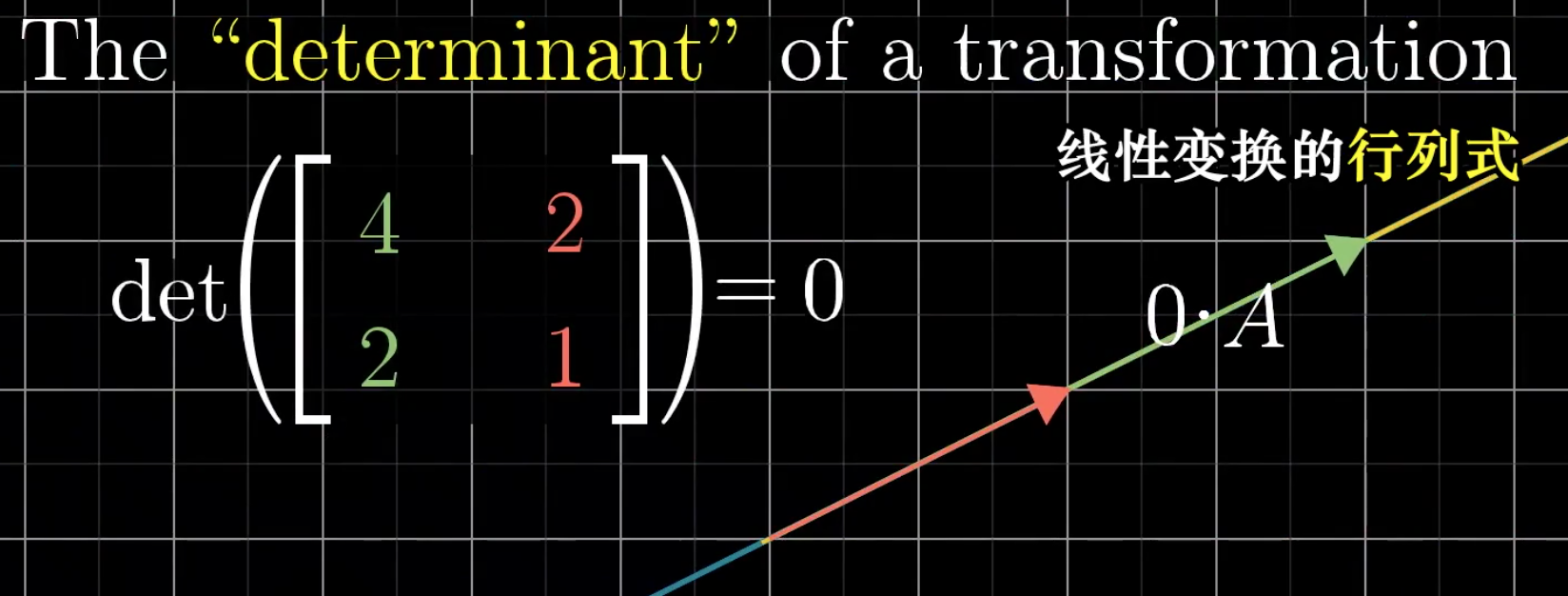
此时整个空间被压缩为一条直线,甚至是一个点。因此,如果我们计算某个matrix的行列式是否为0,我们就知道这个矩阵是否表示把空间压缩到更小的维度上。
此时还有另外的问题,那就是行列式是可以为负数的,此时,行列式代表矩阵会把空间翻转(fliping),行列式的绝对值仍然是面积的变化。
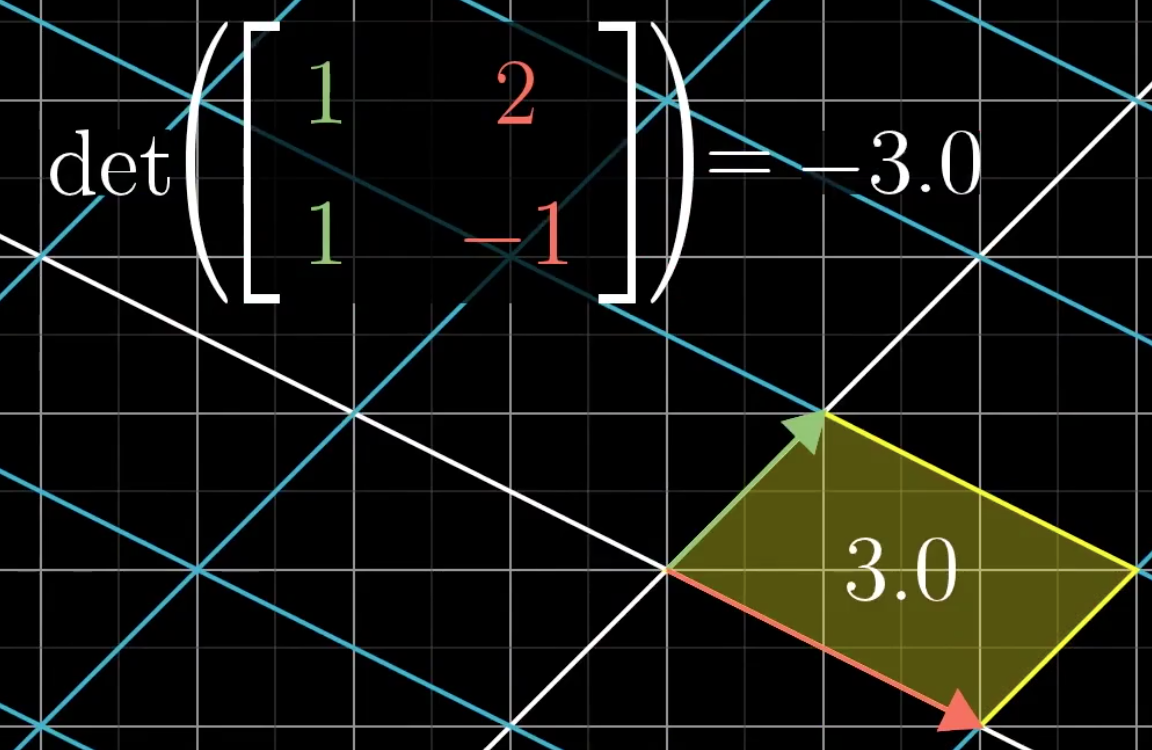
对于行列式的变换,假设\(\hat{i}\)逐渐接近\(\hat{j}\),看下面一系列的动画:
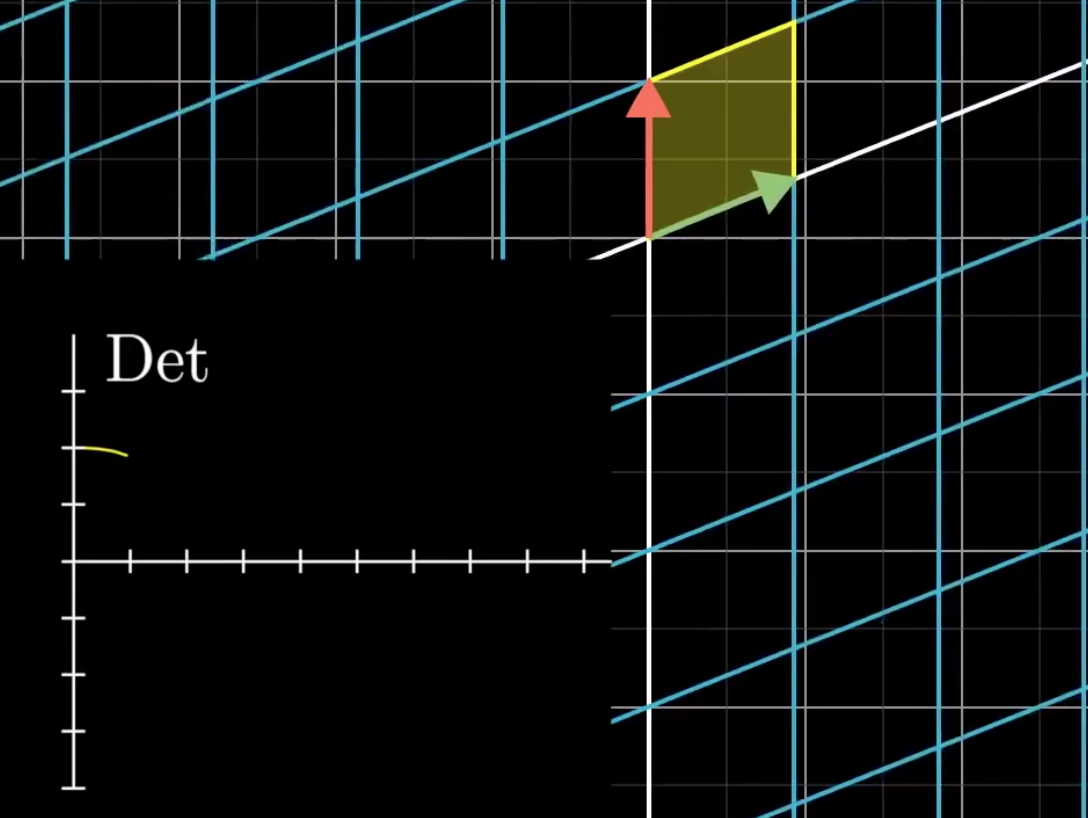
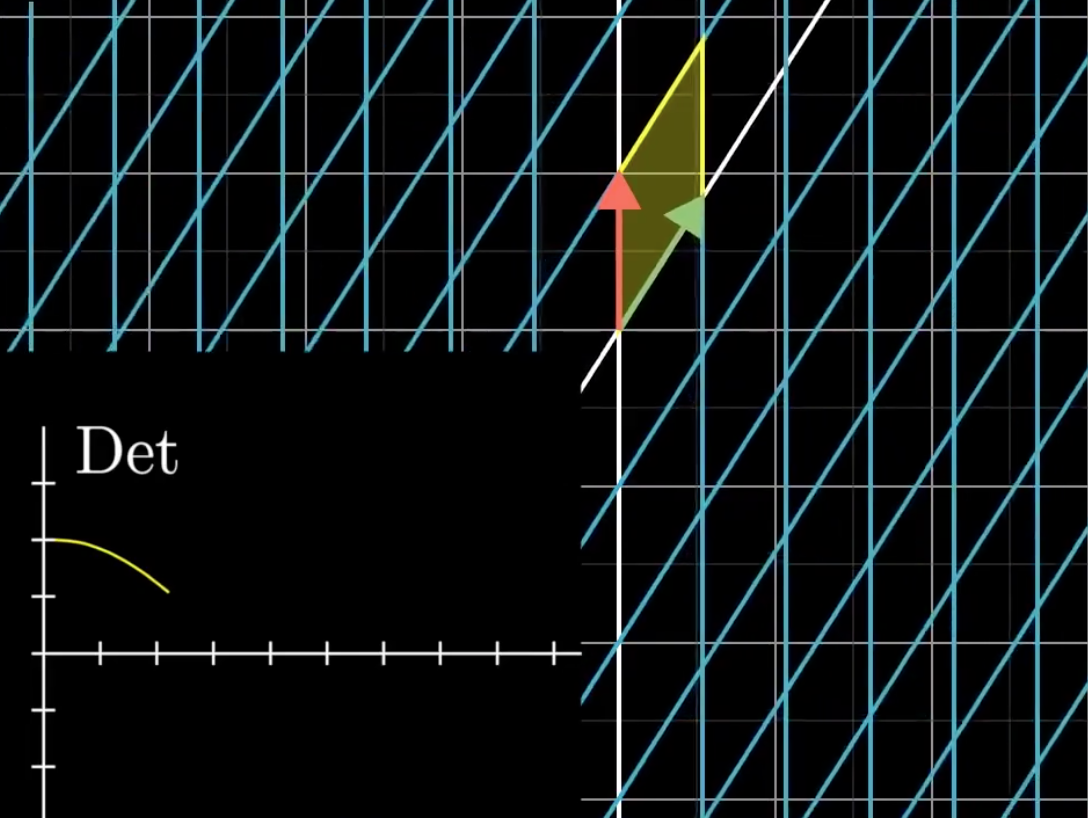
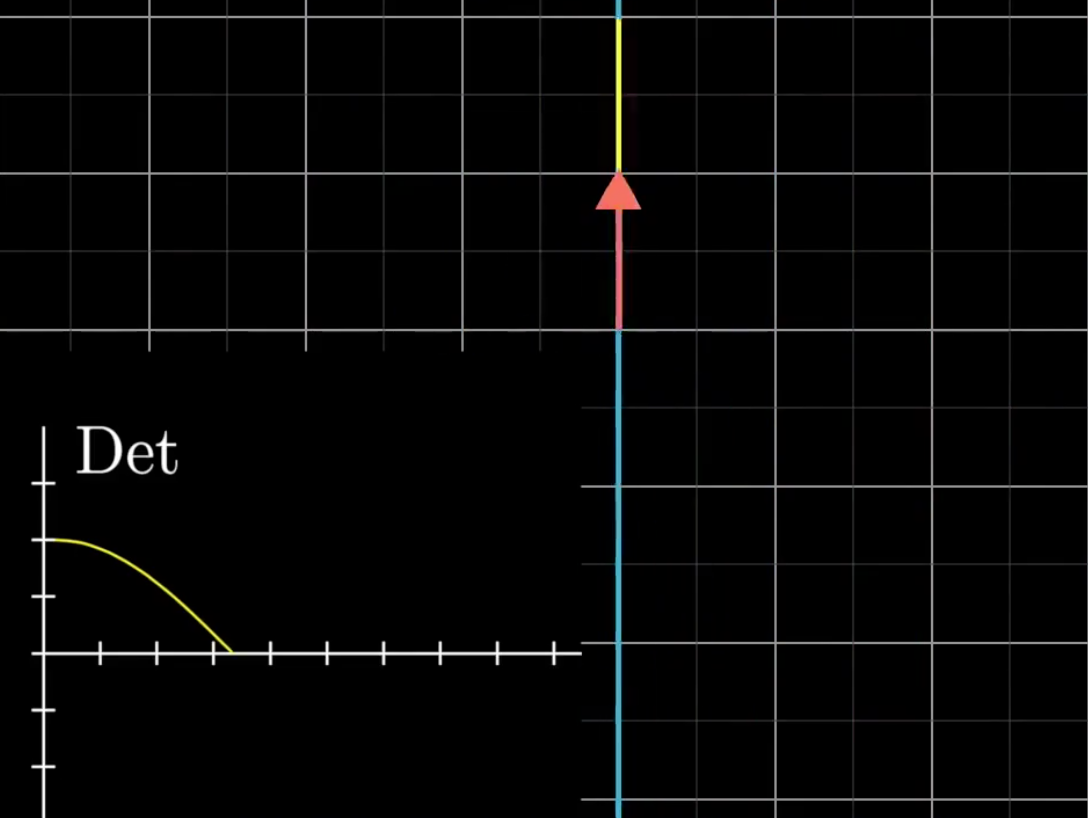
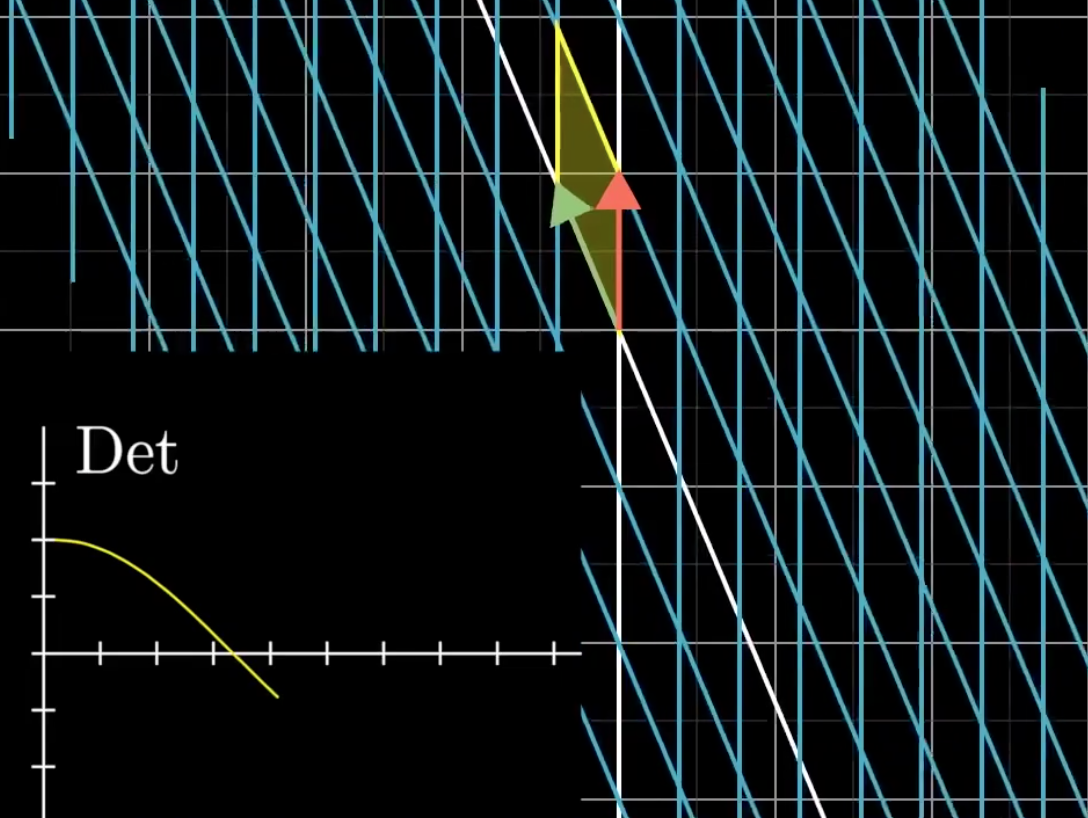
出现了负数的行列式。
如果在三维空间中,那么矩阵行列式就是单位体积的变化:
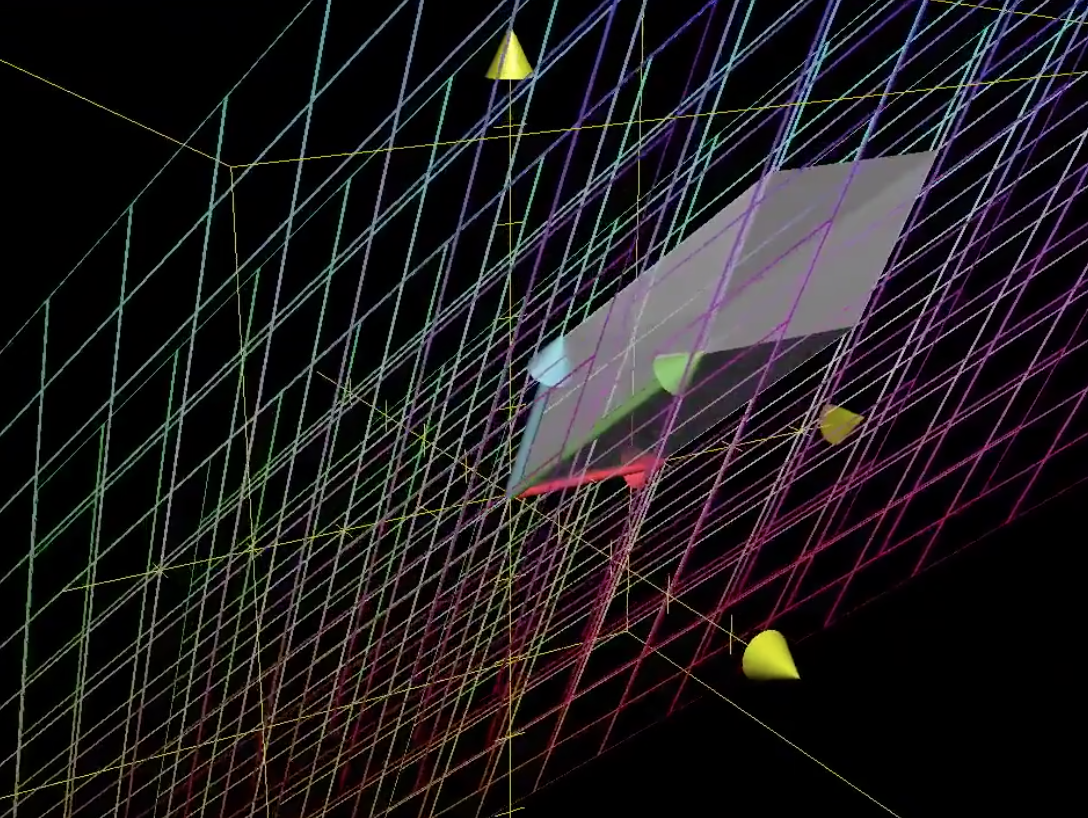
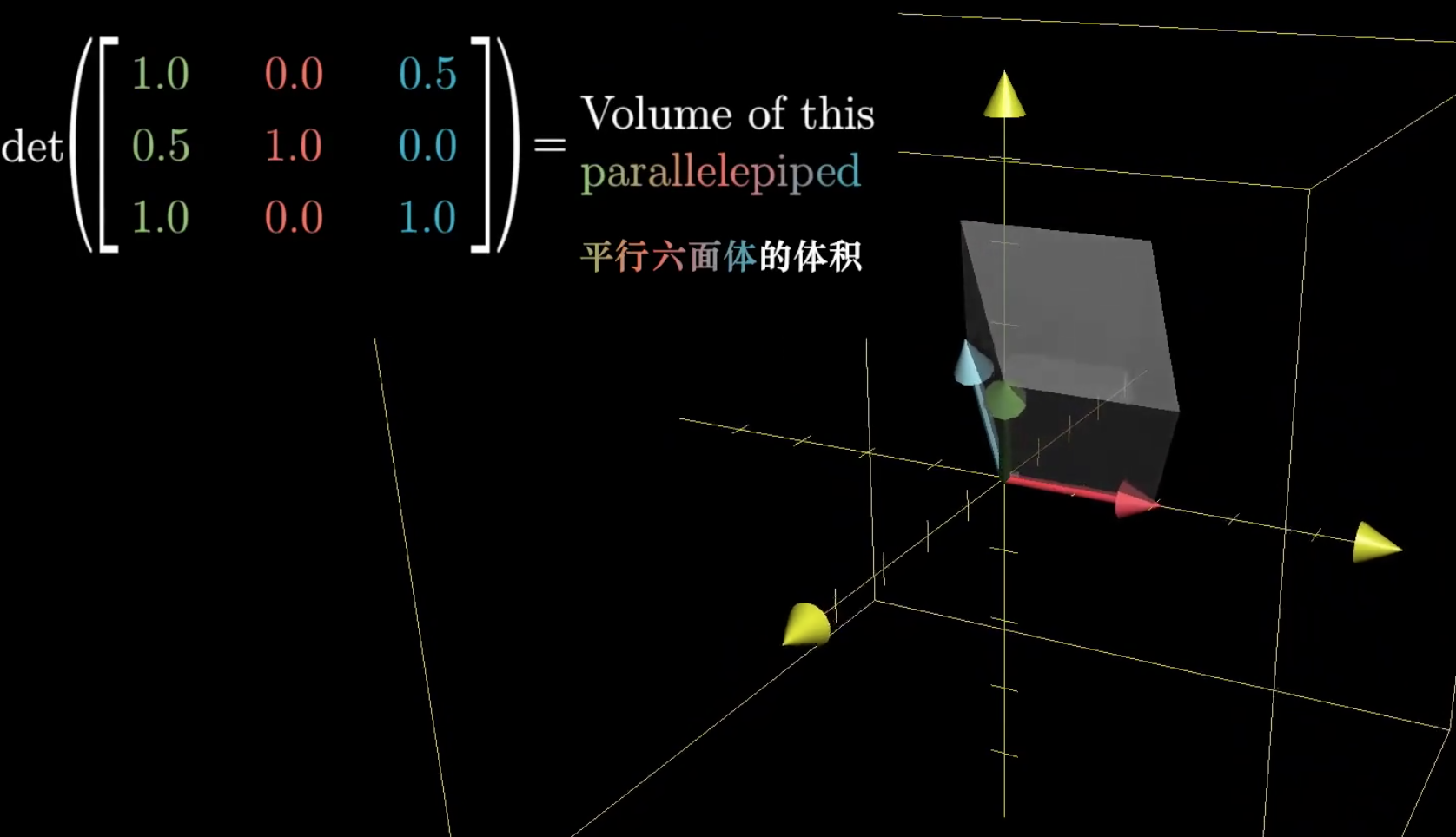
因为矩阵的列向量可以看做是新的基向量,如果行列式为0,就表示出现了列向量线性相关的情况,某个或者多个列向量可以由其它列向量表示。
行列式的计算过程,实际就是在计算这个面积/体积的变化,比如:
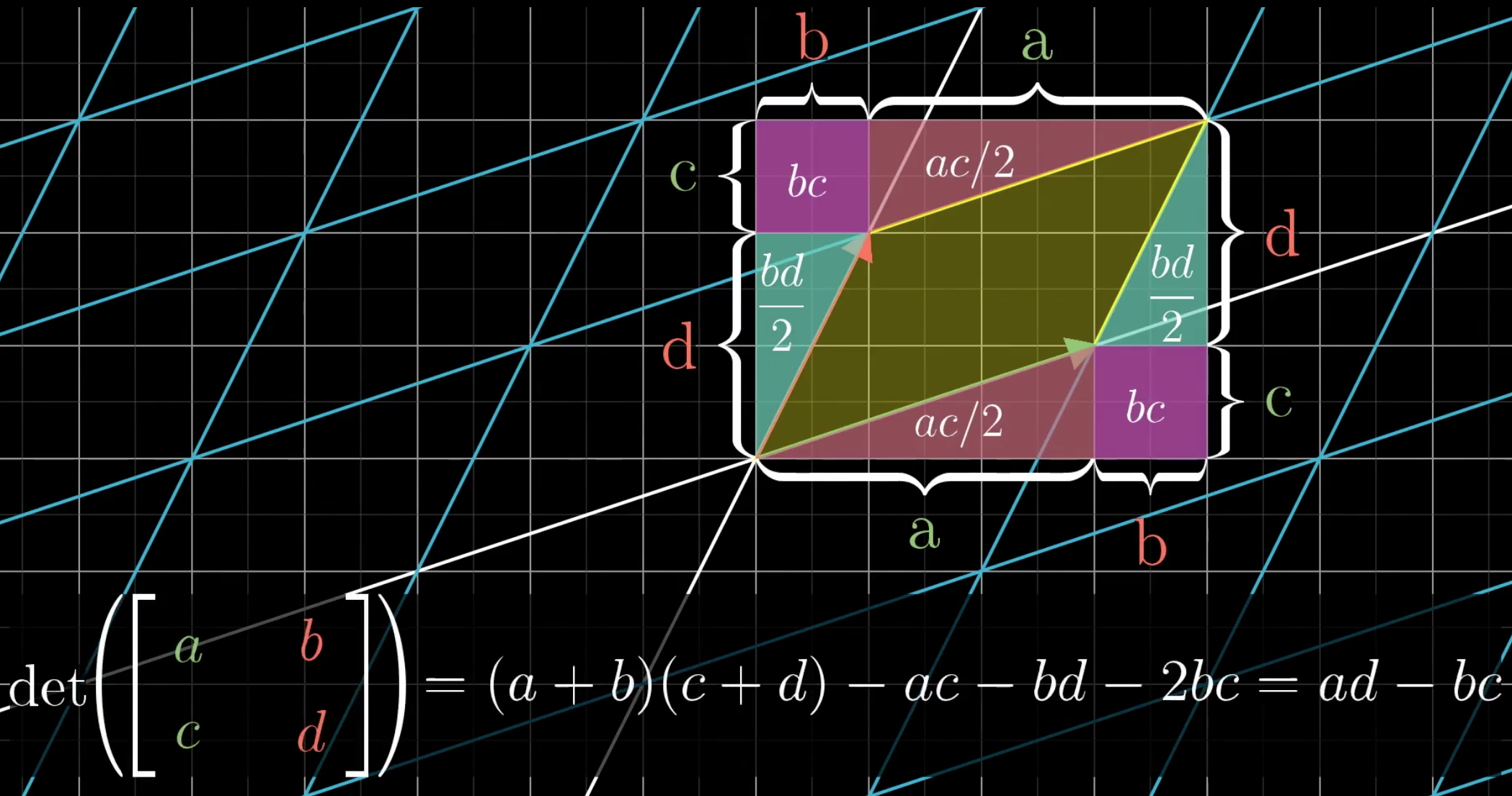
懂了行列式的几何意义,可以很轻松的理解下面的定理:

对空间进行\(M_1M_2\)然后的变换后的面积变化=先进行\(M_2\)变换,然后进行\(M_1\)变换后的面积变化。本质是一样的。
6 Inverse Matrices, column space and null space
我们都知道,对于多元一次的方程组,求解未知变量,可以用矩阵的角度来看:
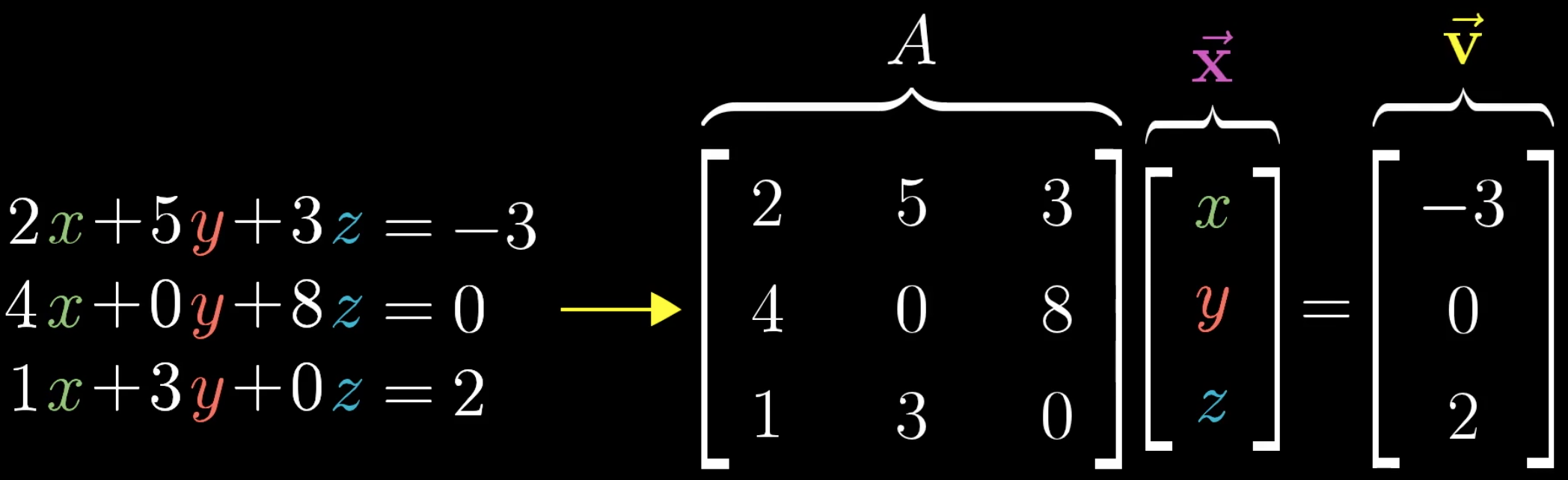
从矩阵是空间变换的角度来看,我们已知变换后的向量\(v\),只要逆着矩阵\(A\)的变换,就能够找到空间变换前的向量\(x\)。

这就是矩阵的逆矩阵\(A^{-1}\),逆矩阵乘以矩阵,表示的是什么都不做的变换,即一个单位矩阵。
只要行列式不为0,就存在对应的逆矩阵。
如果行列式为0,表示矩阵\(A\)将空间的维度进行了压缩,我们此时无法还原原来没有压缩的空间,它对应的解有无数种。
如果矩阵表示的变化,最后把空间压缩为直线,就叫做此时矩阵的秩是1。如果压缩为二维平面,矩阵的秩就是2。
rank表示变化空间后的空间维数,因此,一个矩阵最大的rank就是它本身的维数。
矩阵的列空间:

矩阵的列空间也就是变换后的空间,rank就是指列空间的维数。
矩阵的零空间null space:
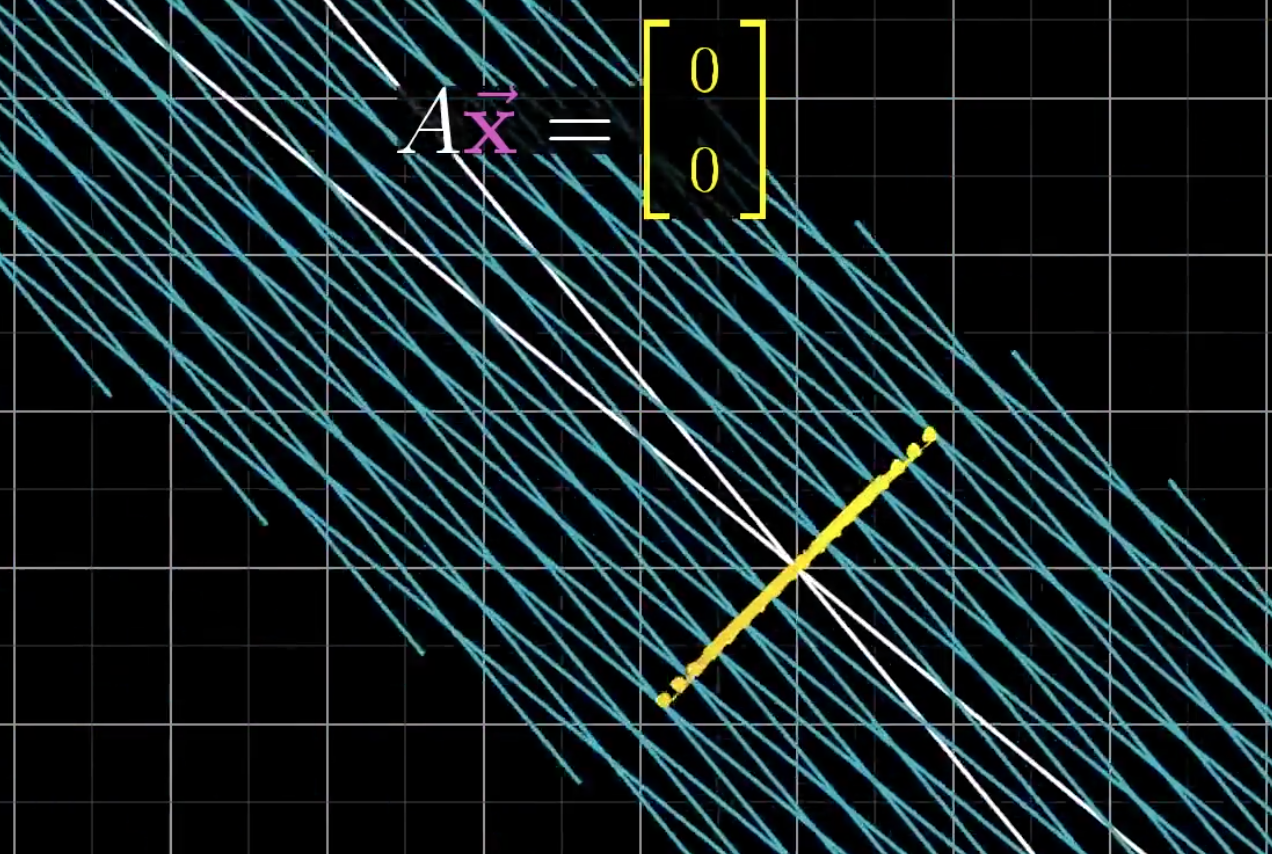
矩阵进行空间变换时,所有变换后落在原点的向量集合,组成了null space。
在线性方程组上,就是变换后的向量是0向量:
7 Nonsquare matrices as transformation between dimensions
前面讨论的都是方阵,如果是一个非方阵,那么表示的是维度的变化,比如从二维变换为三维,三维变化为二维。
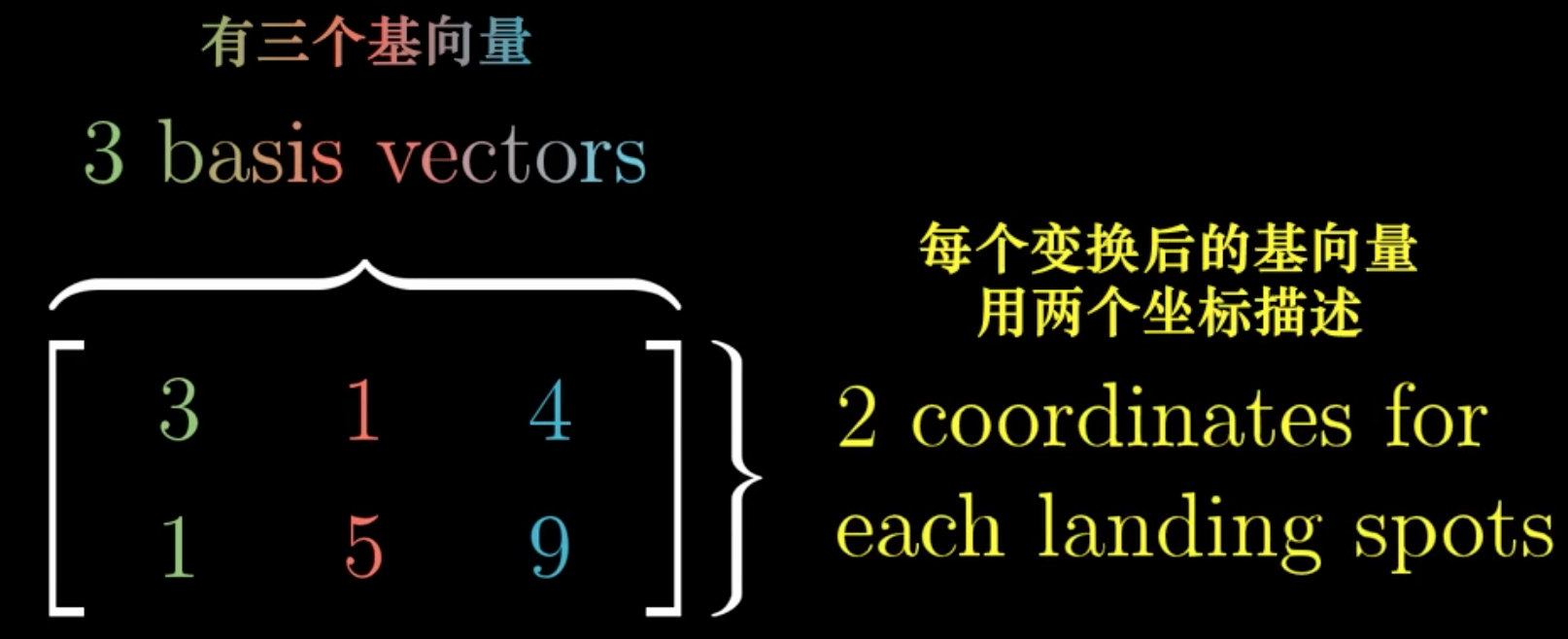
上面的矩阵就是从三维,变化到二维,列表示的基向量,从三维被表示为二维的向量,但是由于原来是三维空间,所有仍然有三个基向量。
8 Dot products and Duality
向量的点积就是所有维度的元素相乘然后相加。
如果希望从几何角度来理解,可以把左边的向量\(u\)转置,变为矩阵的形式:

此时,从几何角度来看1维矩阵的变换,因为对称性,新的基向量\(\hat{i}\)刚好是\(u_x\),新的基向量\(\hat{j}\)刚好是\(u_y\)。使用新的变换矩阵作用在向量\([x, y]^T\)上,就是对其进行和对投影的变化操作。

9 Cross products
差积的定义:
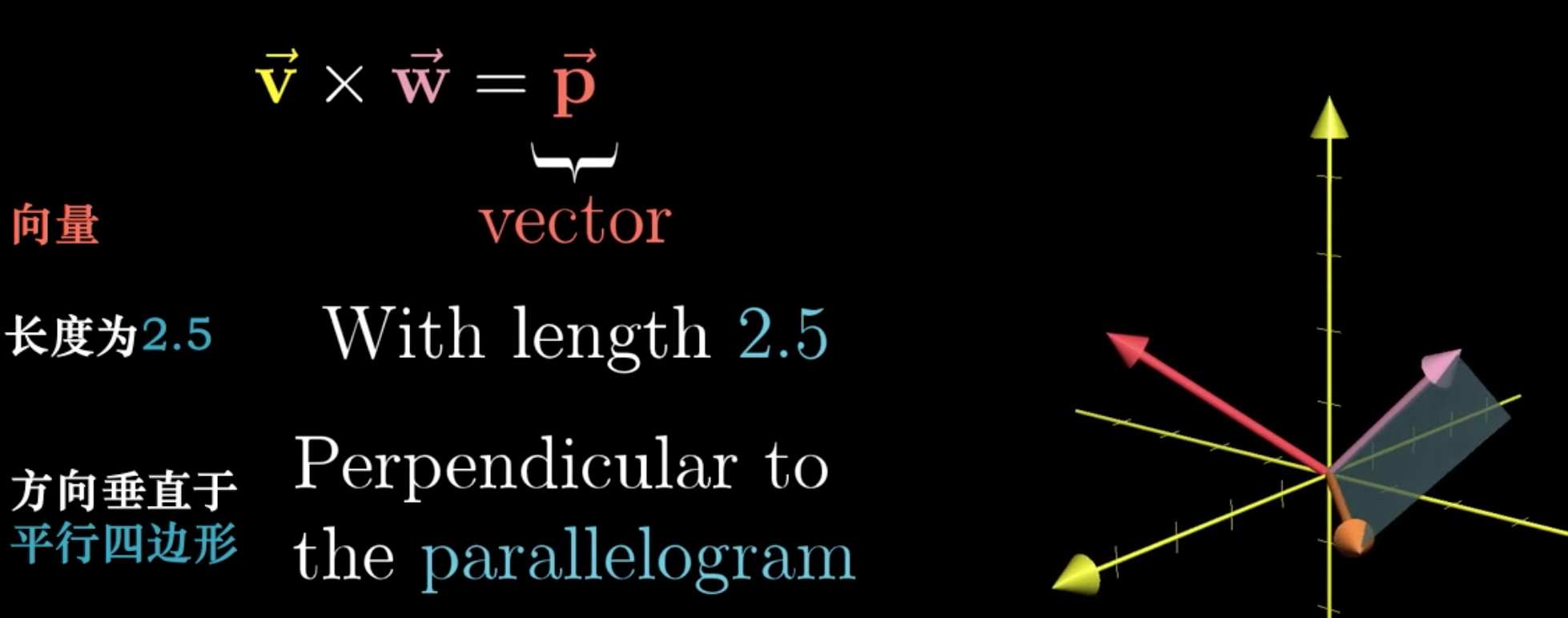
一个新的向量,长度是\(v\)和\(w\)组成的平行四边形的面积,方向垂直于该平行四边形。
该平行四边形面积的计算,可以使用\(v\)和\(w\)组成矩阵,然后求该矩阵的行列式。
10 Change of basis
当我们定义了不同的基向量来描述空间中的同一个向量时,即使是同一个向量,也会使用不同的坐标来描述。
一个矩阵的列向量可以看做是新的基向量,它描述的是另一个坐标系的基向量,在我们想象当中的坐标系中的表示,
比如下面的形式:
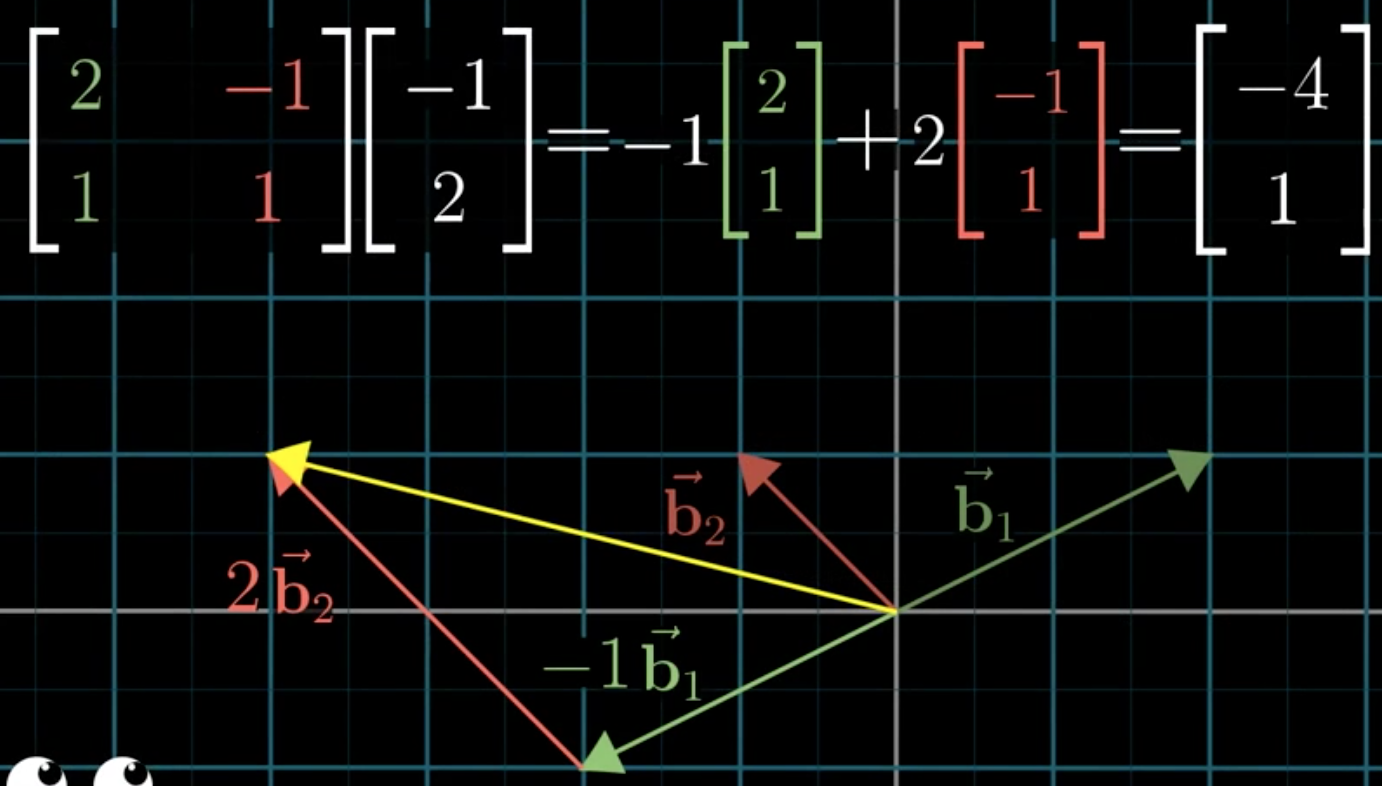
\([2,1]\)和\([-1, 1]\)是另外的坐标系的基向量,但是如果在另外的坐标系中,它实际表示的是\([1,0]\)和\([0,1]\)。我们使用自己的语言/坐标系来描述另一个坐标系的基向量。坐标\([-1,2]\)是在另一个坐标系下的坐标。


如果我们是希望自己坐标系下的\([-1,2]\),被转换到另一个坐标系中,那么我们可以用逆矩阵进行转化。

接下来,如果我们在自己的坐标系下,使用矩阵,进行了一个空间变化/基向量的线性转换,那么在另一个坐标系下,进行相同的转化的矩阵应该是什么?
实际上,我们只需要首先,把另一个坐标系下的基向量变换到自己的坐标系下,然后进行要求的空间变换,最后通过逆矩阵再变换到另一个坐标系下。


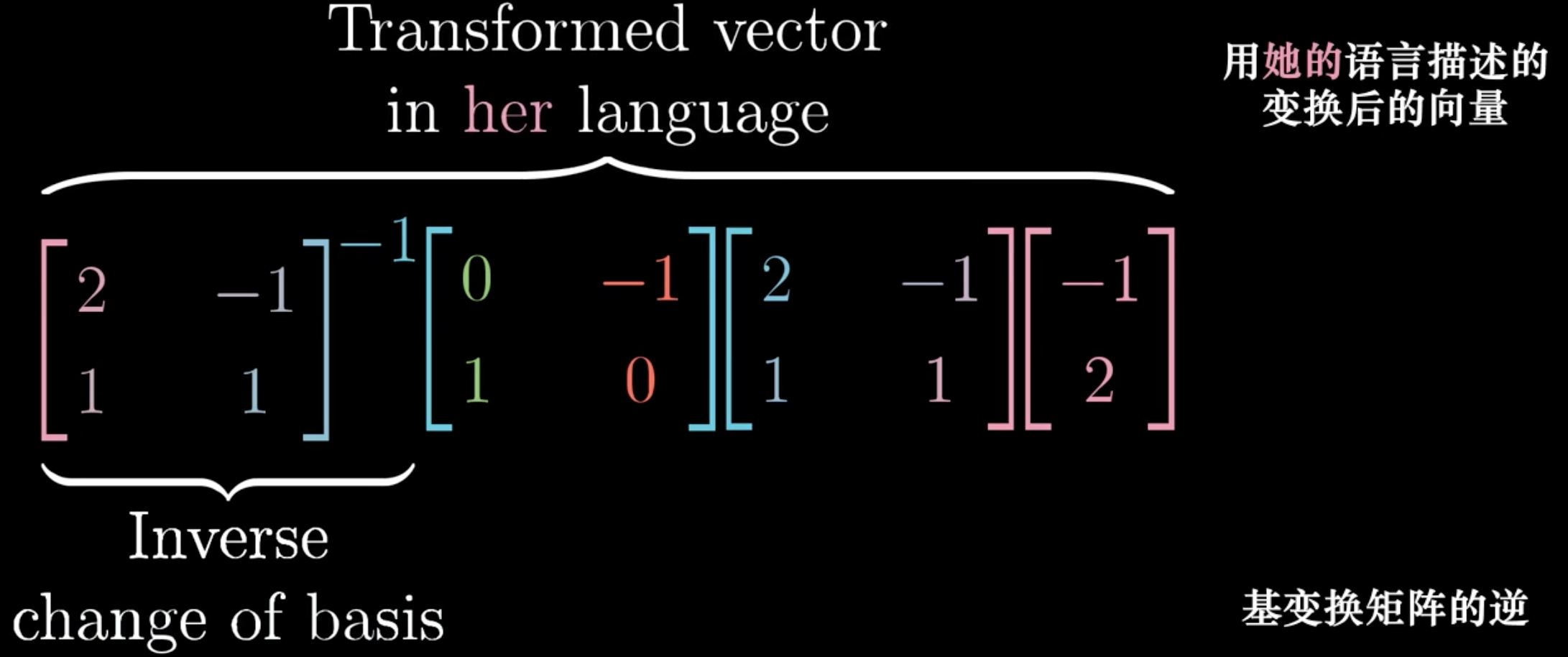
因此,如果我们看到下面的形式,我们可以直接从中间矩阵\(M\)来看发生了什么变化,左右两侧的矩阵表示空间基向量坐标的转化:

11 Eignvectors and eigenvalues
如何从几何角度理解特征值和特征向量?
还是假设在一个空间坐标中,进行了空间变换。
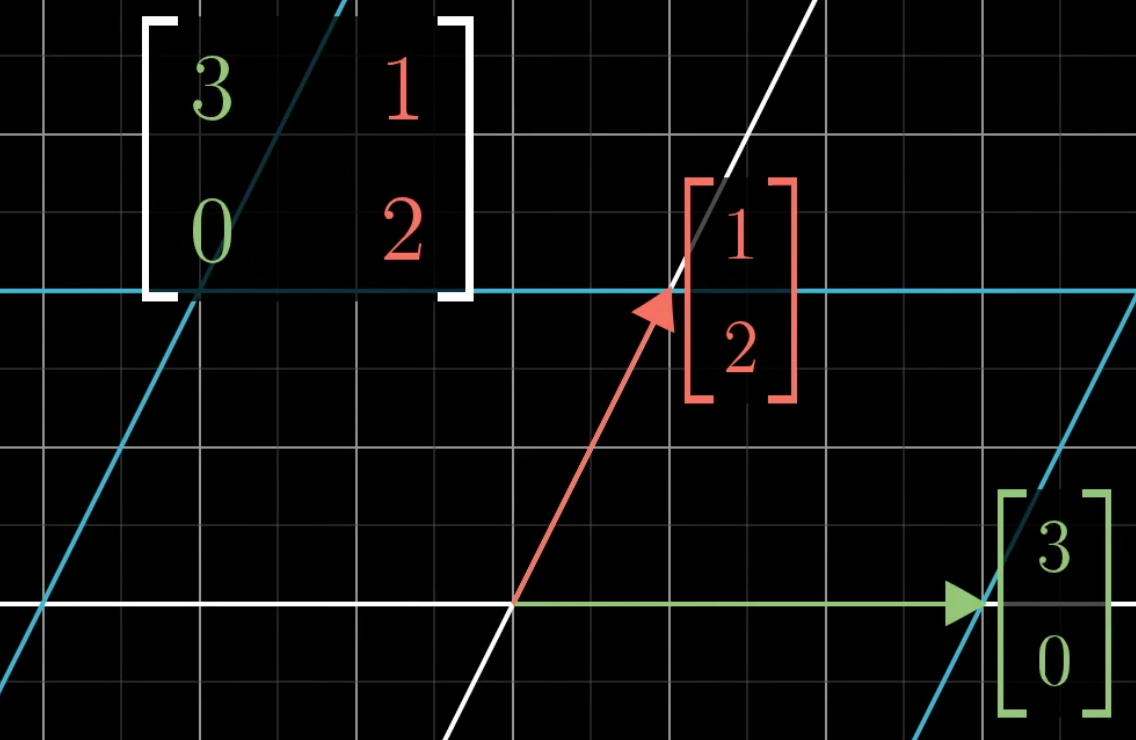
在进行这个空间变换中,大多数的向量都会发生一个角度的偏移,即和原来的向量不在一条直线上。但是有一些向量是和原来的向量还在一条直线上,对于这些向量来说,空间的变换仅仅是发生了长度的缩放,比如说对于所有在x轴上的向量来说,仅仅是长度增长三倍。
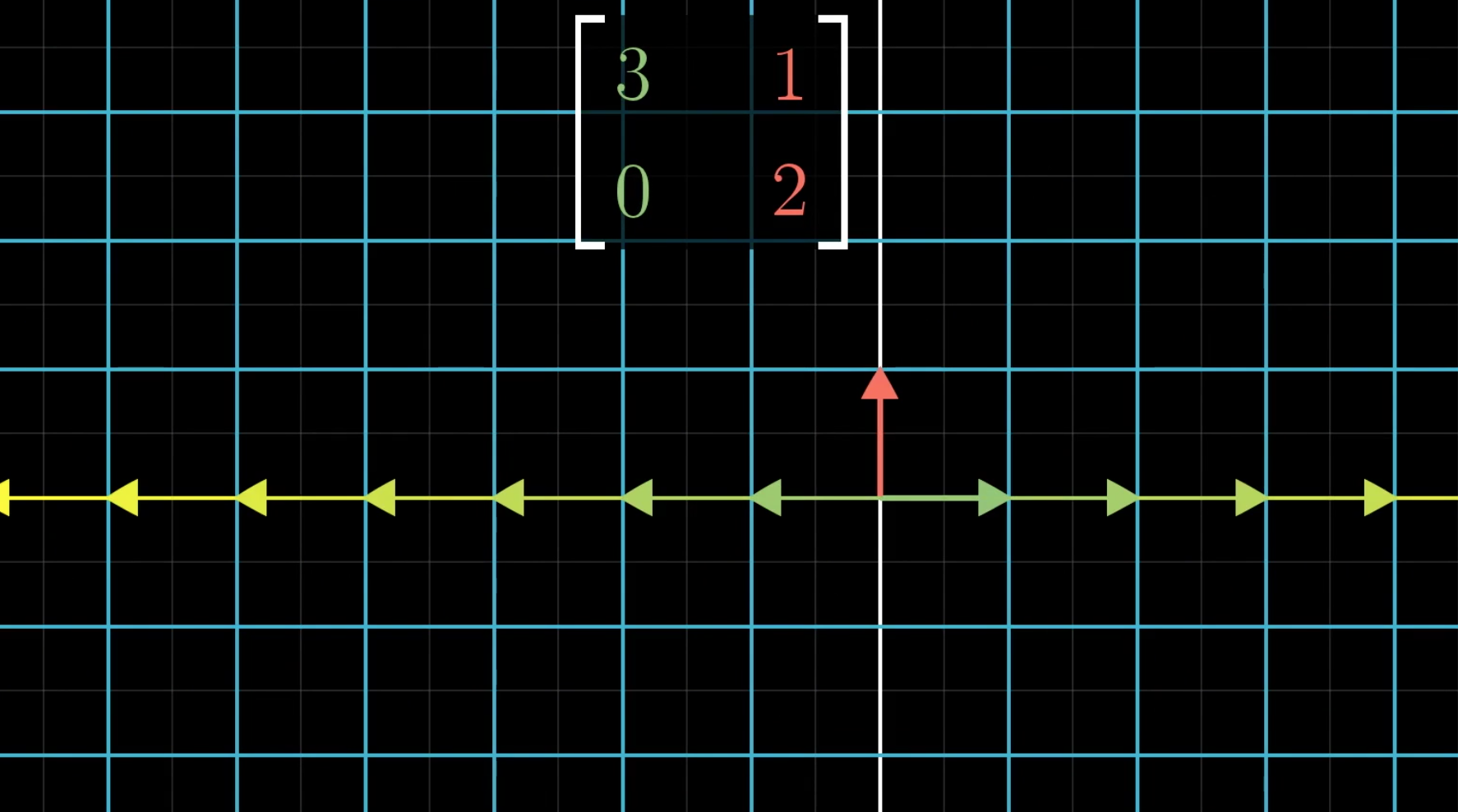
还存在其它的向量,也是类似的只会进行长度的缩放
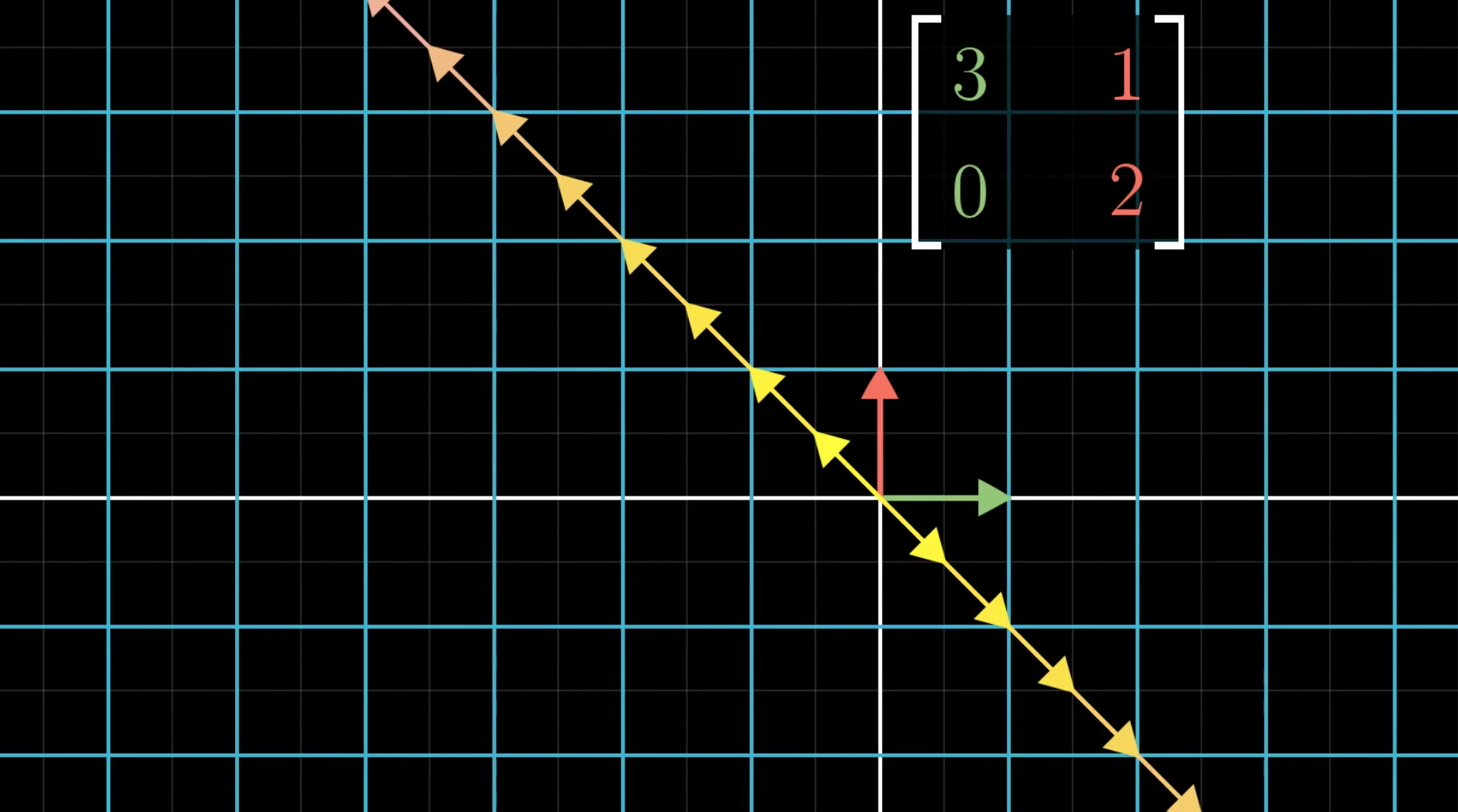
这些向量就叫做特征向量,需要进行的长度缩放就叫做特征值。

求解特征向量与特征值的一般过程:
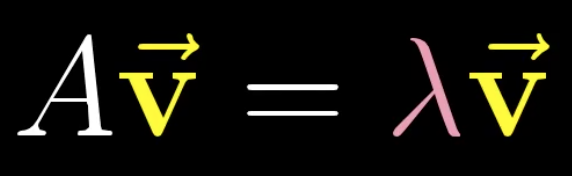

根据前面的矩阵是空间变换可知,如果希望把一个向量通过矩阵空间变化,压缩为0向量,那么只有可能是行列式为0。
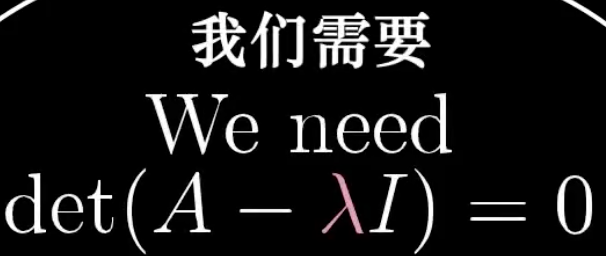
当然,这样的性质表明了不是所有的矩阵都会有特征值,有的矩阵会把所有的向量都进行旋转操作,也就不存在特征向量了。
对应特征值的特征向量不一定就在一条直线上,最简单的,考虑一个矩阵是将所有向量都扩放到2倍。那么对于特征值2的特征向量就是整个空间下的所有向量。

接下来,看一下由特征向量为基,组成的特征空间的作用。
对于一个矩阵,如果它的特征向量有多个,可以组成一个全空间,那么以这些特征向量作为新的基向量,如果我们将这个新的特征基组成的basis change矩阵作用在原始矩阵上:

我们知道,这样得到的新矩阵,和之前的矩阵对于空间中的向量来说是同一种变换,但是是从新的特征空间下看的。这样得到的新的变换矩阵 ,在特征空间下,一定是对角矩阵,对角值是特征值。
这是因为,整个原始矩阵的空间变换,对于新的特征空间下的作为基向量的特征向量来说,仅仅是起到了缩放的作用,所以新的特征空间下的矩阵变换,就是对角矩阵,只有长度进行了缩放。
12 Abstract vector spaces
线性转换的概念不仅局限在向量上,对于函数同样存在这样的定义:
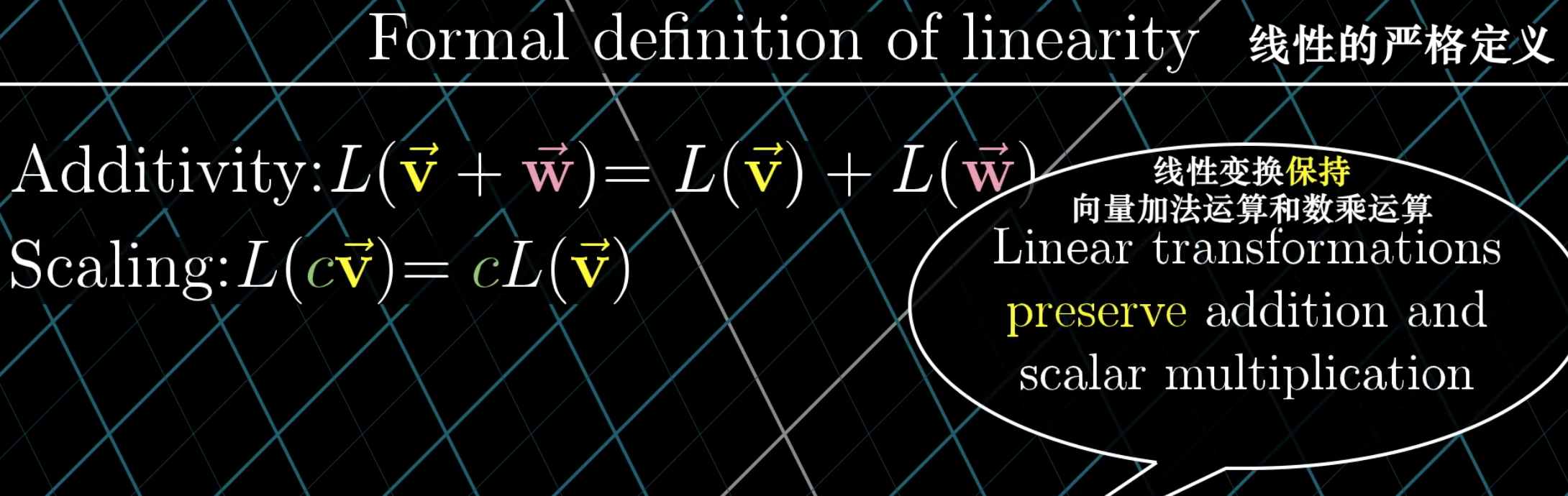
求导运算,实际就是一种线性运算。


实际上,向量的很多概念是可以应用到函数上的。

向量的类似概念是可以推广到进行了任意定义的对象的,只要定义的数乘运算和相加运算,能够满足下面的checklist,就可以认为此时定义的新的运算,可以组成一个向量空间,可以使用向量的各种相关概念去思考,定义。
