linear-algorithm-in-ICL

What learning algorithm is in-context learning? Investigations with linear models

ICLR 2023, Google Research and MIT, 地址。

Neural sequence models, especially transformers, exhibit a remarkable capacity for in-context learning. They can construct new predictors from sequences of labeled examples (x, f(x)) presented in the input without further parameter updates. We investigate the hypothesis that transformer-based in-context learners implement standard learning algorithms implicitly, by encoding smaller models in their activations, and updating these implicit models as new examples appear in the context. Using linear regression as a prototypical problem, we offer three sources of evidence for this hypothesis. First, we prove by construction that transformers can implement learning algorithms for linear models based on gradient descent and closed-form ridge regression. Second, we show that trained in-context learners closely match the predictors computed by gradient descent, ridge regression, and exact least-squares regression, transitioning between different predictors as transformer depth and dataset noise vary, and converging to Bayesian estimators for large widths and depths. Third, we present preliminary evidence that in-context learners share algorithmic features with these predictors: learners’ late layers non-linearly encode weight vectors and moment matrices. These results suggest that in-context learning is understandable in algorithmic terms, and that (at least in the linear case) learners may rediscover standard estimation algorithms.

1. Introduction

这篇工作的研究问题：How can a neural network with fixed parameters to learn a new function from a new dataset on the fly?

作者做了这样的假设，上下文学习过程中，Transformer潜在的学习到了一个映射函数，并且上下文中的样例起到了对这样的潜在函数进行训练的作用。

This paper investigates the hypothesis that some instances of ICL can be understood as implicit implementation of known learning algorithms: in-context learners encode an implicit, context-dependent model in their hidden activations, and train this model on in-context examples in the course of computing these internal activations.

2. Preliminary

The Transformer architecture

作者研究的是Transformer的decoder，下面是self-attention定义：

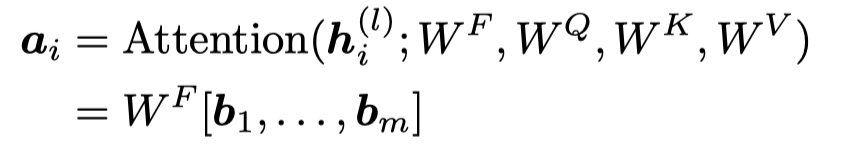
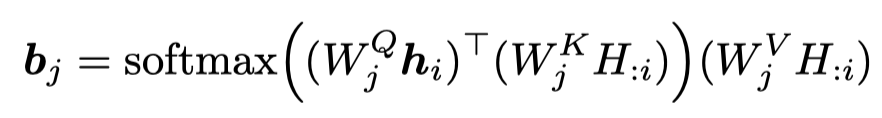
下面是feed-forward transformation的定义：

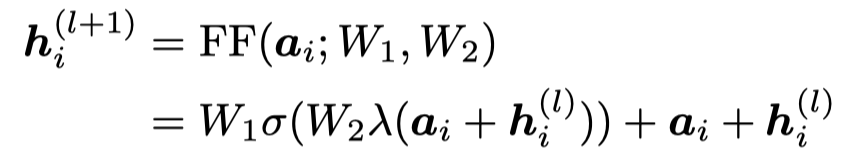
其中的\(\lambda\)是layer normalization，\(\sigma\)是GeLU等激活函数。

Transformer的computational capacity与depth，hidden size \(h\), number of heads \(m\)有关。

Training for in-context learning

作者在论文中讨论的Transformer，是针对ICL objective进行优化的模型。不是目前更多的单纯优化language objective的LM：

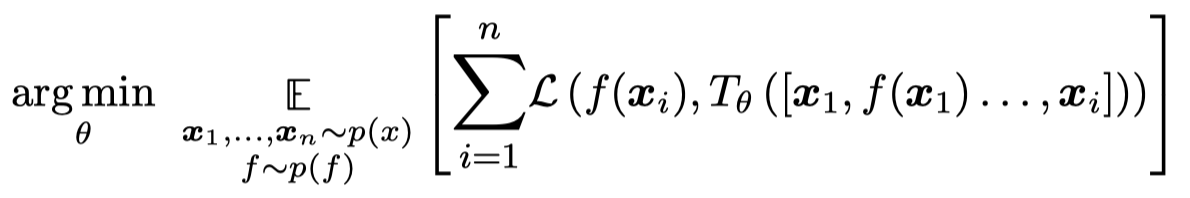
单纯的看这个loss，感觉是先输入上下文exemplar 1，预测exemplar 1，计算loss；然后输入exemplar 1和exemplar 2，预测exemplar 2，计算loss。

Linear regression

作者对比的learning algorithm是linear regression，原因之一是linear regression相对简单，人们对于它的理解比较充分。

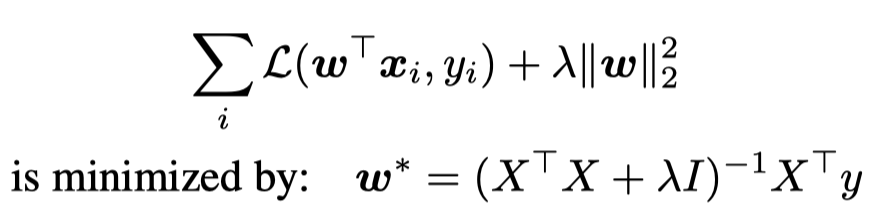
当\(\lambda=0\)，上面的回归称为ordinary least squares regression (OLS)；

当\(\lambda>0\)，上面的回归称为ridge regression岭回归。

其中的\(w^*\)表示线性回归的最优解。

3. What learning algorithms can a transformer implement?

这一部分，作者证明从理论上，通过固定Transformer中self-attention层和FFN层的一些参数，可以让Transformer实现linear regression。

for \(d\)-dimensional regression problems, with \(O(d)\) hidden size and constant depth, a transformer can implement a single step of gradient descent; and with \(O(d^2)\) hidden size and constant depth, a transformer can update a ridge regression solution to include a single new observation. Intuitively, \(n\) steps of these algorithms can be implemented with \(n\) times more layers.

3.1 preliminaries

作者定义了下面的几种变化操作，然后证明Transformer可以实现这些操作：

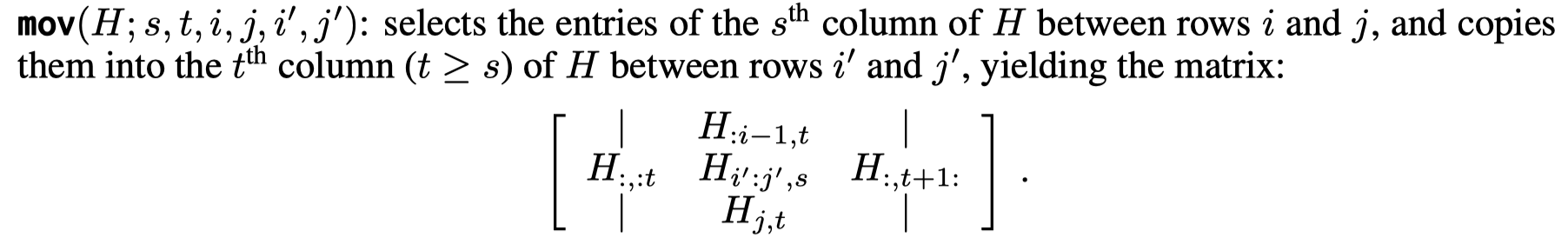
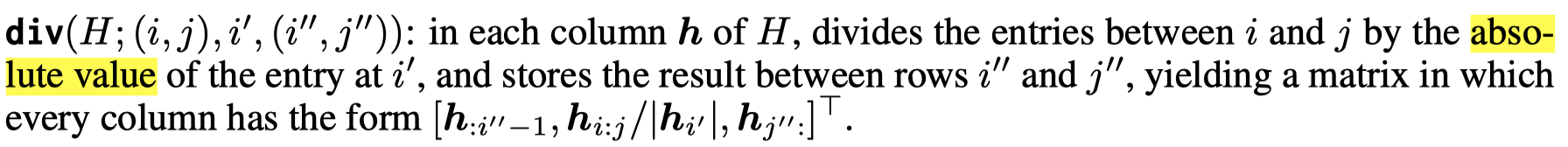
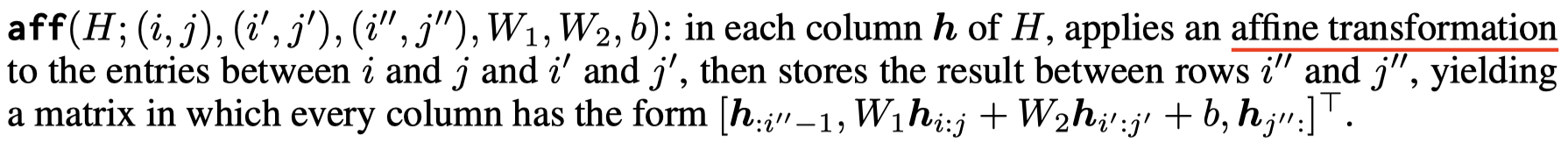
证明过程在附录。

下面是作者的引理：

下面两个部分，是作者讨论的两种学习linear model参数的方法。作者从理论上证明Transformer能够学习这样的映射函数。

3.2 Gradient descent

通过梯度下降的形式学习linear model的参数：

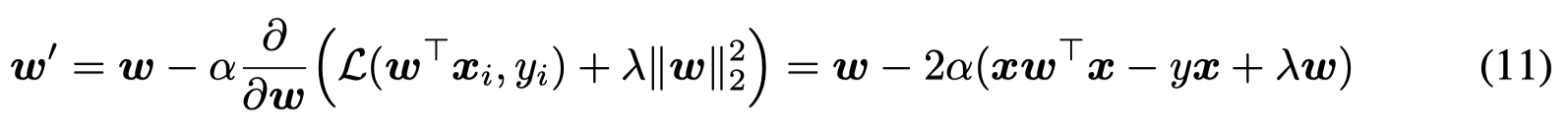
然后，作者证明从理论上，在最后输出的对应\(x_n\)（测试样例）的结果，某一个元素可以等于线性回归的计算结果：

3.3 Closed-form regression

直接计算最优解\(w^*\)需要计算\(X^TX+\lambda I\)的逆矩阵，这种计算比较复杂。

然后作者利用Sherman–Morrison formula [Adjustment of an inverse matrix corresponding to a change in one element of a given matrix. 1950]可以将这种求方阵\(A\)的逆矩阵转换为迭代的和rank-one的example进行运算的方法：

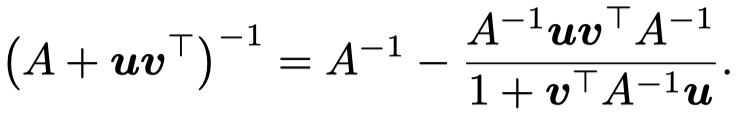
最后，被转化的求\(w^*\)的方法：

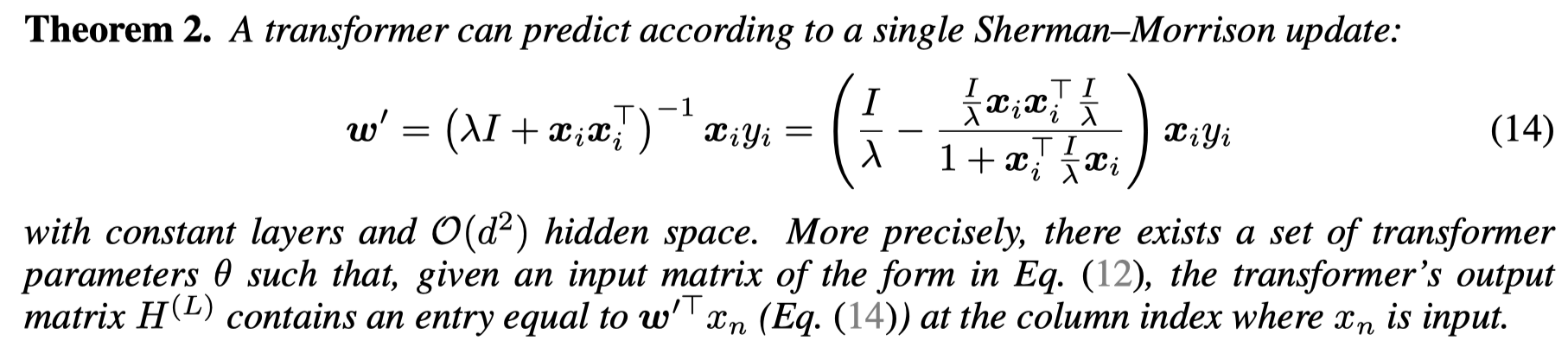
4. What computation does an in-context learner perform?

这一部分是从实验中评估，Transformer对于上下文的处理和linear model在多大程度上是相近的。

4.1 Behavioral metrics

首先是要定义度量指标，作者定义了两个metric，Squared prediction difference（SPD）和Implicit linear weight difference（ILWD）。

SPD指标比较两种mapping function在预测输出的差异；ILWD比较两种mapping function的参数的差异。

4.2 Experimental Setup

作者讨论的Transformer不是特别大：

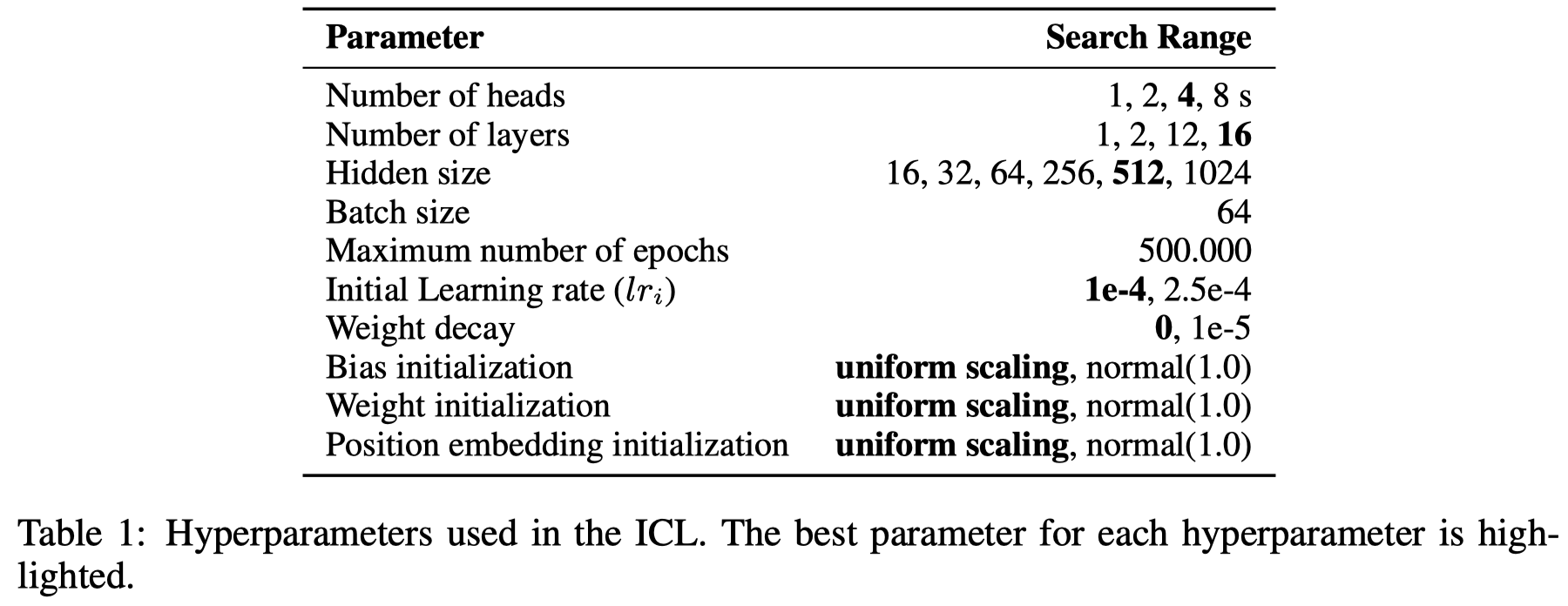
训练数据是生成的，For the main experiments we generate data according to \(p(w) = N(0, I)\) and \(p(x) = N(0, I)\).

4.3 Results

作者对比了下面几种学习算法：

包括使用欧式距离的k-NN算法、一个样本的随机梯度下降、batch随机梯度下降和直接计算最优参数\(w^*\)的方法。

ICL matches ordinary least squares predictions on noiseless datasets.

对比结果：

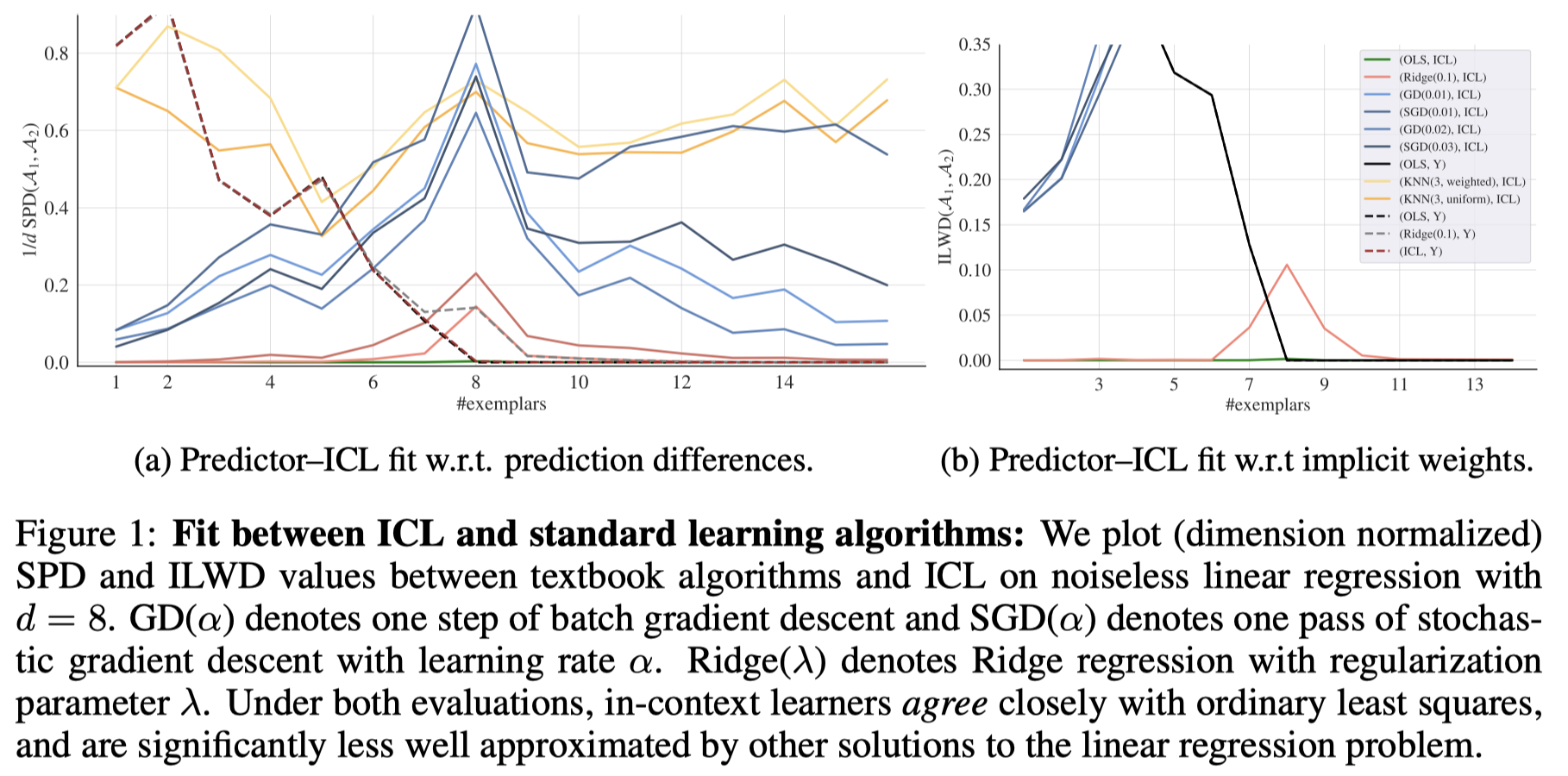
观察：

• ICL的行为和k-NN最不相似
• ICL的行为和没有正则项的线性回归最相似
• 虽然上下文样例数增多，基于梯度下降的线性回归算法也越来越靠近ICL的行为

ICL matches the minimum Bayes risk predictor on noisy datasets.

在前面的实验结果中，作者发现，Transformer的输出总是和最小二乘算法的输出一致；作者认为原因是在构造训练数据的时候，是以0位平均数的高斯分布进行采样的。Transformer通过ICL学习到了这样的规律，总是试图输出minimum Bayes risk的solution。

因此，作者构造了另外一个带有噪音的数据：

To more closely examine the behavior of ICL algorithms under uncertainty, we add noise to the training data: now we present the in-context dataset as a sequence: \([x_1 , f(x_1) + \epsilon_1 , \dots, x_n , f(x_n ) + \epsilon_n ]\) where each \(i ∼ N(0, \sigma^2)\).

最小Bayes risk的solution应该是：

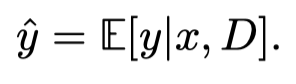
此时的最优参数应该是：

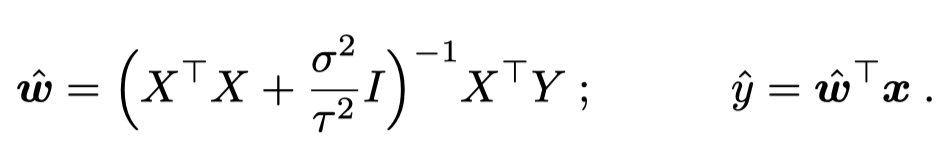
实验结果：

ICL exhibits algorithmic phase transitions as model depth increases.

作者进一步探究model size是如何影响这种内在的学习机制的：

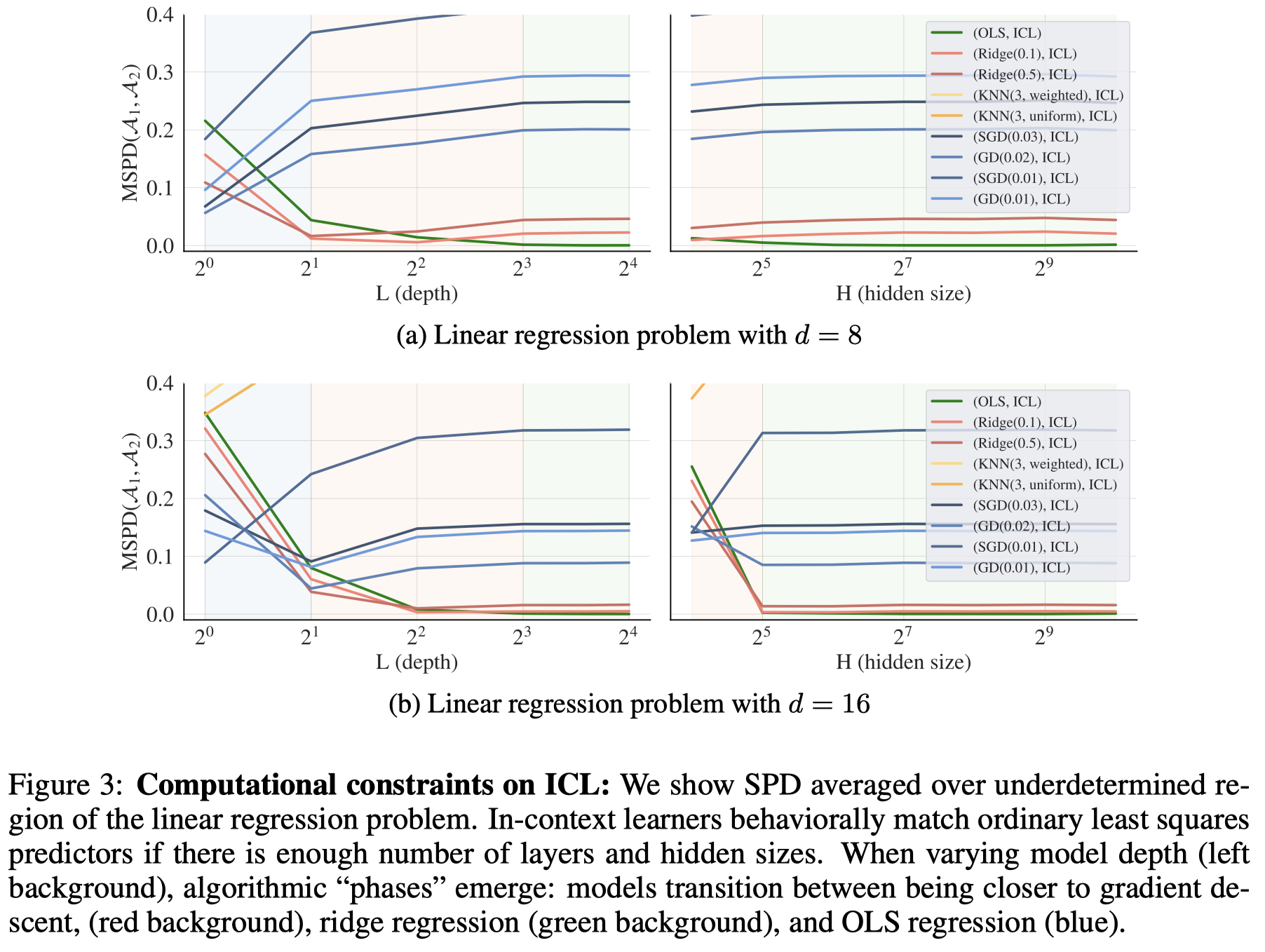
观察：

When we vary the depth, learners occupy three distinct regimes: very shallow models (1L) are best approximated by a single step of gradient descent (though not wellapproximated in an absolute sense). Slightly deeper models (2L-4L) are best approximated by ridge regression, while the deepest (+8L) models match OLS

5. Does ICL encode meaningful intermediate quantities?

最后，作者探测下Transformer的中间状态到底在编码什么样的信息？asking what information is encoded in these states, and where. 也就是希望能够理解Transformer是如何最终逐步学习到前面讨论的linear model的？

作者选择了优化linear model中要用的两个中间量作为期望被编码的信息：

• the moment vector \(X^T Y\) (gradient descent variant)
• the (min-norm) least-square estimated weight vector \(w_{OLS}\) (ridge-regression variant)

作者认为中间变量会Transformer逐步的进行编码。

为了验证这一点，训练了一个额外的an auxiliary probing model [Understanding intermediate layers using linear classifier probes. 2016]，：

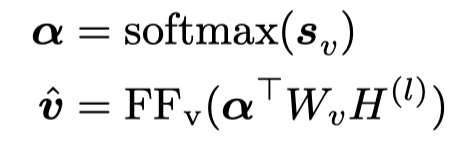
输入是前面训练的参数固定的Transformer。期望输出的\(\hat{v}\)能够逼近中间量： \[ L(v, \hat{v} ) = |v - \hat{v} |^2 \] 实验结果：

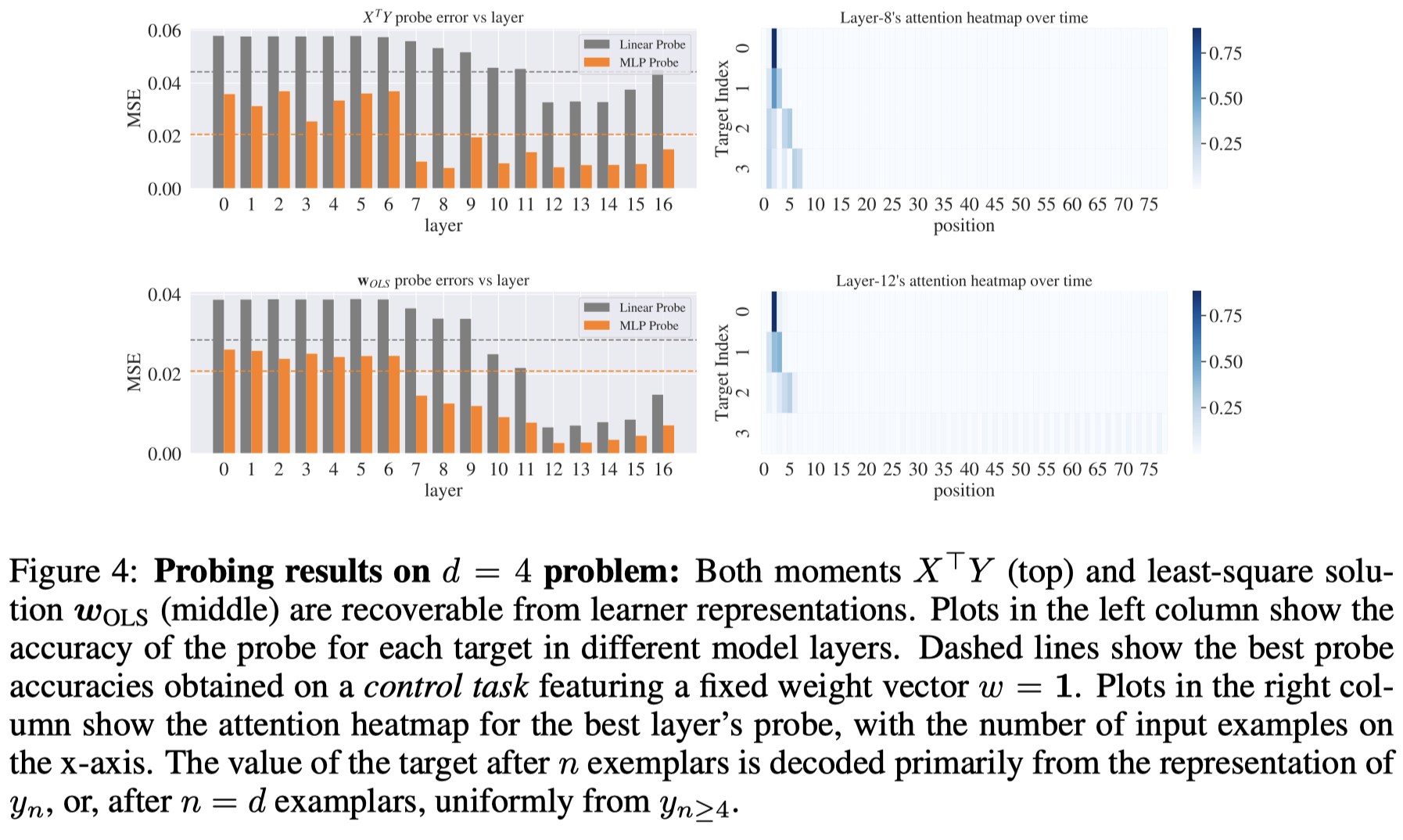
观察：

• For both targets, a 2-layer MLP probe outperforms a linear probe, meaning that these targets are encoded nonlinearly 中间量需要非线性编码

• Both targets are decoded accurately deep in the network (but inaccurately in the input layer, indicating that probe success is non-trivial.) 只有深度网络才能越来越好的学习中间量