MR-GCN
MR-GCN: Multi-Relational Graph Convolutional Networks based on Generalized Tensor Product
IJCAI 2020
2020-7
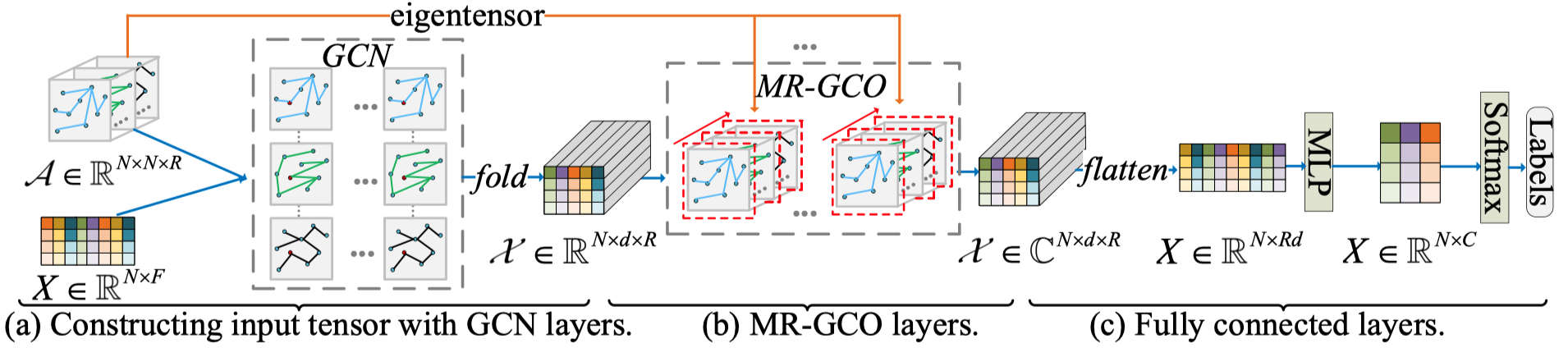
作者在定义了在multi-relational graph中的卷积操作,命名为MR-GCO(multirelational graph convolution operators),提出了一个可以用来做node classification的网络MR-GCN。
motivation:现在的几个解决multi relation的GCN模型,倾向于在不同relation的graph中执行GCN卷积操作,然后混合(blending)结果。作者认为这种做法忽略了relation之间的correlation。
现有的处理multi-relational graph的方法主要有两种思路:
- 每个relation graph下进行GCN,然后融合,比如R-GCN,mGCN,Megan等,在这种情况下relation之间的correlation无法被显式的捕获。
The first line conducts GCN on each single relation and then integrates the results with multi-view learning.
- 另一种思路是把multi-relational graph转换为一个同质图homogeneous graph。比如Multi-GCN等。这一类方法存在的问题是可能存在信息的损失等。
Another line is aggregating the multi-relational graph into a homogeneous graph.
methods:作者在定义了在multi-relational graph中的卷积操作,命名为MR-GCO(multirelational graph convolution operators),提出了一个可以用来做node classification的网络MR-GCN。
contribution:
- 首个通过tensor eigen-decomposition,从GCNs spectral graph theory发展到multi-relational graphs下的convolution operator。
- MR-GCN是通过定义generalized tensor product的tensor eigen-decomposition进行的,因此除了可以基于快速傅里叶变换进行外,还可以融合Haar, Discrete Cosine transform (DCT)等。
MR-GCO是作者论文的核心,主要思想从推导过程来看和一般情况下的图卷积是一致的。
由于对泛化的张量积的核心思想不了解,因此无法确切的理解作者的操作。
MR-GCO的定义,对于图信号 \(x\in \mathbb{R}^{N\times R}\)和过滤器\(g\in \mathbb{R}^{N\times R}\),作者定义为:
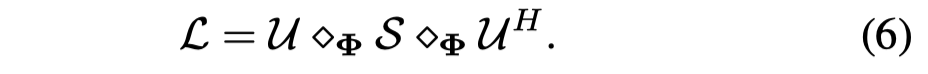
其中\(U\)是对于多关系拉普拉斯矩阵进行张量特征分解后的结果:
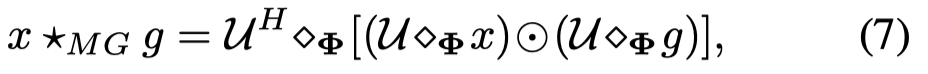
其中的特殊运算 \(\diamondsuit_\Phi\)就是泛化的张量积\(\Phi\)-product,\(\Phi\)是转化矩阵。
其中的拉普拉斯矩阵是多关系的三阶张量,每个relation有一个不同的拉普拉斯矩阵

直接看作者结果