KBGAT
Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs
2019-6-4
将GAT应用到KG上。
1 Introduction
Our architecture is an encoder-decoder model where our generalized graph attention model and ConvKB (Nguyen et al., 2018) play the roles of an encoder and decoder, respectively.
CNN-based和translational-based的模型单独的处理triplet,没有考虑到KG当中某个entity附近的丰富的语义信息。
本论文在GAT的基础上改进。
To the best of our knowledge, we are the first to learn new graph attention based embeddings that specifically target relation prediction on KGs.
3 Our Approach
和之前的GAT模型比较起来,用于知识图谱的话需要考虑relation。
假设每一层的输入包括两个矩阵,entity matrix和relation matrix \[ H\in N_e\times T \\ G\in N_r\times P \] 每一层的输出为: \[ H^{'}\in N_e\times T^{'} \\ G^{'}\in N_r\times P^{'} \]
3.1 Attention
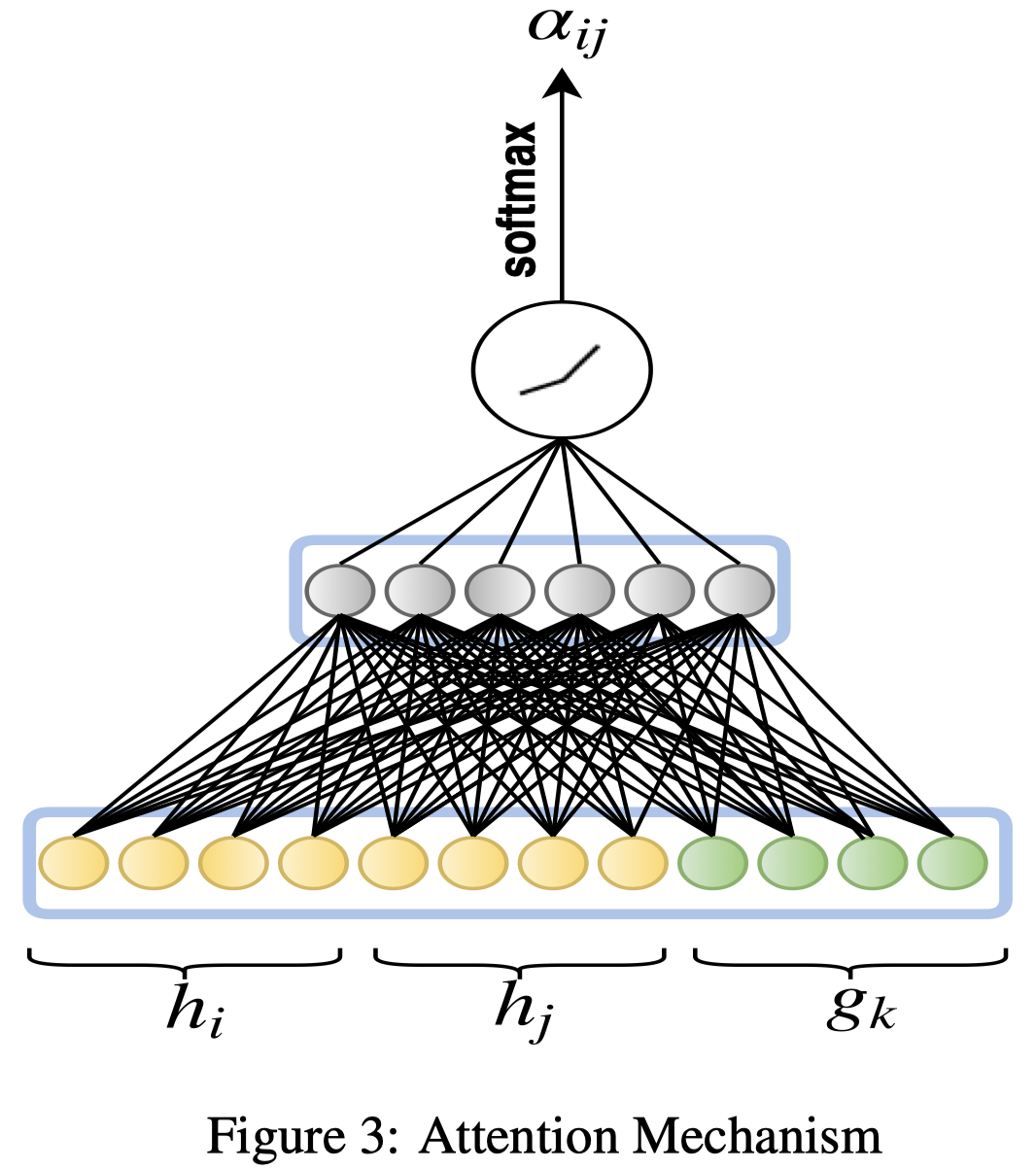
对于一个以\(e_i\)为顶点的edge (i, j, k),应该能够传播给\(e_i\)一个embedding: \[ c_{ijk}=W_1[h_i][h_k][g_j] \] 接下来计算对应的attention value。 \[ b_{ijk}=LeakRelu(W_2c_{ijk}) \\ \alpha_{ijk}=softmax(b_{ijk}) \] 之后进行weighted sum就可以了,neighbour指的是某个的状态 \[ h_i^{'}=\sigma(\sum_{j\in N_i}\sum_{k\in R_{ij}}\alpha_{ijk}c_{ijk}) \]
但类似与GAT中,使用multihead attention机制,在实现的时候作者并不是使用了\(\sigma\),而是使用\(elu\)函数。 \[ h_i^{'}=\lVert_{m=1}^{M} \sigma(\sum_{j\in N_i}\sum_{k\in R_{ij}}\alpha_{ijk}^{m} c_{ijk}^{m}) \] 在这一层传入下一层的时候,作者实现中加了一个dropout层,防止过拟合。
但是在最后一层,就不使用concate操作了, \[ h_i^{'}=\sigma(\frac{1}{M} \sum_{m=1}^M \sum_{j\in N_i} \sum_{k\in R_{ij}} \alpha_{ijk}^{m} c_{ijk}^{m}) \] 最后一层的输出记作\(H^f \in N_e \times T^{f}\)
3.2 对于关系的处理
对于输入的\(G\),前面获得的\(h_i^{'}\)只是针对实体i的,所以关系\(G\)的变换是直接进行线性转换。 \[ G^{'}=GW^R \\ W^R\in R^{P\times P^{'}} \]
3.3 保留原来的entity embedding
在最后一层,加上原来的entity embedding。 \[ H^{''}=W^EH + H^f \]
3.4 Training Objective
hinge-loss: \[ L(\Omega)=\sum_{t_{ij\in S}}\sum_{t_{ij}^{'}\in S^{'}} max(d_{ij}-d_{ij}^{'}+\gamma,\ 0) \]
3.5 Decoder
使用ConVKB作为decoder
4 Experiments and Results
数据集:
- WN18RR (Dettmers et al., 2018),
- FB15k-237 (Toutanova et al., 2015),
- NELL-995 (Xiong et al., 2017),
- Unified Medical Language Systems (UMLS) (Kok and Domingos, 2007)
- Alyawarra Kinship (Lin et al., 2018).