revisting-GCN

发表于 更新于 分类于 ， 阅读次数： 本文字数： 614 阅读时长 ≈ 1 分钟

Revisiting Graph Neural Networks: All We Have is Low-Pass Filters

这篇文章中，作者从图信号处理GSP的角度出发，有三方面的贡献：

  • 首先实验发现大多数的信息隐藏在邻居信息的低频特征中，并且低频特征的信息以及足够丰富；提出了假设1：输入特征包括低频真实特征和噪声。真实特征为机器学习任务提供了足够的信息。
  • 将图信号与传播矩阵相乘对应于低通滤波（low-pass filters），并且提出了gfNN(graph filter neural network)用于分析GCN和SGC
  • 在假设1下，认为SGC、GCN 和 gfNN 的结果与使用真实特征的相应神经网络的结果相似。

作者首先做了一个实验，通过图傅里叶变化，使用不同的频率的信息经过mlp进行预测。

实验结果：

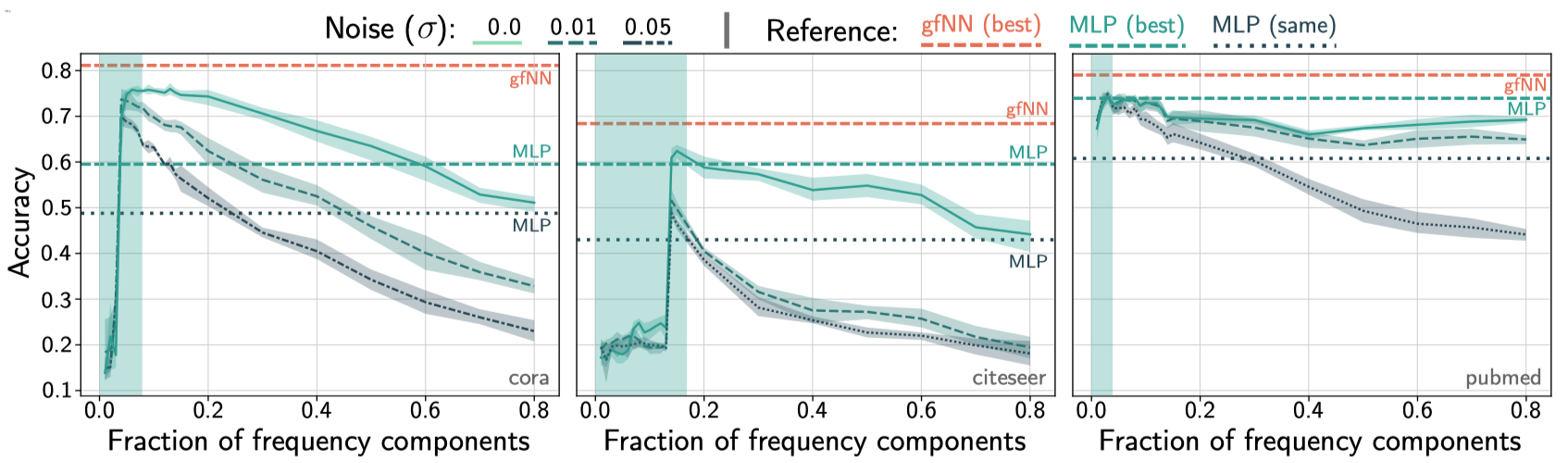
结果分析：高频的邻居信息与中心节点差异较大，可能是噪声；低频的意思是变化不剧烈，中心节点的信号与邻居节点的信号差值不大。虽然人工增加了噪声，但是在低频下没有太多变化。低频特征足以提供足够的信息。

之后，作者证明了将特征矩阵\(X\)与邻居矩阵相乘就是作为低通滤波器。

证明过程来自知乎回答，不是论文本身的内容。

也就是说，与正则化的邻接矩阵相乘时，由于所有的特征都是大于等于0的，因此低频特征对应的\(p(\lambda)\)大，而高频特征对应的\(p(\lambda)\)小，即起到了一个低通滤波的作用。降低高频特征中的噪声，加强低频特征中的信息。