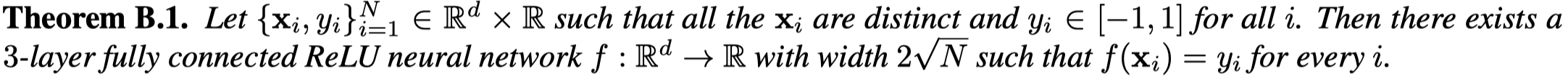GNN-size-generalization

发表于 分类于 ， 阅读次数： 本文字数： 3k 阅读时长 ≈ 3 分钟

From Local Structures to Size Generalization in Graph Neural Networks

ICML 2021

作者主要讨论了GNN对于graph size generalization问题的性质探究。具体一点是指GNN在一个small graph上训练，然后在一个更大的large graph上测试的场景。

主要贡献：

  • 提出了graph的local structure的一种定义，d-pattern。GNN在对于相同的d-pattern会产生相同的输出。因此使用d-pattern可以作为GNN表达能力的一种抽象。
  • 理论上和实验上证明了GNN在size不同的graph上，不能保证学习到的模型是有足够size generalization能力的。
  • 提出了一种基于自监督的方法（Self-Supervised Learning，SSL）来提升size generalization能力，分别有无监督（unsupervised）和半监督（semi-supervised）两种loss设置。训练过程采用了预训练和多任务学习两种不同的学习过程。

Introduction

作者主要的研究场景：small graph训练+large graph测试

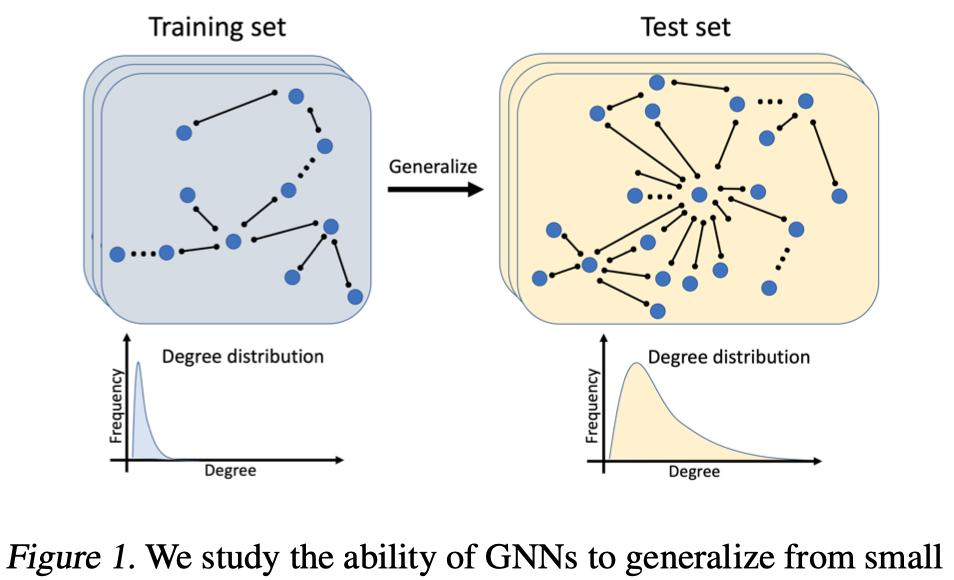
image-20220328201522509

为什么要研究这个问题？作者的出发点：

  1. 理论上，graph的size的差异是很大的，虽然训练好一个graph可以让它在任意size的graph（保证是统一domain下的graph）上运行，但是效果好吗？什么情况下能够做到size泛化？这个问题很有趣（intriguing）但是还没被充分研究。
  2. 实际上，很多large graph想要获得准确的label是很困难的，想要获得large graph的label可能是非常困难的优化问题，也可能对于人来说想要准确的给复杂的graph打label也是很难的。因此，如果GNN能够做到在small graph上训练好，然后很好的泛化到large graph上，就是一个很有意义的研究。

Overview

几个作者希望声明的argument：

  1. 作者提出的d-pattern是研究GNN表达能力的一种合适的抽象表达（d-patterns are a correct notion for studying the expressivity of GNNs.）。依赖于d-pattern，GNN可以输出独立的任意值，对于具有一样d-pattern的node来说，GNN会输出一样的值。因此对于现有的GNN来说，d-pattern直接限制了它的表达能力。

  2. small graph和large graph之间的d-pattern差异，暗示了可能存在某种糟糕的优化选择，导致GNN无法做到size generalization（d-pattern discrepancy implies the existence of bad global minima.）。

  3. GNN在一般的情况下，会倾向于收敛到不泛化的解（GNNs converge to non-generalizing solutions.）。作者进行了实验上的证明，并且也发现，如果尝试不断改变small graph的分布，GNN泛化能力会有相应的提升
  4. GNN的size generalization可以被提升（Size generalization can be improved.）。作者提出了新的SSL的训练方法，可以提升GNN的size generalization能力。

  5. GNN的size泛化，不是简单的L1或L2防止过拟合问题，实际上，如果单纯的加入正则项，反而会让GNN的size generalization能力降低。

GNNs and local graph patterns

来看一下作者定义的d-pattern：

image-20220328203208523

这里的定义与WL-test类似。看看示例图：

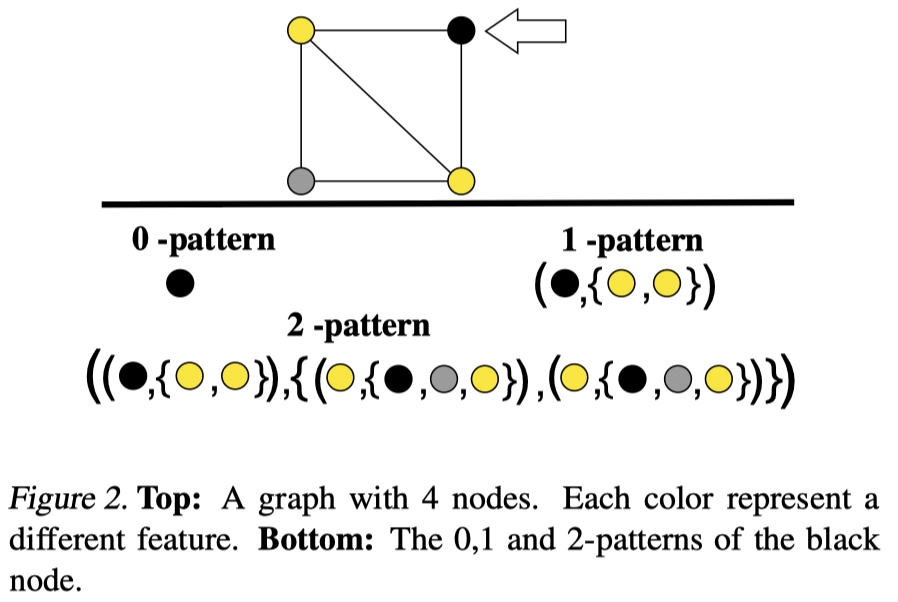
image-20220328203249132

作者提出的两个定理：

  1. 对于具有相同d-pattern的node，任意GNN都会输出相同的值。

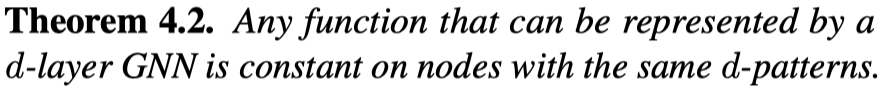
image-20220328203453181

这个定理是说GNN能够表达的映射函数，如果节点的d-pattern一样，那么GNN输出也一样；如果d-pattern不一样，那么GNN输出可能一样，可能不一样。联想到GIN中提出的单射问题，和这个理论是能够联系的。GIN提出的单射问题是希望不同d-pattern能够对于不同的输出。

  1. 对于具有不同d-pattern的node，假设各自不同的d-pattern有不同的label，那么总存在一个GNN能够完美拟合。

image-20220328203635494

”Bad” global minima exist

在这一部分，作者提出GNN可能学习到泛化能力弱的解。

同样，作者提出了两个定理：

  1. 存在一个GNN在small graph上效果很好，但是对于large graph（包含没有在small graph上出现过的d-pattern），可能有任意范围的error。

image-20220328204225483

  1. 一个和上面定理相似的定理，但是描述了small graph和large graph的d-pattern分布差异和可能导致的error。存在一个GNN在small graph上，表现好（指对于d-pattern集合A，\(error<\epsilon\)），但是在large graph上的error更大（指让large graph error最大的集合A的误差）。

image-20220328204906574

Towards improving size generalization

来看一下作者如果尝试解决size generalization问题。首先，作者同时从small graph和large graph上构造了pattern-tree，然后用这个pattern-tree进行学习任务。

pattern-tree：

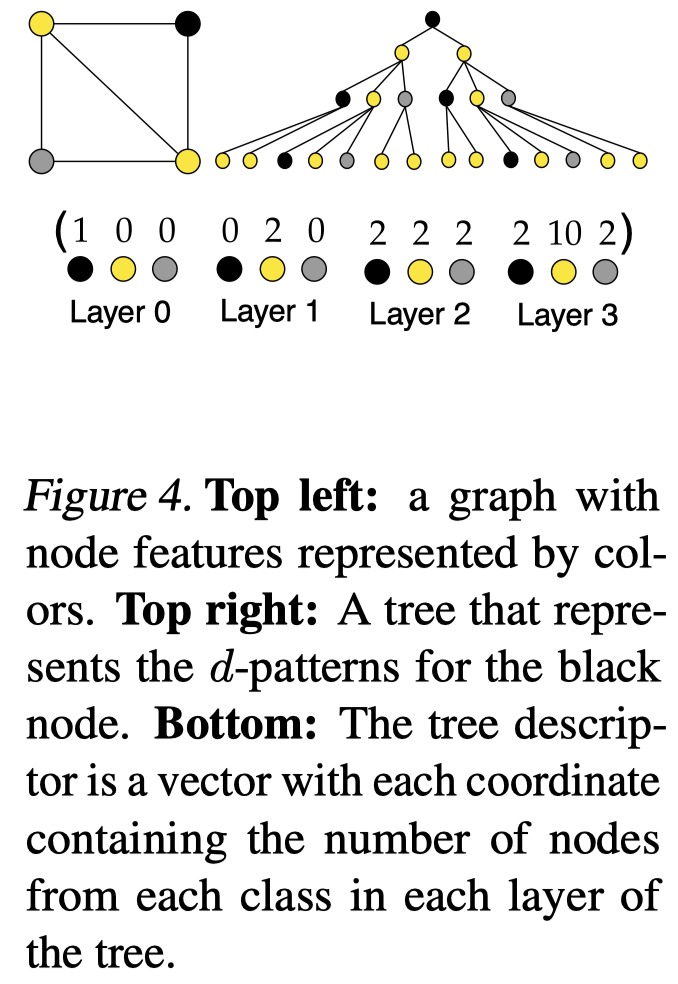
image-20220328205133102

左上角是原来的graph，右上角是node对应的pattern-tree，底部是要预测的值（向量），也就是计算每一层的节点数量。

为什么要使用这个pattern-tree呢？作者在前面发现，GNN的size generalization做不好，就是因为在large graph上会有unseen d-pattern，那么如果提前想办法学习好small和large graph的d-pattern的信息，让两者的d-pattern表示有某种程度的对齐（通过一起训练的方法），是不是就能够提升模型效果？

如果构造pattern-tree：

image-20220328205701565

简单说，就是迭代的往叶子结点上添加它的邻居节点。

怎么使用？

两种训练策略：

  • Pretraining：第一阶段，训练GNN，预测pattern-tree的descriptor；第二阶段，固定GNN值，预测目标task。

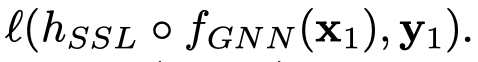
image-20220328210257357

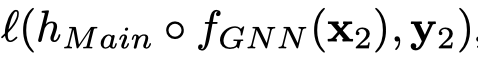
image-20220328210309307

  • Multitask training：同时训练pattern-tree task和main task。

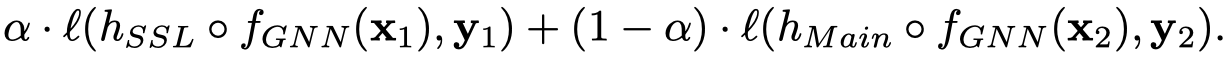
image-20220328210353315

两种设置的示意图：

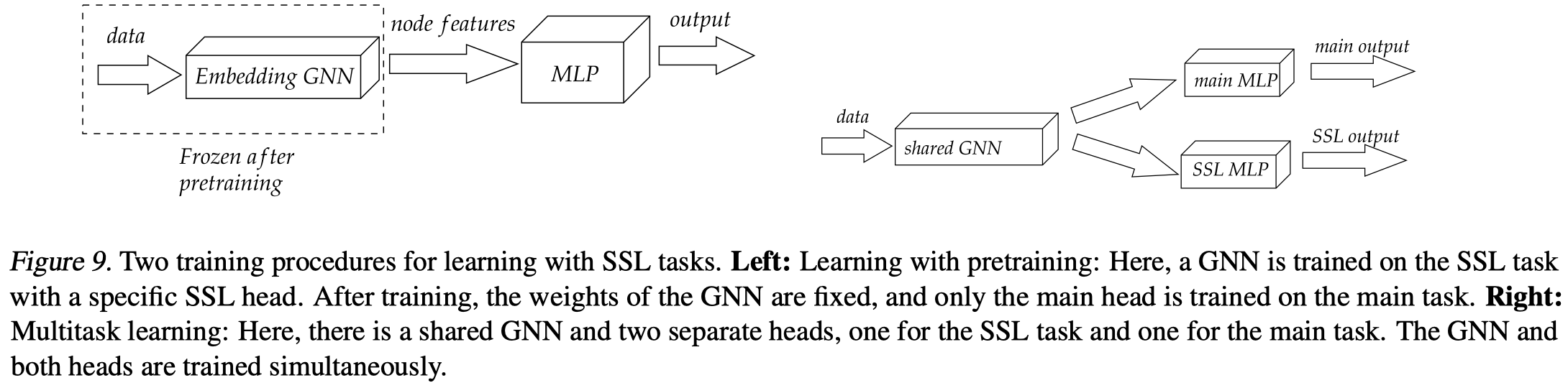
image-20220328210152599

实验发现，还是pretraining的方式更好一点。

作者还尝试了另外的semi-supervised setup，即加入一小部分large graph中有label的data，加入到前面的训练loss中。

Appendix

作者在附录提供了定理详细的证明过程，我只是粗略的看了一遍从直观上认识定理证明是否正确，没有严谨的推导。但是，有一个有意思的前人（Small relu networks are powerful memorizers: a tight analysis of memorization capacity.）提出的定理可以学习：

  • 对于各不相同的输入\(\mathbf{x}_i\)，输出是\(y_i\in[-1,1]\)，总存在一个三层的\(ReLU\)网络可以完美拟合

image-20220328211224061