GCN
SEMI-SUPERVISED CLASSIFICATION WITH G RAPH CONVOLUTIONAL NETWORKS
ICLR 2017
贡献:提出了一种模拟卷积神经网络的变种,直接在图结构上进行类似的卷积操作的神经网络。通过对谱卷积神经网络(Spectral GNN)进行一阶估计简化(first-order approximation),提出了一阶图卷积神经网络——GCN。
1 Introduction
motivation:一般情景下,对图节点进行半监督的分类任务依赖于假设:
connected nodes in the graph are likely to share the same label.
相邻节点倾向于拥有相似的信息,传统的做法是设计基于图的正则项(graph-based regularization)加入到损失函数中,例如下面的图拉普拉斯正则项(a graph Laplacian regularization term)
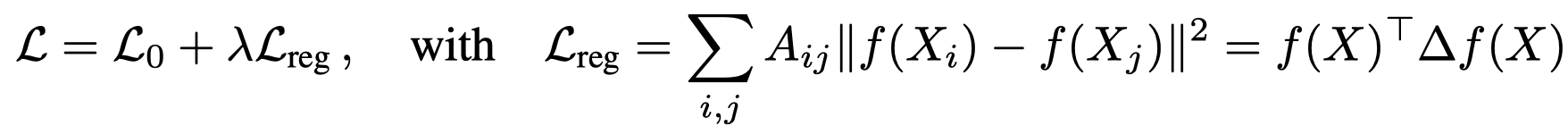
\(L_0\)是有监督的损失,针对graph中有标签的节点;\(L_{reg}\)是图拉普拉斯正则项,它假设邻居拥有与中心节点相似的信息。通过设计上面的损失函数,实际上标签的信息就实现了平滑的传播(label information is smoothed over the graph)。
但是作者认为这种做法可能会限制模型的性能,因为一个graph的edge不一定总是描述节点之间的相似性,它可能包含其它的信息。比如可能是不相似的节点。
method:作者没有继续使用上面的正则化方法,而是直接在graph上建立神经网络,在具体点就是直接基于邻接矩阵或者其它能够描述graph的形式作为输入,输出编码后的信息。
we encode the graph structure directly using a neural network model \(f(X, A)\) and train on a supervised target \(L_0\) for all nodes with labels, thereby avoiding explicit graph-based regularization in the loss function.
这样定义的\(f(X, A)\) 在根据损失\(L_0\)进行梯度计算时,就能够依赖邻接矩阵\(A\)进行梯度的分发(distribute),即实现了对于图结构的学习,无论是有label还是没有label的节点都能够学习到合适的representations。
Conditioning \(f(\cdot)\) on the adjacency matrix of the graph will allow the model to distribute gradient information from the supervised loss \(L_0\) and will enable it to learn representations of nodes both with and without labels.
2 Preliminaries
Graph definition
为了能够利用图结构进行学习,首先我们需要采取某种方式表示图。一个图的常用表达形式是\(G=(V,E)\),\(V\)是节点(vertices)的集合,\(E\)是边(edge)的集合。如果存在边\(e=u,v\),那么\(u\)可以被称作\(v\)的邻居,可以说节点\(u\)和\(v\)是邻接的(adjacent)。
图有几种不同的代数表达形式:
- 邻接矩阵(Adjacency matrix):对于一个简单图\(G=(V,E)\),邻接矩阵\(A\in \mathcal{R}^{n\times n}\)定义为:
\[ A_{ij} = \begin{cases} 1, & \mbox{if }\{ v_i, v_j \}\in E \mbox{ and } i \not= j \\ 0, & \mbox{if }\mbox{ otherwise} \end{cases} \]
- 度矩阵(Degree matrix):度矩阵\(D\in \mathcal{R}^{n\times n}\)是一个对角矩阵s:
\[ D_{ii}=d(v_i) \]
- 拉普拉斯矩阵(Laplacian matrix):拉普拉斯矩阵定义为度矩阵减去邻接矩阵,\(L=D-A\):
\[ L_{ij} = \begin{cases} d(v_i), & \mbox{if } i = j \\ -1, & \mbox{if }\{ v_i, v_j \}\in E \mbox{ and } i\not=j \\ 0, & \mbox{otherwise} \end{cases} \]
- 对称归一化拉普拉斯矩阵(Symmetric normalized Laplacian):将上面的拉普拉斯矩阵归一化: \[ \begin{align} L^{sym}&=D^{-\frac{1}{2}}LD^{-\frac{1}{2}} \\ &=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \end{align} \] 最终得到了归一化拉普拉斯矩阵,矩阵中的元素定义为: \[ L_{ij}^{sym} = \begin{cases} 1, & \mbox{if } i = j \mbox{ and } d(v_i)\not=0 \\ -\frac{1}{\sqrt{d(v_i)d(v_j)}}, & \mbox{if }\{ v_i, v_j \}\in E \mbox{ and } i\not=j \\ 0, & \mbox{otherwise} \end{cases} \]
接下来我们讨论的图是无向图,那么拉普拉斯矩阵是对称矩阵,归一化之后的图拉普拉斯矩阵是半正定对称矩阵。
基于归一化拉普拉斯矩阵,我们可以将它对角化,\(L^{sym}=U\Lambda U^T\),其中\(U=[\mathbf{u}_0,\mathbf{u}_1, \dots,\mathbf{u}_n]\in \mathcal{R}^{n\times n}\)是特征向量矩阵,\(\Lambda_{ii}=\lambda_i\)是特征值。这一对角化实对称矩阵的操作在线性代数中叫做谱分解,\(\Lambda\)称作谱(spectrum)。实对称矩阵的特征向量一定是正交的(orthogonal),特征值一定是实数。特征向量构成了谱空间的基。在图的信号处理中,一个图信号(graph signal)定义为\(x\in \mathcal{R}^n\),每个节点都有一个对应的数值,这一图信号也叫做节点的特征,可以拥有多个特征,那么把多个图信号按列排序就得到了一个图的特征矩阵: \[ X\in \mathcal{R}^{n\times D} \] \(X_i\)表示第\(i\)个节点的特征,\(X_{ij}\)表示第\(i\)个节点的第\(j\)个特征。
在介绍GCN之前,需要介绍首个定义在图上进行的卷积操作原理。
在图信号处理中,模仿一般的傅里叶变换定义了图傅里叶变换(graph Fourier transform),就是将处于原来特征空间下的图信号投影转换到谱空间中, \[ \mathcal{F}(x)=U^Tx \] 傅里叶逆变换定义为: \[ \mathcal{F}^{-1}(x)=U\hat{x} \] 由于图不满足平移不变性,我们希望直接在特征空间下定义图的卷积算子\(f*g\)比较困难,\(x\)是输入的图信号(signal),\(g\)是过滤器(filter)。但利用卷积定理,信号卷积的傅里叶变换等价于信号傅里叶变换的乘积。 \[ \mathcal{F}({x*g})=\mathcal{F}(x)\cdot \mathcal{F}(g) \] 那么图卷积算子可以定义为: \[ {x*g}=\mathcal{F}^{-1}(\mathcal{F}(x)\cdot \mathcal{F}(g)) \] 这样我们无需考虑原特征空间中的卷积,只需要先将信号转换为谱空间中的信号,在谱空间中与谱空间中的过滤器做乘法,最后利用傅里叶逆变换转换到原来的空间中,就实现了图卷积。
更具体的图卷积算子定义为: \[ \begin{align} {x*g}&=\mathcal{F}^{-1}(\mathcal{F}(x)\cdot \mathcal{F}(g)) \\ &=U(U^Tx\cdot U^Tg) \\ \end{align} \] 其中,\(U^Tg\)是一个向量,可以看做是对角矩阵\(g_{\theta}=diag(U^Tg)\),最后谱卷积算子定义为: \[ {x*g}=Ug_{\theta}U^Tx \] 所有基于谱空间的图卷积方法都是在尝试寻找更合适的\(g_{\theta}\)。
FAST APPROXIMATE CONVOLUTIONS ON GRAPHS
Spectral CNN(Spectral Convolutional Neural Network)直接将\(g_{\theta}\)作为一系列可以学习的参数,得到了下面的卷积公式: \[ H^{(l+1)}_{:,j}=\sigma(\sum_{i=1}^{f_{l}} U\Theta^{l}_{i,j}H^{(l)}_{:,i}) \ (j=1,2,3\dots,f_l) \] 这里任然需要计算特征向量,计算代价很大。
之后切比雪夫网络(Chebyshev Spectral CNN,ChebNet)对Spectral CNN进行简化,使用切比雪夫多项式简化\(g_{\theta}\),令\(g_{\theta}=\sum_{i=0}^K\theta_i T_i(\tilde{\Lambda})\),其中\(\tilde{\Lambda}=2\Lambda/\lambda_{max}-I_n\)得到了下面的卷积公式: \[ \begin{align} {x*g} &\approx U\sum_{i=0}^K \theta_i T_i(\tilde{\Lambda}) U^T x \\ &= \sum_{i=0}^K \theta_i T_i(\tilde{L}) x \end{align} \] 其中,\(\tilde{L}=2L/\lambda_{max}-I_n\)。这样ChebNet不需要再计算特性向量\(U^T\)。
3 GCN
GCN在ChebNet的基础上,进一步将K阶多项式限制到了1阶,假设\(\lambda_{max}=2\)得到了新的卷积算子: \[ {x*g} \approx \sum_{i=0}^K \theta_i T_i(\tilde{L}) \approx \theta_0x + \theta_1x(L-I_n)x=\theta_0x + \theta_1 D^{-\frac{1}{2}}AD^{-\frac{1}{2}} x \] 由于半监督图节点分类学习的数据量少,令0阶系数和1阶系数相同,减小学习的参数量。 \[ \begin{align} {x*g} &\approx \theta_0x + \theta_1 D^{-\frac{1}{2}}AD^{-\frac{1}{2}} x \\ &\approx \theta (I_n + D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x \end{align} \] 最终提出了具有多层结构的图卷积神经网络(GCN),每一层使用的卷积函数定义如下: \[ H^{(l+1)}=\sigma (\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}) \] 其中\(\tilde{D}\)和\(\tilde{A}\)是区别于之前的度矩阵和邻接矩阵, \[ \tilde{A}=A+I_N\\ \tilde{D}_{ii}=\sum_j{\tilde{A}_{ij}} \] 原因是在实验中发现,如果使用原来的形式会导致训练的不稳定性以及梯度消失/爆炸的问题,因此重新归一化。
GCN用来做半监督的节点分类任务,在实现的时候使用了两层GCN,最后经过Softmax输出预测值。损失函数使用交叉熵。
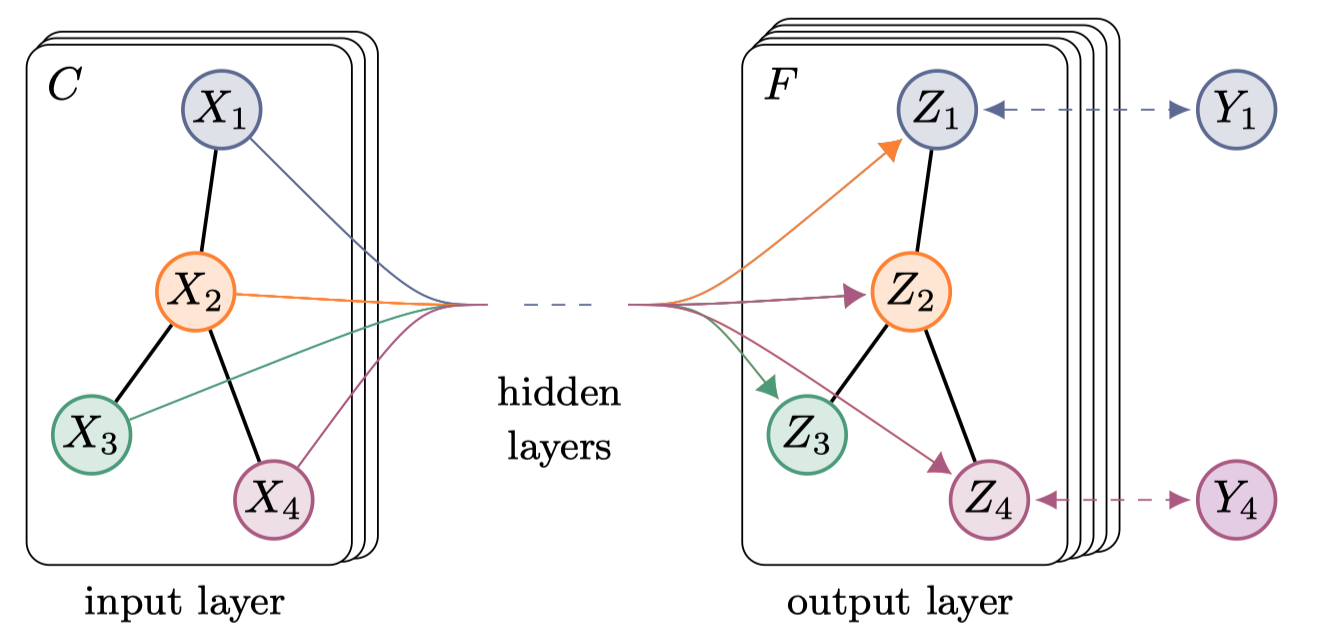
4 EXPERIMENTS
使用以下四方面的实验:
- semi-supervised document classification in citation networks
- semi-supervised entity classification in a bipartite graph extracted from a knowledge graph
- an evaluation of various graph propagation models
- a run-time analysis on random graphs
使用的数据集:

需要注意的一点是对于知识图谱这种有向图,GCN将关系拆出来作为一个联通两个节点的新节点,这样知识图谱就转换为了无向图。
4.1 SEMI-SUPERVISED NODE CLASSIFICATION
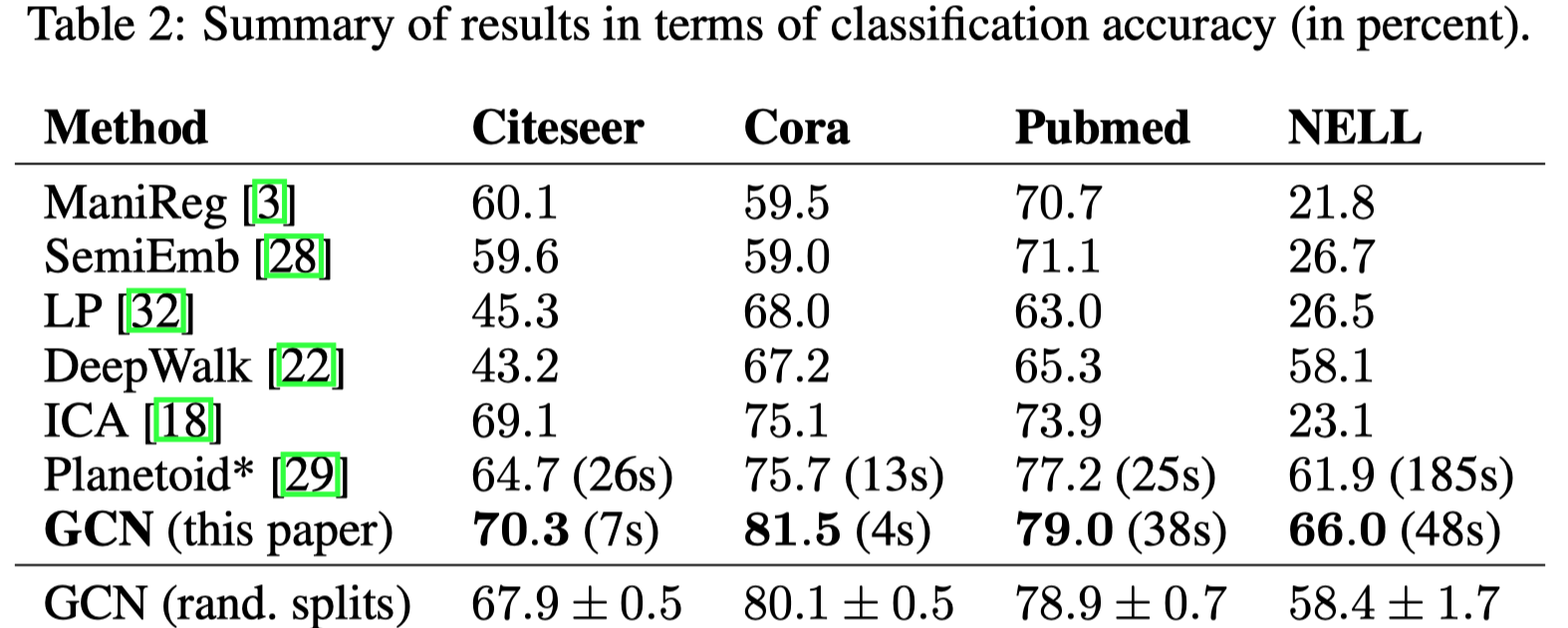
4.2 EVALUATION OF PROPAGATION MODEL
对于GCN机制的一个探究。

4.3 TRAINING TIMEPER EPOCH

5 DISCUSSION
切比雪夫网络是利用切比雪夫多项式对Spectra CNN进行的简化估计,无需再计算特征向量\(U\);GCN是对切比雪夫网络进一步的简化,将K阶多项式限制到了1阶,同时令0阶系数和1阶系数相同,得到了更简洁的图卷积形式。
优点:
- 直接将图卷积算子简化到了一步线性计算的程度
- 形式上来看已经和一般的神经网络非常相似了,方便与已有的深度学习方法进行结合
缺点:
- 内存的限制,需要训练全图
- 无法学习有向图以及边的特征