AM-GCN
AM-GCN: Adaptive Multi-channel Graph Convolutional Networks
2020-8 KDD 2020
AM-GCN主要针对的是节点分类任务,主要贡献包括两点:
- 探究了之前的GCN方法是否能够较好的同时捕获topological structures和node features
- 设计了 a novel adaptive multi-channel GCN framework, 能够适应的同时捕获两种不同的信息
1 Introduction
之前的图卷积神经网络方法使用节点特征(node features)作为初始输入,然后进行图卷积操作。
作者提出的问题:
What information do GCNs really learn and fuse from topological structures and node features?
一般的GNN中涉及到两种信息:
- 拓扑结构(主要指一个节点周围有哪些邻居节点)
- 节点信息(主要指节点本身的特征信息,比如论文节点的标题、关键字等文本信息)
这两个信息都可以用来进行图上的预测任务,但是哪个信息或者两个一起作用,对于最终的预测任务影响比较大?
AM-GCN主要针对的是节点分类任务,主要贡献包括两点:
- 探究了之前的GCN方法是否能够较好的同时捕获topological structures和node features
- 设计了 a novel adaptive multi-channel GCN framework, 能够适应的同时捕获两种不同的信息
2 FUSION CAPABILITY OF GCNS
探究GCN学习结构信息和节点特征信息的能力,设计了两个实验:
Case 1: Random Topology and Correlated Node Features
实验设置:
- 900节点,3 class
- 0.3的概率随机生成边
- 对于3类节点,节点特征使用三个相同协方差,不同均值的高斯分布初始化
- GCN与基于节点特征的MLP对比
结果:GCN分类准确率75.2%,MLP准确率100%
Case 2: Correlated Topology and Random Node Features
实验设置:
- 900节点,3 class
- 设计3 community,community内部建立边的概率是0.03, community内部建立边的概率是0.0015
- 随机生成节点特征
- GCN与Deepwalk(忽略节点特征)
结果:GCN分类准确率87%,MLP准确率100%
3 AM-GCN: THE PROPOSED MODEL
对于一个原始图的输入\(G=(\mathbf{A},\mathbf{X})\),\(\mathbf{A}\)是邻接矩阵,\(\mathbf{X}\)是节点特征矩阵,构造两个图:
- Topology Graph:\(\mathbf{A}_t=\mathbf{A}\),图原始的结构,与GCN一致
- Feature Graph:\(\mathbf{A}_f\),该图中一个节点的相邻节点是k个特征相似的节点,不是原来的结构上的邻居节点
构造Feature Graph,首先计算一个节点与其它所有节点的相似度,计算一个余弦相似度矩阵\(\mathbf{S}\in \mathbb{R}^{n\times n}\) \[ \mathbf{S}_{i,j}=\frac{\mathbf{x}_i\cdot \mathbf{x}_j}{|\mathbf{x}_i| |\mathbf{x}_j|} \] 然后对于节点\(i\),在\(\mathbf{S}\)中选择前\(k\)个相似度最大的节点作为feature node,得到\(\mathbf{A}_f\)。
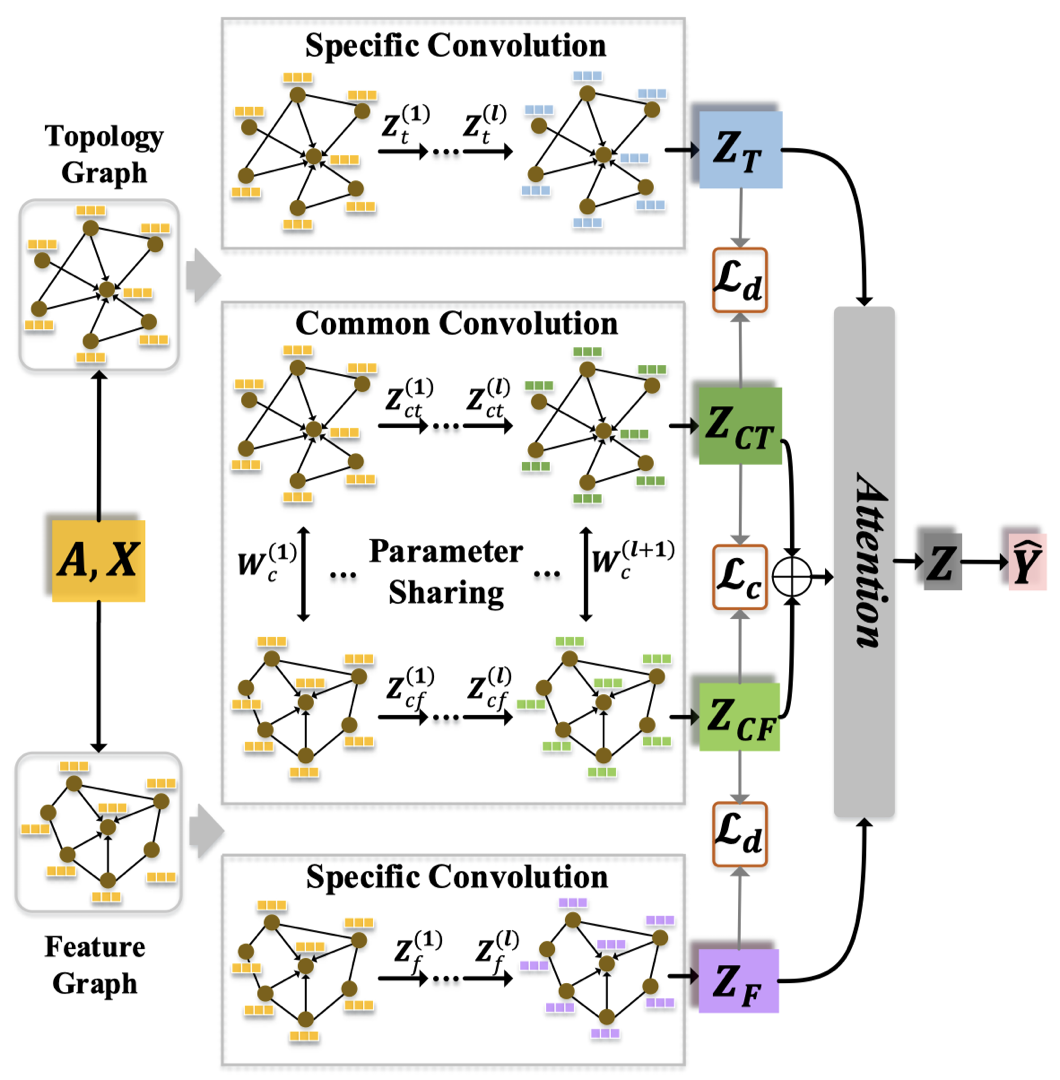
AM-GCN的整体模型图:
可以看到其中有三个主要核心模块,包括在Topology Graph和Feature Graph上的卷积,以及捕获两者共有特征的卷积。
3.1 Specific Convolution Module
在Topology Graph上的卷积: \[ \mathbf{Z}_t^{(l)} = ReLU(\tilde{D}^{-\frac{1}{2}}_t \tilde{A}_t \tilde{D}^{-\frac{1}{2}}_t \mathbf{Z}_t^{(l-1)} \mathbf{W}_t^{(l)} ) \] 其中,\(\tilde{A}_t=A_t+I_t\),该卷积方法与GCN一模一样
在Feature Graph上的卷积: \[ \mathbf{Z}_f^{(l)} = ReLU(\tilde{D}^{-\frac{1}{2}}_f \tilde{A}_f \tilde{D}^{-\frac{1}{2}}_f \mathbf{Z}_f^{(l-1)} \mathbf{W}_f^{(l)} ) \] 其中,\(\tilde{A}_f=A_f+I_f\)
3.2 Common Convolution Module
实际上,feature space和topology space不是完全独立的,两者的信息可能互补然后一起可以用于预测任务。因此,AM-GCN设计了一个common module使用parameter sharing strategy捕获两者的通用特征。
在topology space中导出embedding: \[ \mathbf{Z}_{ct}^{(l)} = ReLU(\tilde{D}^{-\frac{1}{2}}_t \tilde{A}_t \tilde{D}^{-\frac{1}{2}}_t \mathbf{Z}_{ct}^{(l-1)} \mathbf{W}_c^{(l)} ) \] 在feature space中导出embedding: \[ \mathbf{Z}_{cf}^{(l)} = ReLU(\tilde{D}^{-\frac{1}{2}}_f \tilde{A}_f \tilde{D}^{-\frac{1}{2}}_f \mathbf{Z}_{cf}^{(l-1)} \mathbf{W}_c^{(l)} ) \] 最后,两个结合得到common embedding: \[ \mathbf{Z}_{c} = (\mathbf{Z}_{ct} + \mathbf{Z}_{cf})/2 \]
3.3 Two Constraints
Consistency Constraint:
用来控制两个common embedding的consistency,首先将\(\mathbf{Z}_{ct}\)和\(\mathbf{Z}_{cf}\)使用\(l_2\)正则归一化,然后得到下面节点之间的相似度 \[ \mathbf{S}_T=\mathbf{Z}_{CTnor}\cdot \mathbf{Z}_{CTnor}^T \\ \mathbf{S}_F=\mathbf{Z}_{CFnor}\cdot \mathbf{Z}_{CFnor}^T \] 之后约束: \[ \mathcal{L}_c=|| \mathbf{S}_T - \mathbf{S}_F ||^2 \] Disparity Constraint:
因为\(\mathbf{Z}_{ct}^{(l)}\)和\(\mathbf{Z}_{t}^{(l)}\)都是从topology space中学习得到的,为了保证它们都是反映了不同的信息,因此使用Hilbert-Schmidt Independence Criterion (HSIC)加强它们的disparity。 \[ HSIC(\mathbf{\mathbf{Z}_{T}},\ \mathbf{\mathbf{Z}_{CT}}) = (n-1)^{-2}tr(\mathbf{R} \mathbf{K}_T \mathbf{R} \mathbf{K}_{CT}) \] 同样的,对于\(\mathbf{\mathbf{Z}_{F}},\ \mathbf{\mathbf{Z}_{CF}}\): \[ HSIC(\mathbf{\mathbf{Z}_{F}},\ \mathbf{\mathbf{Z}_{CF}}) = (n-1)^{-2}tr(\mathbf{R} \mathbf{K}_F \mathbf{R} \mathbf{K}_{CF}) \] 最终, \[ \mathcal{L}_d =HSIC(\mathbf{\mathbf{Z}_{T}},\ \mathbf{\mathbf{Z}_{CT}}) +HSIC(\mathbf{\mathbf{Z}_{F}},\ \mathbf{\mathbf{Z}_{CF}}) \]
3.4 Attention Mechanism
\[ (\alpha_t, \alpha_c, \alpha_f)=att(\mathbf{Z}_T, \mathbf{Z}_C, \mathbf{Z}_F) \]
以计算\(\alpha_t\)为例: \[ \omega_T = \mathbf{q}^T \cdot tanh(\mathbf{W} \mathbf{z}_T + \mathbf{b}) \\ \alpha_T = softmax(\omega_T) \] 最终AM-GCN得到的节点embedding为: \[ \mathbf{Z} = \mathbf{\alpha}_T \cdot \mathbf{Z}_T + \mathbf{\alpha}_C \cdot \mathbf{Z}_C + \mathbf{\alpha}_F \cdot \mathbf{Z}_F \]
4 EXPERIMENTS
4.1 Node Classification
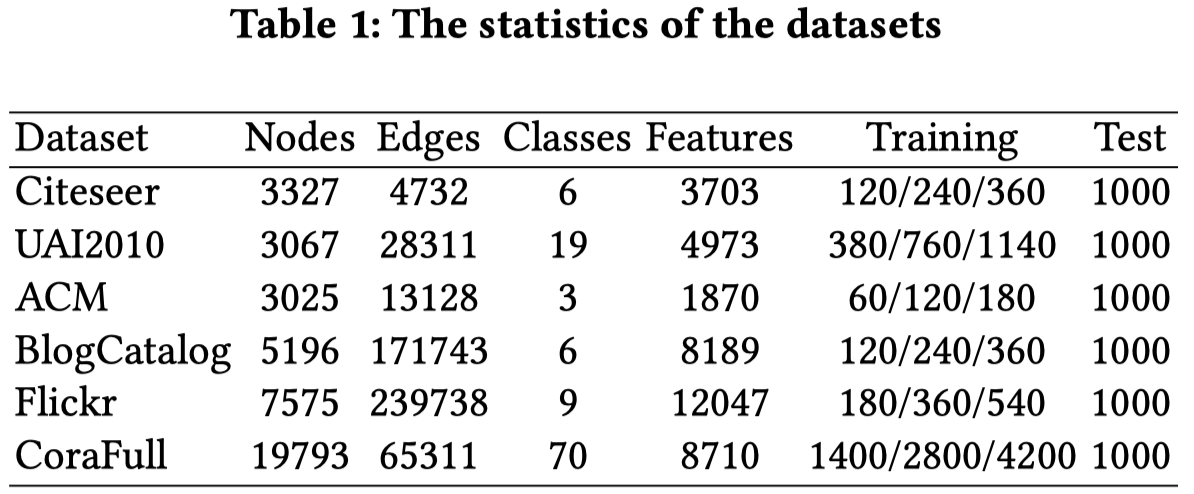
在7个数据集上进行评估,数据集主要是论文的引文网络和社交网络
注意其中的每个数据集训练集有三个级别,分别对应每一类的节点有标签的比例为20%, 40%和60%,测试集恒定每一类由1000个节点评估。
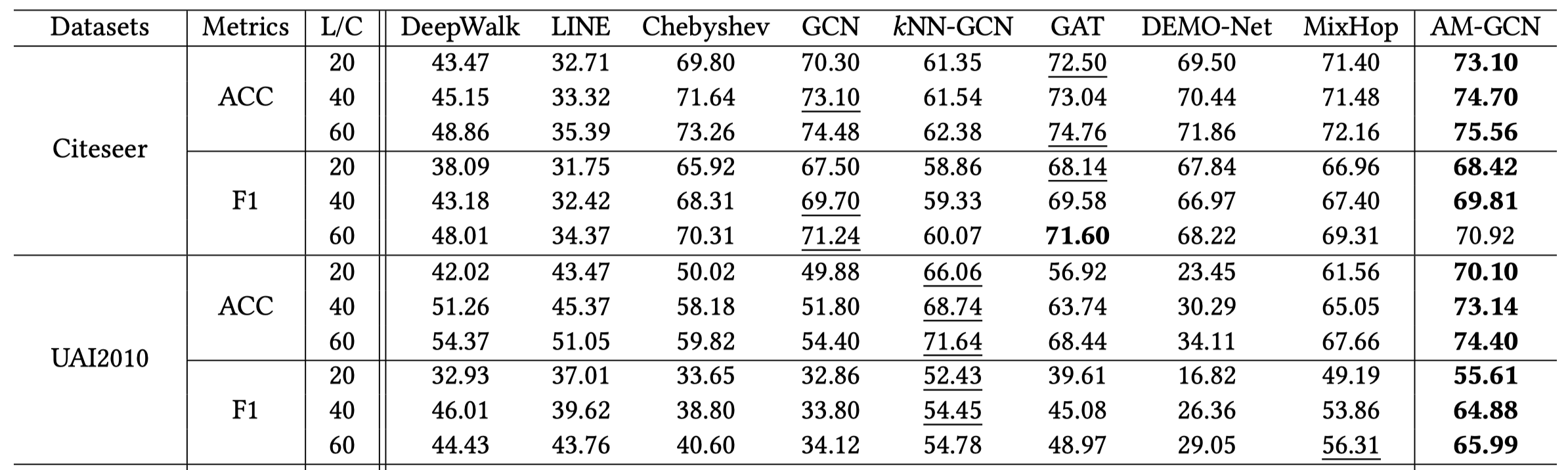
其中,kNN-GCN是AM-GCN只在feature graph上进行聚合。
对比GCN和kNN-GCN一个比较有意思的结果是不聚合邻居,有时候根据特征聚合相似的节点,也可能取得更好的结果。
4.2 Analysis of Variants
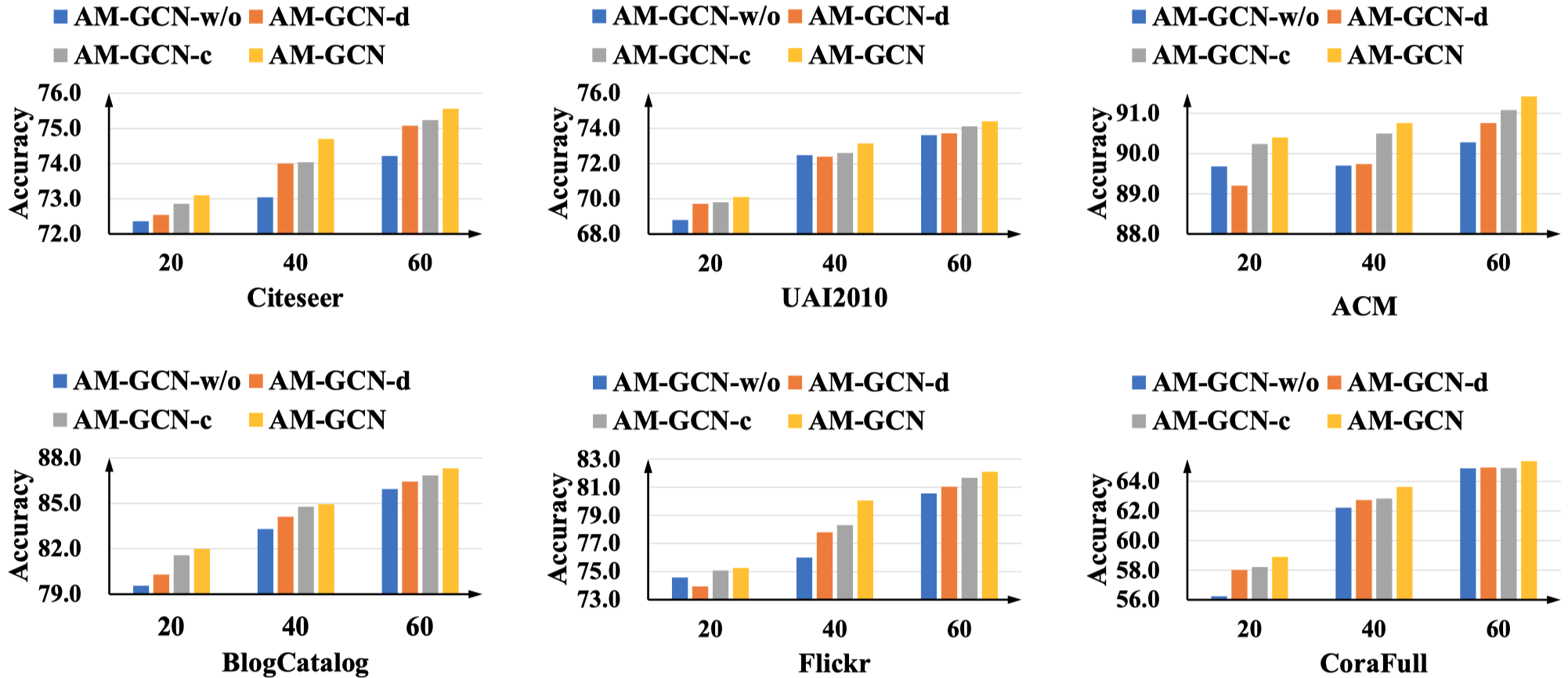
比较设计的约束的作用:
AM-GCN-w/o: AM-GCN without constraints \(L_c\) and \(L_d\)
AM-GCN-c: AM-GCN with the consistency constraint \(L_c\)
AM-GCN-d: AM-GCN with the disparity constraint \(L_d\)
可以看出来,一般情况下,consistency constraint比disparity constraint更加重要
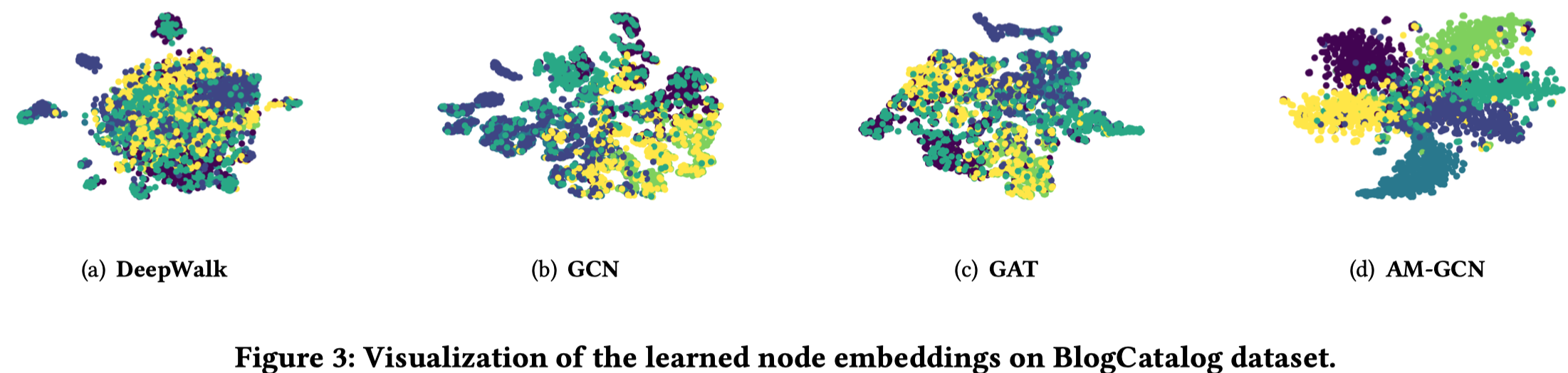
4.3 Visualization
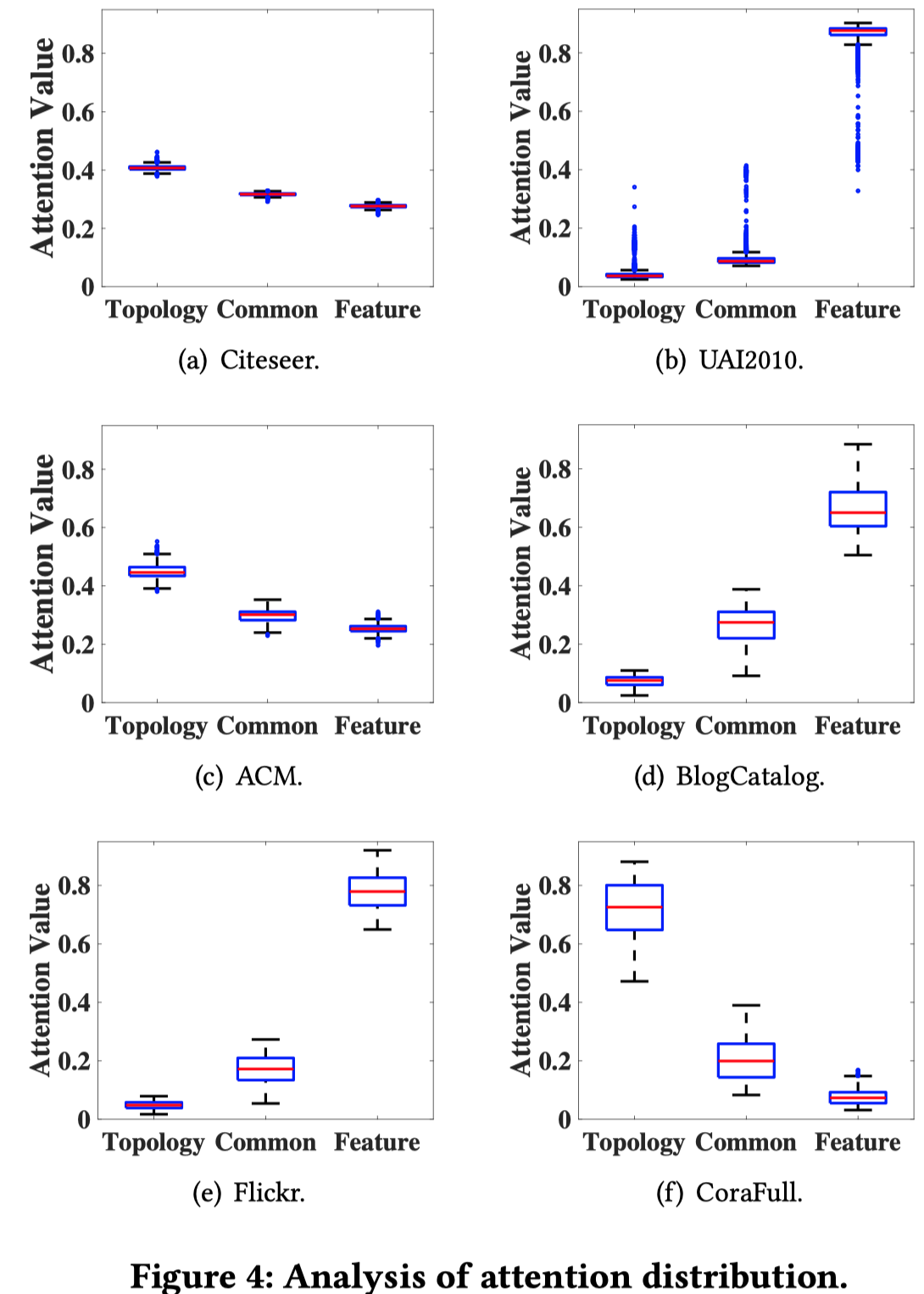
4.4 Analysis of Attention Mechanism
分析不同数据集下,三个不同embedding的注意力值的分布
可以看到,不同数据集下,三个不同方面的embedding对应的注意力值不同,说明哪个方面包含了更加丰富的信息是依赖于具体数据的。