PoE-MoE

Product-of-Experts and Mixture-of-Experts

这篇博客主要记录PoE和MoE的一些调研笔记。

Products of Experts

Hinton 1999年 ICANN

It is possible to combine multiple probabilistic models of the same data by multiplying the probabilities together and then renormalizing. This is a very efficient way to model high-dimensional data which simultaneously satisfies many different low dimensional constraints. Each individual expert model can focus on giving high probability to data vectors that satisfy just one of the constraints. Data vectors that satisfy this one constraint but violate other constraints will be ruled out by their low probability under the other expert models. Training a product of models appears difficult because, in addition to maximizing the probabilities that the individual models assign to the observed data, it is necessary to make the models disagree on unobserved regions of the data space. However, if the individual models are tractable there is a fairly efficient way to train a product of models. This training algorithm suggests a biologically plausible way of learning neural population codes.

PoE实际就是一种融合多个不同分布的方法，大致上可以理解为一种分布求和（&）的操作，具体公式为：

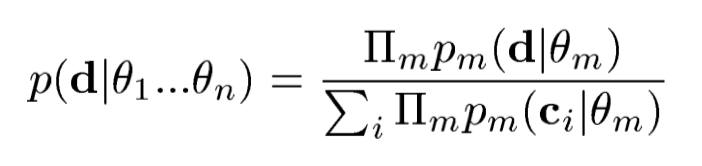
其中，\(\mathbf{d}\)是指一个特定的vector，\(\theta_m\)是指第\(m\)个expert network的参数。上面的公式实质就是多个分布相乘，然后重新归一化。在这篇原始论文中，expert可以理解为一个弱一点的互不相同的model，比如在识别手写数字的任务中，有的expert可以用来识别数字的整体形状，有的expert可以用来关注更小的patch细节。通过融合多个experts，就可能获得一个更加强大的model。

上述公式对\(\theta_m\)进行求导：

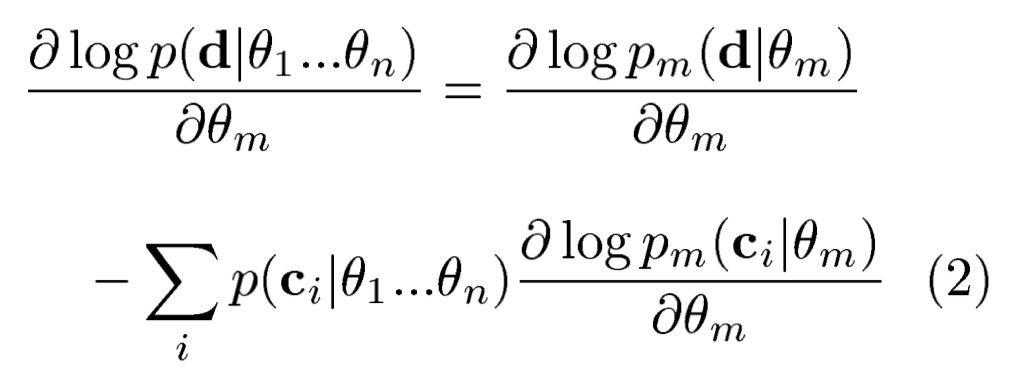
Generalized Product-of-Experts for Learning Multimodal Representations in Noisy Environments

ICMI 2022，一个拓展PoE并且应用到multimodal VAE上的工作。核心是通过动态评估每个模态预测隐藏state \(z\)的weight，然后多个模态预测结果相乘：

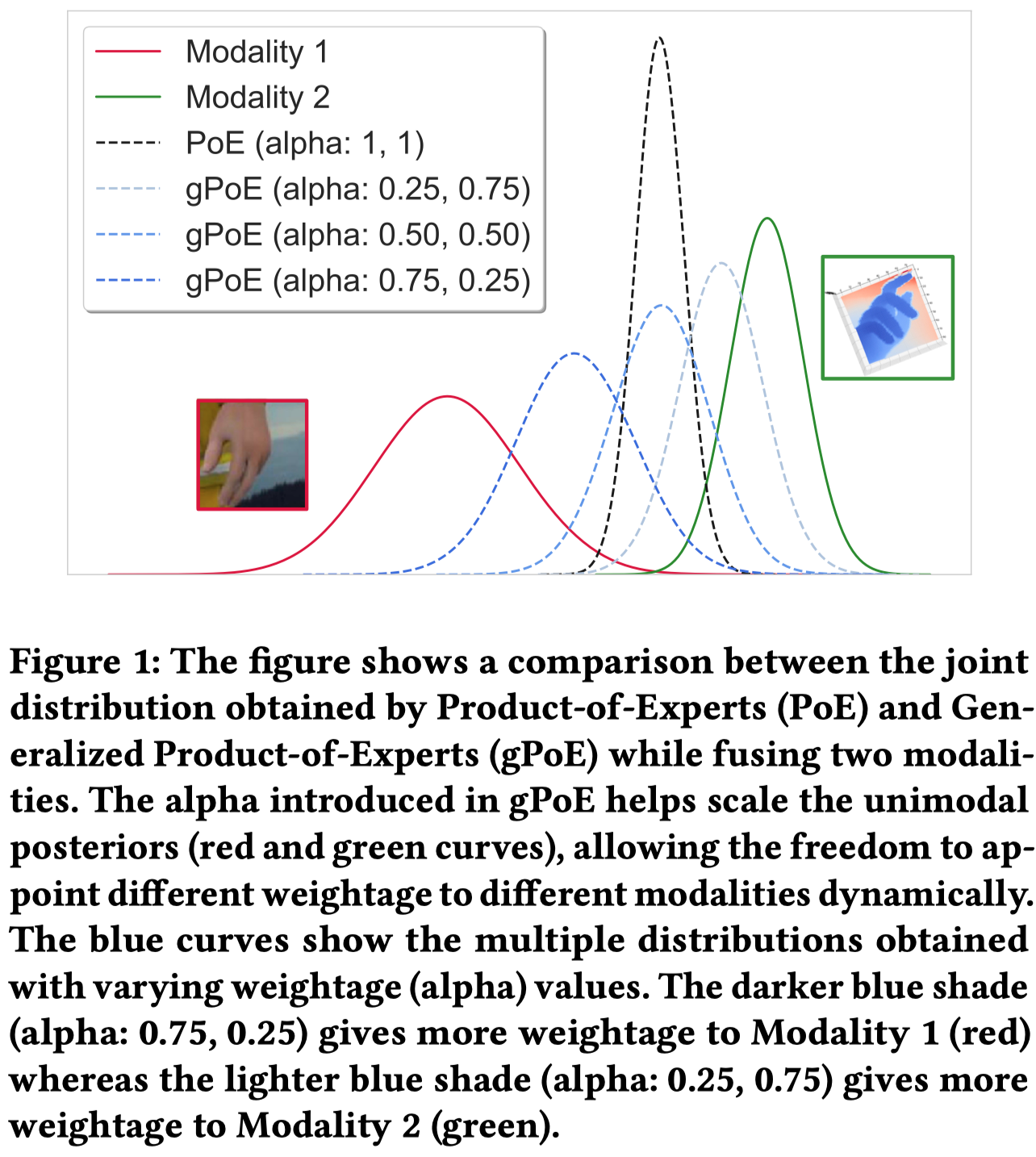
模型图：

不同模态编码的隐藏状态\(z_i\)的同一维度的weight和是1。

个人感觉这个方法和MoE的最大区别就是使用了相乘操作，而不是相加。

Adaptive Mixtures of Local Experts

MoE，混合专家系统（mixture of experts），1991年，Neural Computation

We present a new supervised learning procedure for systems composed of many separate networks, each of which learns to handle a subset of the complete set of training cases. The new procedure can be viewed either as a modular version of a multilayer supervised network, or as an associative version of competitive learning. It therefore provides a new link between these two apparently different approaches. We demonstrate that the learning procedure divides up a vowel discrimination task into appropriate subtasks, each of which can be solved by a very simple expert network.

这篇论文比较早，它提出混合专家系统的出发点是，如果说使用单个网络来执行多个不同的小的子任务，这些子任务之间的互相干扰可能使得学习过程变慢，泛化性也变差。

当然，上面这个观点也不总是成立的，随着网络越来越强大，很多之前认为会互相干扰的任务现在不再互相干扰了，反而能互相促进。当然从另一方面讲，这种任务会互相干扰，需要拆分的思想到现在也是随处可见的，只不过是人们对于在哪一个level的任务需要拆分的认识发生了变化。

那么，很自然的思路是，如果我们可以提前把数据集进行划分，让不同的model去学习对应的不同的数据bias，最后融合到一起是不是效果能更好，训练更简单？这种尝试学习不同bias的model被称作“expert”。

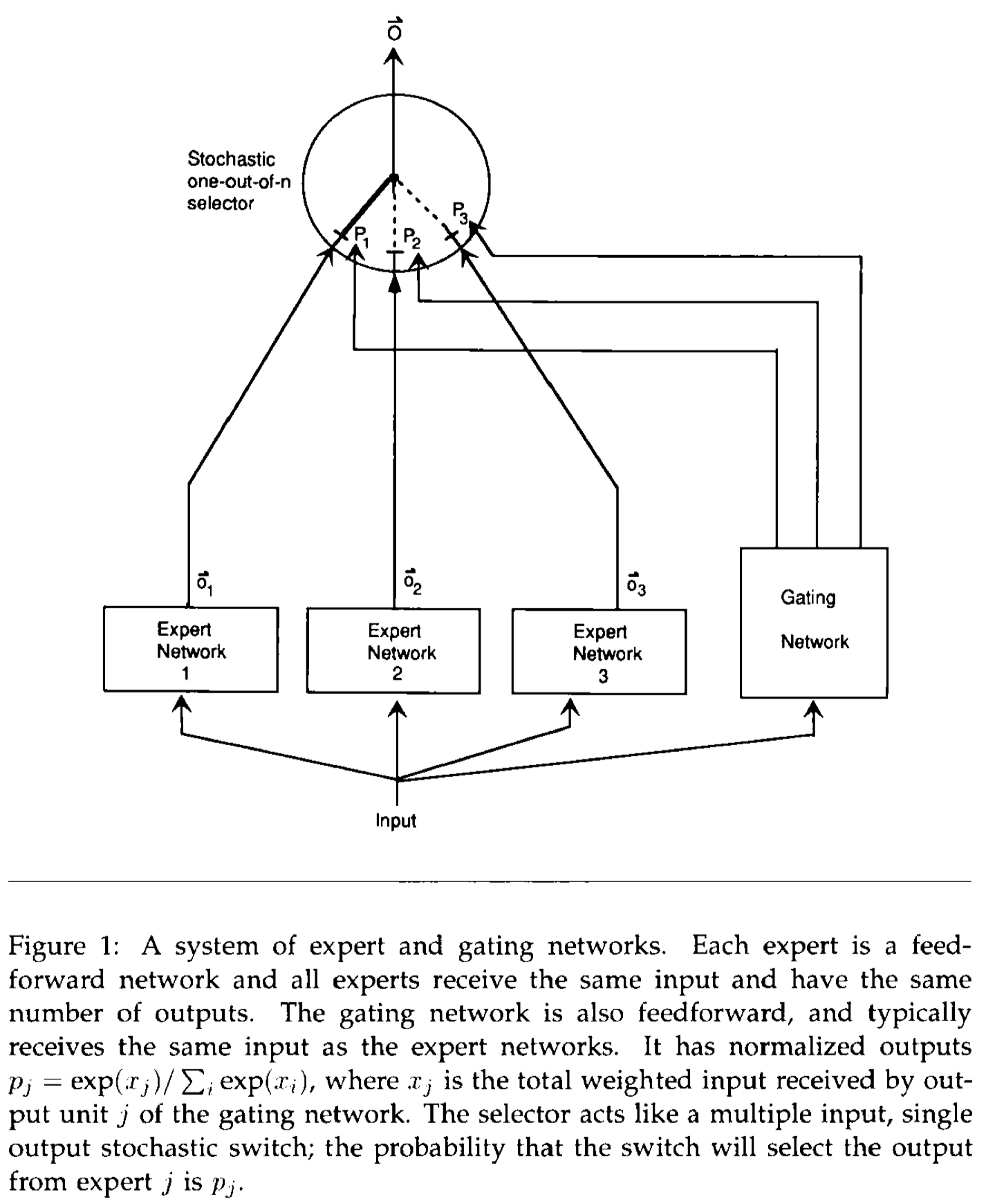
之前研究者提出过混合expert思路，那就是使用gating network来控制不同expert的权重：

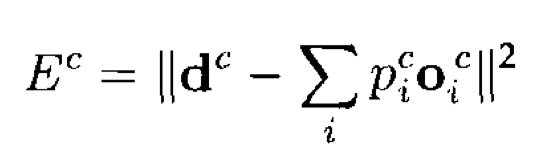
\(\mathbf{d}\)是目标vector，\(p_i\)是第\(i\)个expert的权重，\(o\)是第\(i\)个expert的输出。

仔细看一下这个公式，它直接融合多个expert的输出拿到一个总的输出，然后计算这个总的输出和\(\mathbf{d}\)之间的差距。它实际上鼓励每个expert去减小其它expert残留的error，这样的耦合程度比较重。如果一个expert发生了改变，那么其它所有的expert也需要发生相应的改变。

上面的做法是鼓励不同expert互相协作。那这篇论文中作者提出不要互相协作，而是互相竞争，每次只选择一个expert进行预测。仅仅通过简单的改变loss function就能够达到这一目的：

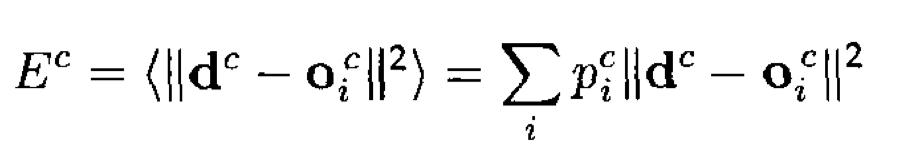
这一个改变的核心是，让每一个expert都单独去靠近\(\mathbf{d}\)，因此，不同expert是相对独立的优化和\(\mathbf{d}\)之间的差距，而不需要优化其它expert的residual error。

试想下，在这种情况中，如果某个expert的error更小，那么它的权重\(p_i\)会被优化得更大；如果某个expert的error更大，那么它的权重\(p_i\)会被优化得更小。也就是互相竞争，哪个expert表现更好，模型会直接倾向于完全使用这个expert来解决问题，而不是总需要所有的expert参与。

下面是核心的思路图：

在实际中，作者使用了另一种改进版，能够更快速更好的进行梯度优化：

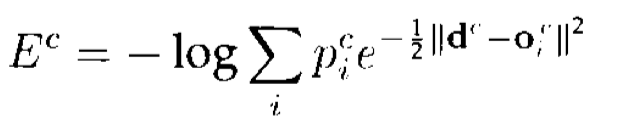
梯度的改变：

下面的解释是Hinton的CSC321课件上的说明，感觉更清晰。

如果输入和输出之间存在不同的映射关系，那么用把输入划分到不同的分区，然后让不同的模型来预测可能更合适。

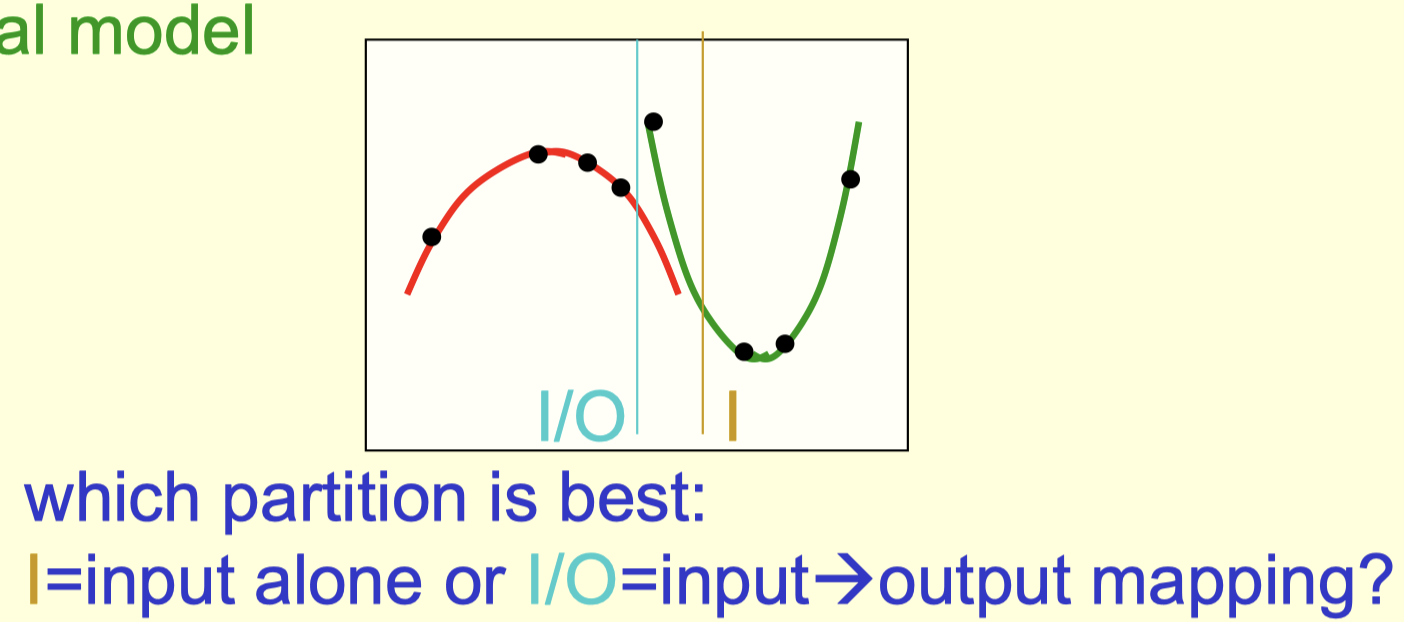
这样子做的核心思想是让expert集中在表现比其它expert都要好的特定情况下。

The key idea is to make each expert focus on predicting the right answer for the cases where it is already doing better than the other experts.

但是如果我们直接平均的混合多个预测器，可能使得expert被用来缓解其它expert的残留错误：

在上图中，为了让\(expert_i\)弥补其它\(expert\)的错误error，会导致\(expert_i\)的预测\(y_i\)反而远离真正的目标\(d\)。

因此，作者鼓励不同的expert互相竞争而不是互相合作（如同上文提到的）：

从另一角度，最小化平方误差可以等价的看做是最大化正确答案的log概率：

MoE可以看做是决策树，每个expert看做是叶子节点，通过gating network将输入划分到不同的expert节点上：

A mixture of experts can be viewed as a probabilistic way of viewing a decision stump so that the tests and leaf functions can be learned by maximum likelihood.

Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer

ICLR 2017，Google brain

The capacity of a neural network to absorb information is limited by its number of parameters. Conditional computation, where parts of the network are active on a per-example basis, has been proposed in theory as a way of dramatically increasing model capacity without a proportional increase in computation. In practice, however, there are significant algorithmic and performance challenges. In this work, we address these challenges and finally realize the promise of conditional computation, achieving greater than 1000x improvements in model capacity with only minor losses in computational efficiency on modern GPU clusters. We introduce a Sparsely-Gated Mixture-of-Experts layer (MoE), consisting of up to thousands of feed-forward sub-networks. A trainable gating network determines a sparse combination of these experts to use for each example. We apply the MoE to the tasks of language modeling and machine translation, where model capacity is critical for absorbing the vast quantities of knowledge available in the training corpora. We present model architectures in which a MoE with up to 137 billion parameters is applied convolutionally between stacked LSTM layers. On large language modeling and machine translation benchmarks, these models achieve significantly better results than state-of-the-art at lower computational cost.

这篇论文提出了稀疏的MoE方法，使得基于RNN架构的模型参数量也可以以达到上千亿的规模，从而在机器翻译这些需要处理大量数据的任务上取得了较好的效果。

模型结构：

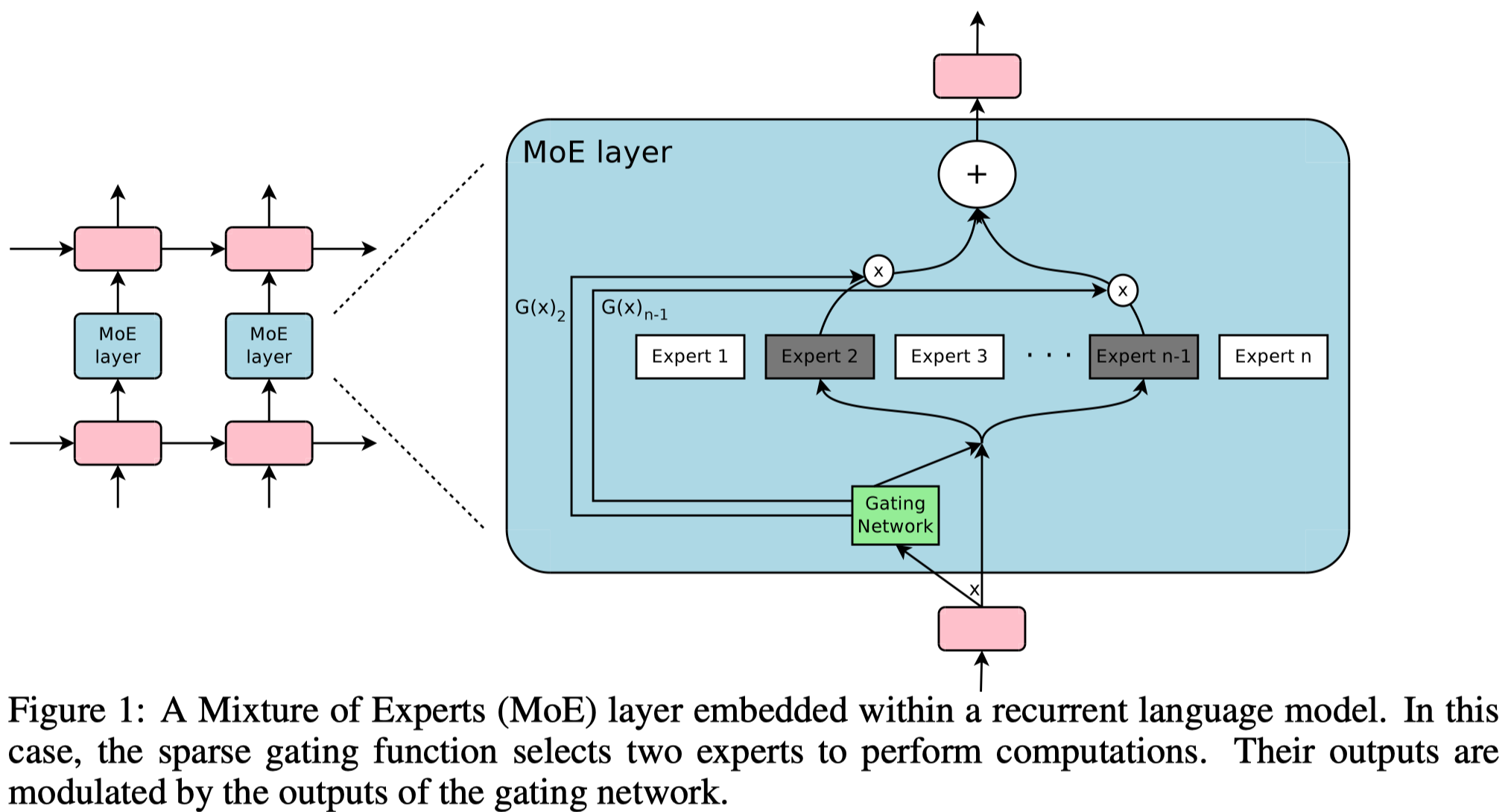
核心在于MoE，作者使用了上千个expert network，每个expert network是\(512\times 1024\)+\(ReLU\)+\(1024\times 512\)+\(sigmoid\)总计\(1M\)参数量的FFN。最后所有的expert输出相加（这里更像是前面MoE论文中作者改进前的融合形式）：

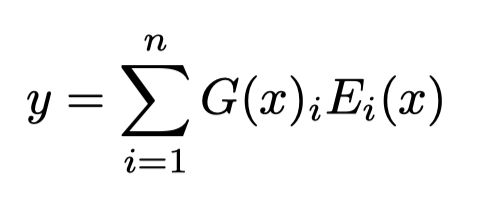
\(G_i(x)\)是权重，\(E_i(x)\)是第\(i\)个expert的输出。

这么多的expert如果都需要参加计算的话计算负担太大，因此作者提出了Sparsely-Gated MoE。

稀疏是通过只选择少数的\(K\)个expert参与最后的输出，在论文中\(K\)取值在\(2-4\)：

为了让所有的expert都能够在总体样本范围内起作用，加入了高斯noise。其中的\(Softplus=log(1+e^x)\)激活函数可以看做是ReLU函数的平滑。

最后，为了避免总是只有少数的expert会起作用，作者加入了额外的loss，希望每个expert在一个batch样本范围内，都能够起作用：

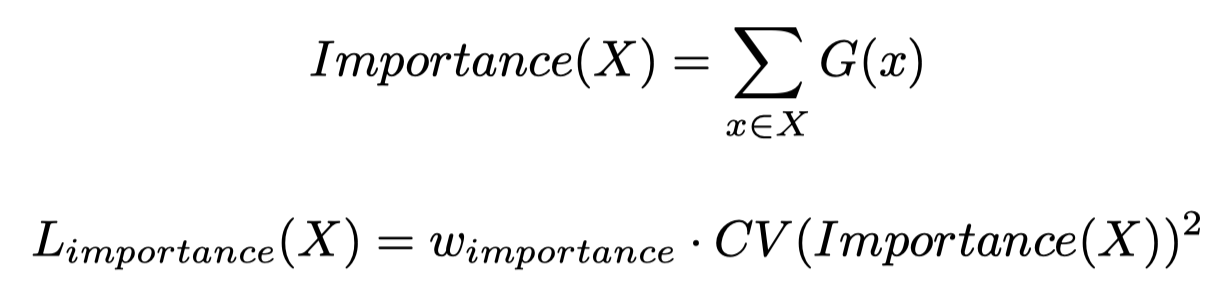
\(X\)是指一个batch的所有样本，\(w_{importance}\)是人工超参，\(CV\)是指coefficient of variation变异系数。\(CV=标准差/均值\)，用来衡量数据的离散/变异程度，消除了量纲的影响。

上述公式的实质是减小不同expert在一个batch内权重和的偏差程度。

Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts

谷歌公司，KDD 2018

Neural-based multi-task learning has been successfully used in many real-world large-scale applications such as recommendation systems. For example, in movie recommendations, beyond providing users movies which they tend to purchase and watch, the system might also optimize for users liking the movies afterwards. With multi-task learning, we aim to build a single model that learns these multiple goals and tasks simultaneously. However, the prediction quality of commonly used multi-task models is often sensitive to the relationships between tasks. It is therefore important to study the modeling tradeoffs between task-specific objectives and inter-task relationships.

In this work, we propose a novel multi-task learning approach, Multi-gate Mixture-of-Experts (MMoE), which explicitly learns to model task relationships from data. We adapt the Mixture-ofExperts (MoE) structure to multi-task learning by sharing the expert submodels across all tasks, while also having a gating network trained to optimize each task. To validate our approach on data with dierent levels of task relatedness, we rst apply it to a synthetic dataset where we control the task relatedness. We show that the proposed approach performs better than baseline methods when the tasks are less related. We also show that the MMoE structure results in an additional trainability benet, depending on different levels of randomness in the training data and model initialization. Furthermore, we demonstrate the performance improvements by MMoE on real tasks including a binary classification benchmark, and a large-scale content recommendation system at Google.

将MoE应用到多任务学习上的工作，提出了MMoE方法，在推荐任务上进行了验证：

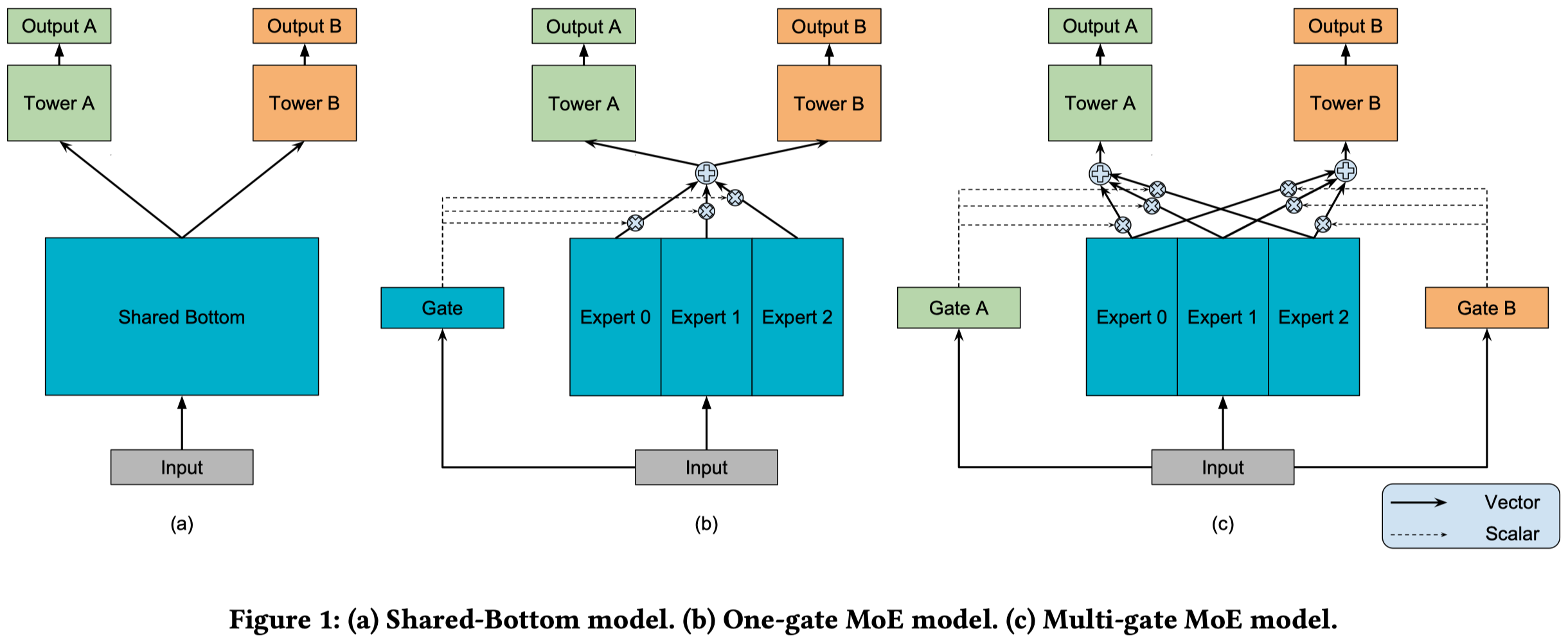
最大的改进点有两个：

• 不同task之间的底层共享网络使用\(n\)个expert网络代替
• 每个task有独立的gating network，这样就让每个task可以自由选择底层共享的网络结构部分

核心数学公式：

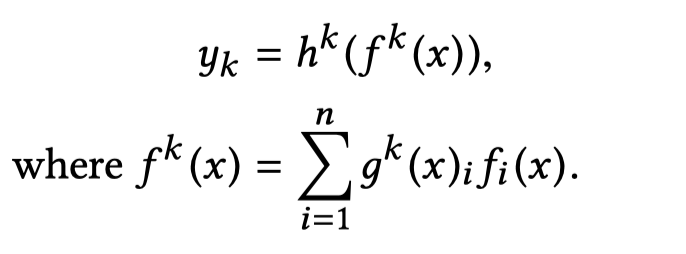
其中\(h^k\)代表task \(k\)的上层tower network，\(f^k\)是MMoE选择的experts，\(g^k\)是task \(k\)的gating network，\(f_i\)是第\(i\)个expert网络。

如果两个task关联性比较大，那么它们选择的experts会重叠的比较多；如果关联性较弱，那么选择experts重叠的就比较少。

GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding

谷歌公司，ICLR 2021

Neural network scaling has been critical for improving the model quality in many real-world machine learning applications with vast amounts of training data and compute. Although this trend of scaling is affirmed to be a sure-fire approach for better model quality, there are challenges on the path such as the computation cost, ease of programming, and efficient implementation on parallel devices. In this paper we demonstrate conditional computation as a remedy to the above mentioned impediments, and demonstrate its efficacy and utility. We make extensive use of GShard, a module composed of a set of lightweight annotation APIs and an extension to the XLA compiler to enable large scale models with up to trillions of parameters. GShard and conditional computation enable us to scale up multilingual neural machine translation Transformer model with Sparsely-Gated Mixture-ofExperts. We demonstrate that such a giant model with 600 billion parameters can efficiently be trained on 2048 TPU v3 cores in 4 days to achieve far superior quality for translation from 100 languages to English compared to the prior art.

首个将MoE应用到Transformer的模型，使用MoE来构建了一个用于机器翻译6千亿参数量的Transformer模型，同时保证计算效率。

MoE在Transformer中的几点设计：

• MoE是设计在FFN层，每隔一个Transformer block，替换FFN为MoE
• MoE是稀疏的，只选择top-2的experts
• 每个expert network是个两层MLP
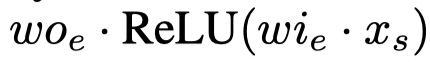
• gating network是个简单的softmax
• 为了让expert负载均衡，每个expert都能够充分训练，给每个expert设计了容量上限，如果某个输入token选择的expert超过了容量上限，这个expert不会处理输入的token
• 加入了一个辅助的loss来进一步平衡expert负载
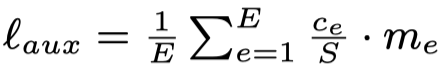
• 对于选择的第2重要expert，如果它的weight过于低可能没有太大必要让它继续处理，因此作者直接让top-2 expert依据weight大小随机决定是否要让top-2 expert网络处理。

Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity

谷歌公司，JMLR 2022

In deep learning, models typically reuse the same parameters for all inputs. Mixture of Experts (MoE) models defy this and instead select different parameters for each incoming example. The result is a sparsely-activated model—with an outrageous number of parameters—but a constant computational cost. However, despite several notable successes of MoE, widespread adoption has been hindered by complexity, communication costs, and training instability. We address these with the introduction of the Switch Transformer. We simplify the MoE routing algorithm and design intuitive improved models with reduced communication and computational costs. Our proposed training techniques mitigate the instabilities, and we show large sparse models may be trained, for the first time, with lower precision (bfloat16) formats. We design models based off T5-Base and T5-Large (Raffel et al., 2019) to obtain up to 7x increases in pre-training speed with the same computational resources. These improvements extend into multilingual settings where we measure gains over the mT5-Base version across all 101 languages. Finally, we advance the current scale of language models by pre-training up to trillion parameter models on the “Colossal Clean Crawled Corpus”, and achieve a 4x speedup over the T5-XXL model.

作者通过简化MoE实现了在保持computing efficiency的情况下增大模型参数量，最终实现了上万亿参数量的模型。

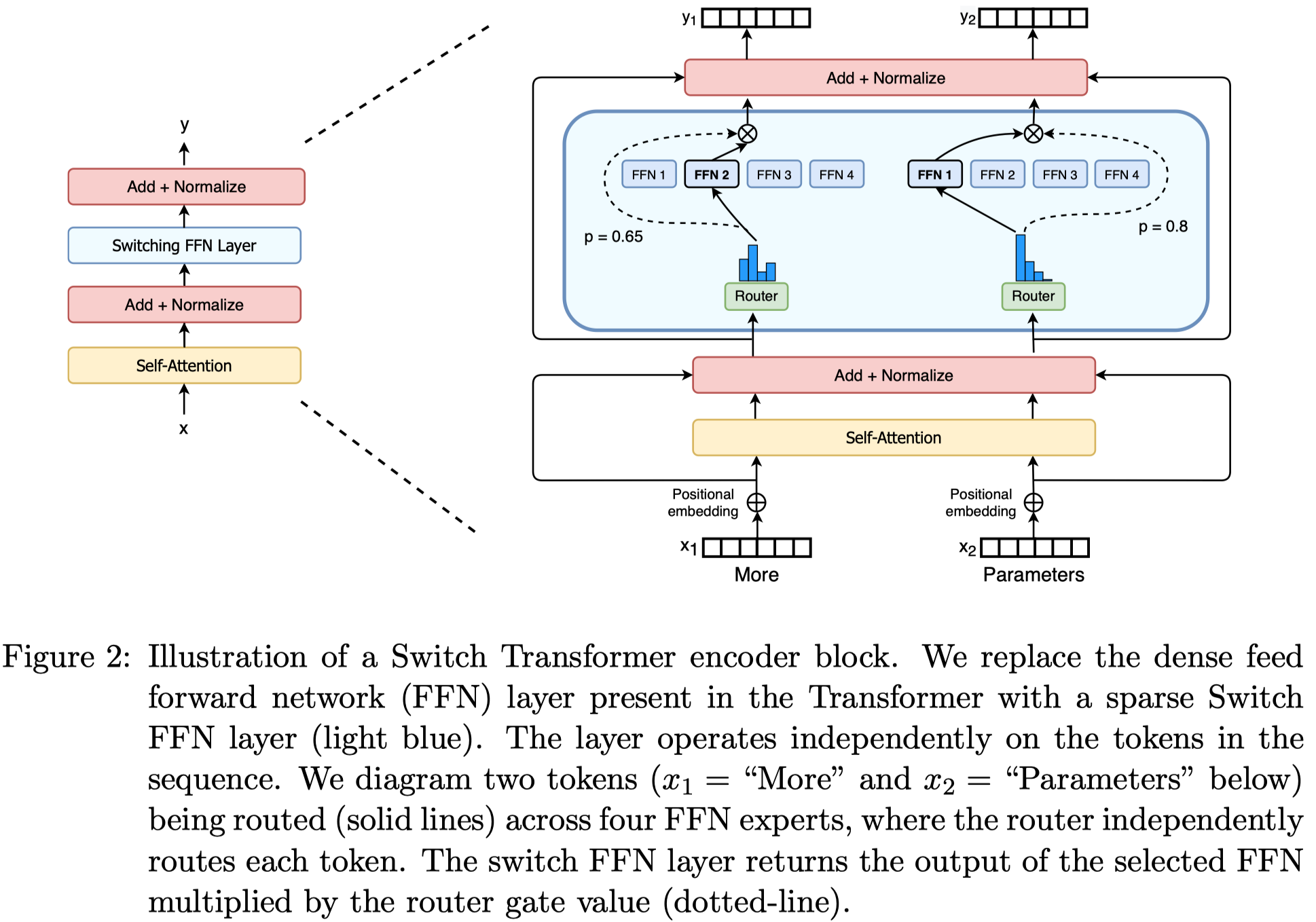
这里最大的简化就是仅仅激活top-1的expert。作者把只选择1个expert的做法称为switch，类比了电路开关，一个开关只能够有一个触点让一个灯泡亮。

另一个有趣的设计是考虑expert负载均衡，通过加入一个loss：

上面这个auxiliary loss在每个\(f_i\)也就是分配给expert \(i\)的token数量不变的情况下，会尝试让\(p_i\)减小，那么也会逐渐的让\(f_i\)变小，最终让所有expert分配的\(f_i\)比较均匀。

Multimodal Contrastive Learning with LIMoE: the Language-Image Mixture of Experts

谷歌大脑，NeurIPS 2022，使用MoE构建的大规模多模态预训练模型LIMoE。

Large sparsely-activated models have obtained excellent performance in multiple domains. However, such models are typically trained on a single modality at a time. We present the Language-Image MoE, LIMoE, a sparse mixture of experts model capable of multimodal learning. LIMoE accepts both images and text simultaneously, while being trained using a contrastive loss. MoEs are a natural fit for a multimodal backbone, since expert layers can learn an appropriate partitioning of modalities. However, new challenges arise; in particular, training stability and balanced expert utilization, for which we propose an entropy-based regularization scheme. Across multiple scales, we demonstrate remarkable performance improvement over dense models of equivalent computational cost. LIMoE-L/16 trained comparably to CLIP-L/14 achieves 78.6% zero-shot ImageNet accuracy (vs. 76.2%), and when further scaled to H/14 (with additional data) it achieves 84.1%, comparable to state-of-the-art methods which use larger custom per-modality backbones and pre-training schemes. We analyse the quantitative and qualitative behavior of LIMoE, and demonstrate phenomena such as differing treatment of the modalities and the organic emergence of modality-specific experts.

下图是LIMoE的结构，单纯从结构图上还不能看出有什么大的特点：

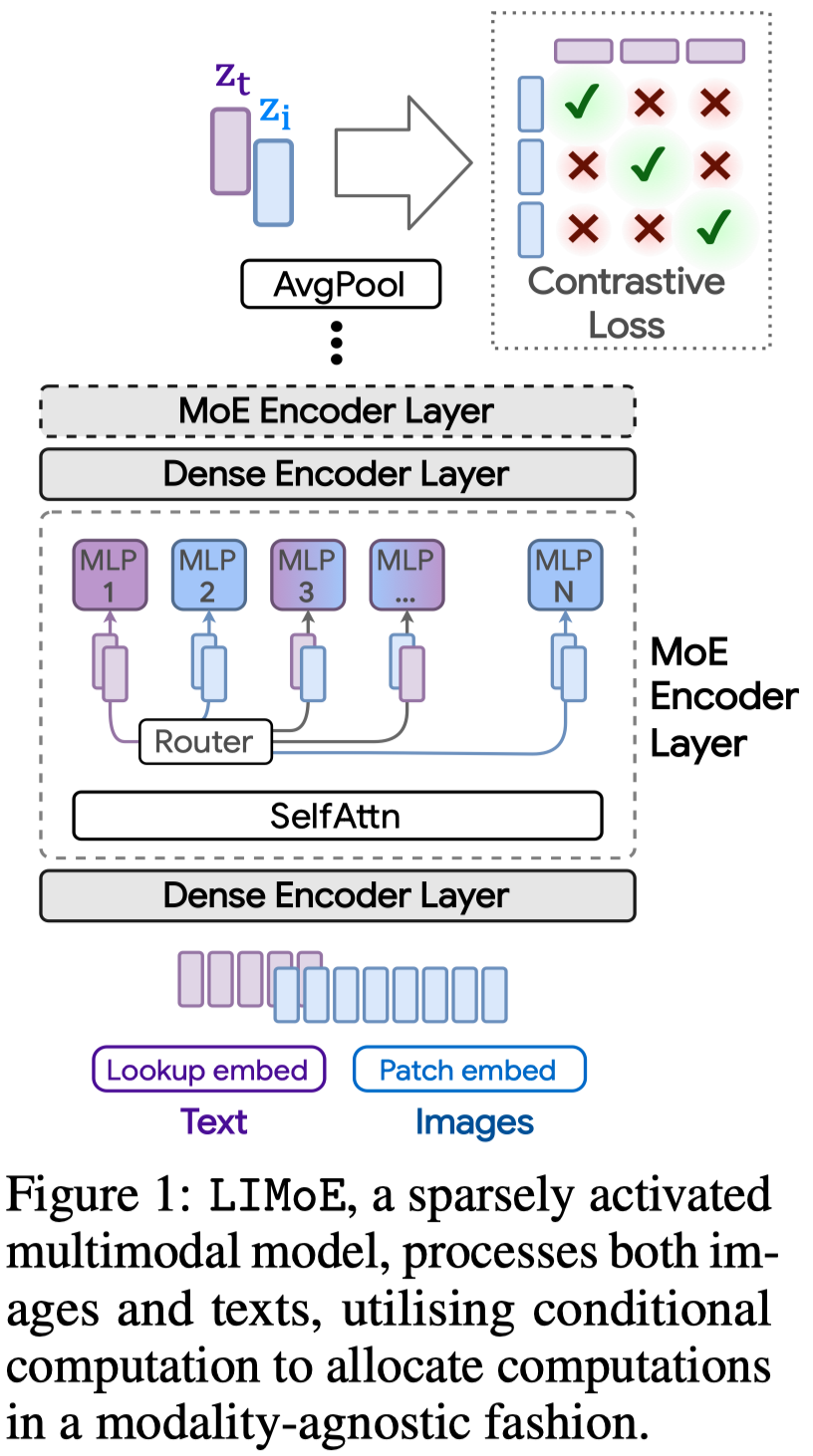
LIMoE使用了单塔Transformer同时处理图像和文本，使用对比学习对齐image-language pair：

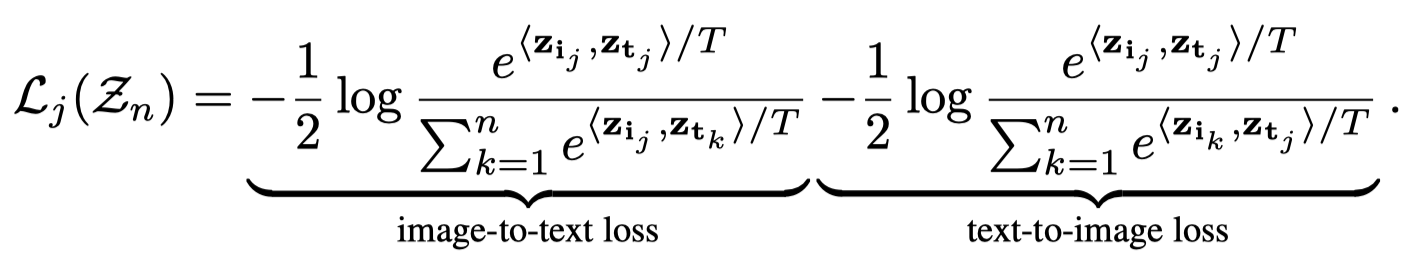
LIMoE除了使用一般的expert负载均衡loss外，还额外考虑了当MoE应用到多模态时遇到的新问题。由于不同模态的数据量不平衡，数据量少的模态可能无法均匀分配到不同expert上，但是从整体上来看experts仍然是负载均衡的。

因此LIMoE对于单个模态\(m\)引入了额外的两个loss：

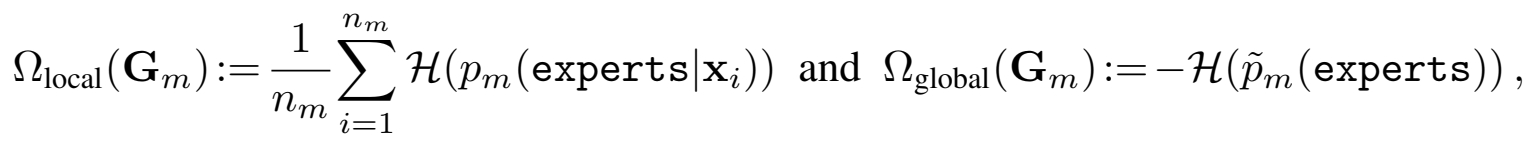
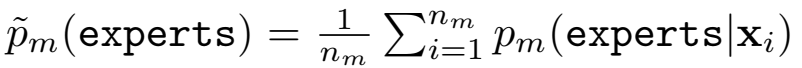
其中\(\mathcal{H}\)表示熵，\(x_i\)是模态\(m\)输入的一个token。local loss是每个token对应的expert概率熵的平均，global loss是每个expert在所有输入token范围内的总体概率熵的平均的负值。

local loss迫使每个token对应的expert概率预测分布更加集中；

global loss迫使expert在输入范围内分布更加分散；

Using Mixture of Expert Models to Gain Insights into Semantic Segmentation

CVPR 2020

MoE应用在CV领域的一篇论文，通过将图片划分为不同的子集，然后让两个expert分别去处理，让expert学习不同的映射关系，最后集成两个expert网络的预测输出：

expert网络的CNN架构一样，中间的gating network接收的是expert网络第42层的feature map输出。作者使用MoE，然后对比expert 1、2和MoE融合的预测label，尝试给一些可解释理由。

MoE与PoE对比

PoE的一个坏处是会让某个过分confident的expert起作用，比如一个expert的概率预测过于低，会导致最后整个融合的概率也低，相比较之下，MoE就更加温和：

When employing PoE, each expert holds the power of veto—in the sense that the joint distribution will have low density for a given set of observations if just one of the marginal posteriors has low density.

By contrast, MoE does not suffer from potentially overconfident experts, since it effectively takes a vote amongst the experts, and spreads its density over all the individual experts.

Variational Mixture-of-Experts Autoencoders for Multi-Modal Deep Generative Models NeurIPS 19