LLM-reason
使用LLM的推理方法
使用LLM进行推理的相关论文总结
CoT
Chain-of-Thought Prompting Elicits Reasoning in Large Language Models
Google Research,NeurIPS 2022
We explore how generating a chain of thought—a series of intermediate reasoning steps—significantly improves the ability of large language models to perform complex reasoning. In particular, we show how such reasoning abilities emerge naturally in sufficiently large language models via a simple method called chain-of-thought prompting, where a few chain of thought demonstrations are provided as exemplars in prompting.
Experiments on three large language models show that chain-of-thought prompting improves performance on a range of arithmetic, commonsense, and symbolic reasoning tasks. The empirical gains can be striking. For instance, prompting a PaLM 540B with just eight chain-of-thought exemplars achieves state-of-the-art accuracy on the GSM8K benchmark of math word problems, surpassing even finetuned GPT-3 with a verifier.
首次提出了chain-of-thought思路的论文。简单说就是在上下文学习中,对于每个输出输出样例examplar,加入中间的推理步骤,格式为<input, chain of thought, output>:
A chain of thought is a series of intermediate natural language reasoning steps that lead to the final output, and we refer to this approach as chain-of-thought prompting.
CoT灵感的来源是两个:
- First, techniques for arithmetic reasoning can benefit from generating natural language rationales that lead to the final answer. 之前的rationale-augmented training的方法发现通过利用自然语言描述的中间步骤rationales可以帮助解决数学推理问题;但是这种方法需要获得大量的rationales,实际上是很难获得的。
- Second, large language models offer the exciting prospect of in-context few-shot learning via prompting. LLM已经通过上下文学习模拟样例,可以解决很多问题,无需训练。但是在需要推理能力的任务上表现很差
作者CoT的思想就是融合了这两种思路,如果能够获得中间推理的步骤,可以帮助解决推理问题;而上下文学习又能够让LLM模拟少数几个样例,无训练的快速学习;那么如果让LLM学会模拟几个样例中的推理步骤,是不是就可以让LLM也迅速学会模拟推理?
方法:
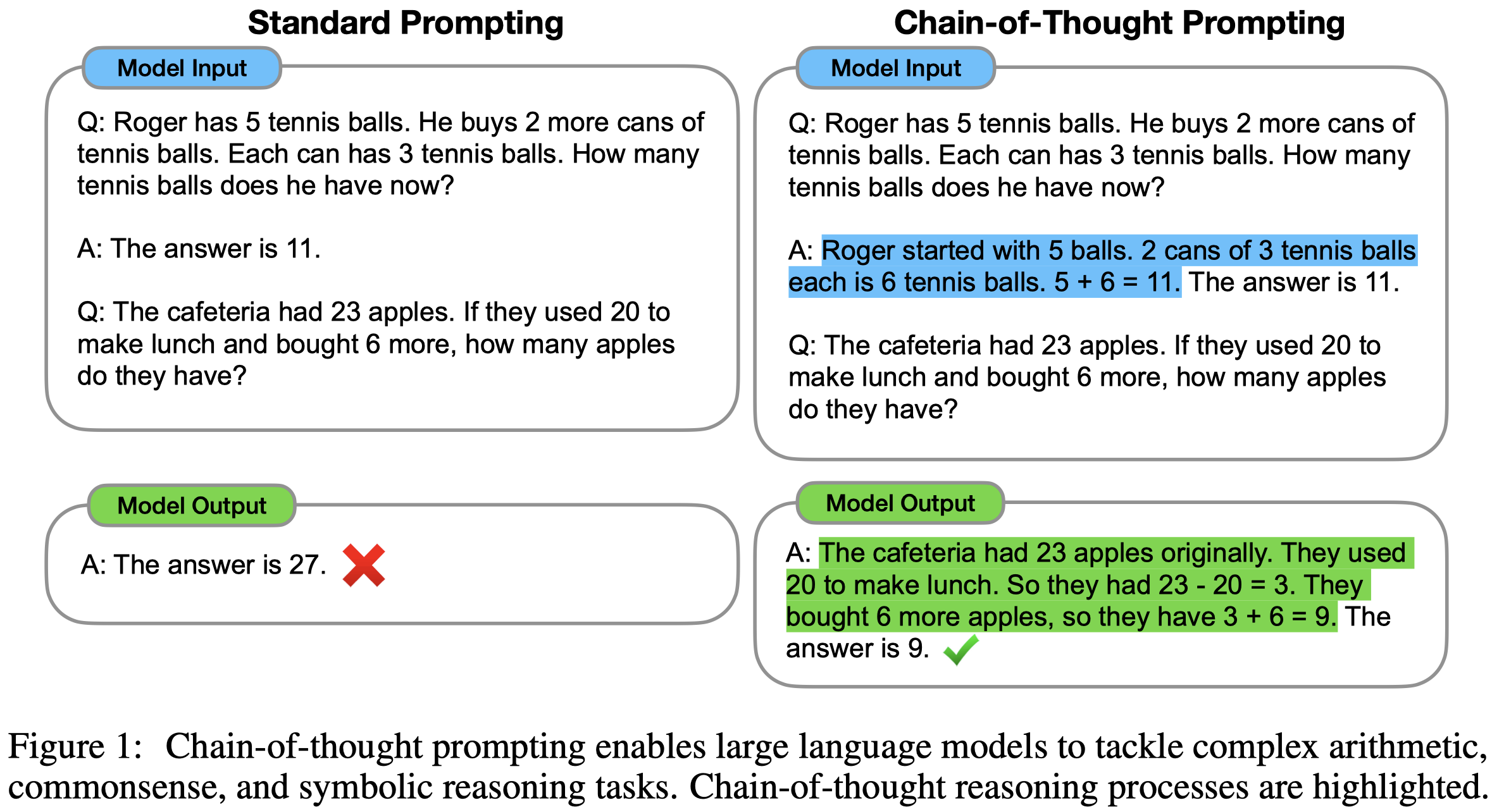
思考和推理的过程像是一个chain,因此叫做chain of thought。即使出现的prompt样例中的中间step看起来只是一段话,但它本质上仍然表达了思维链的过程。
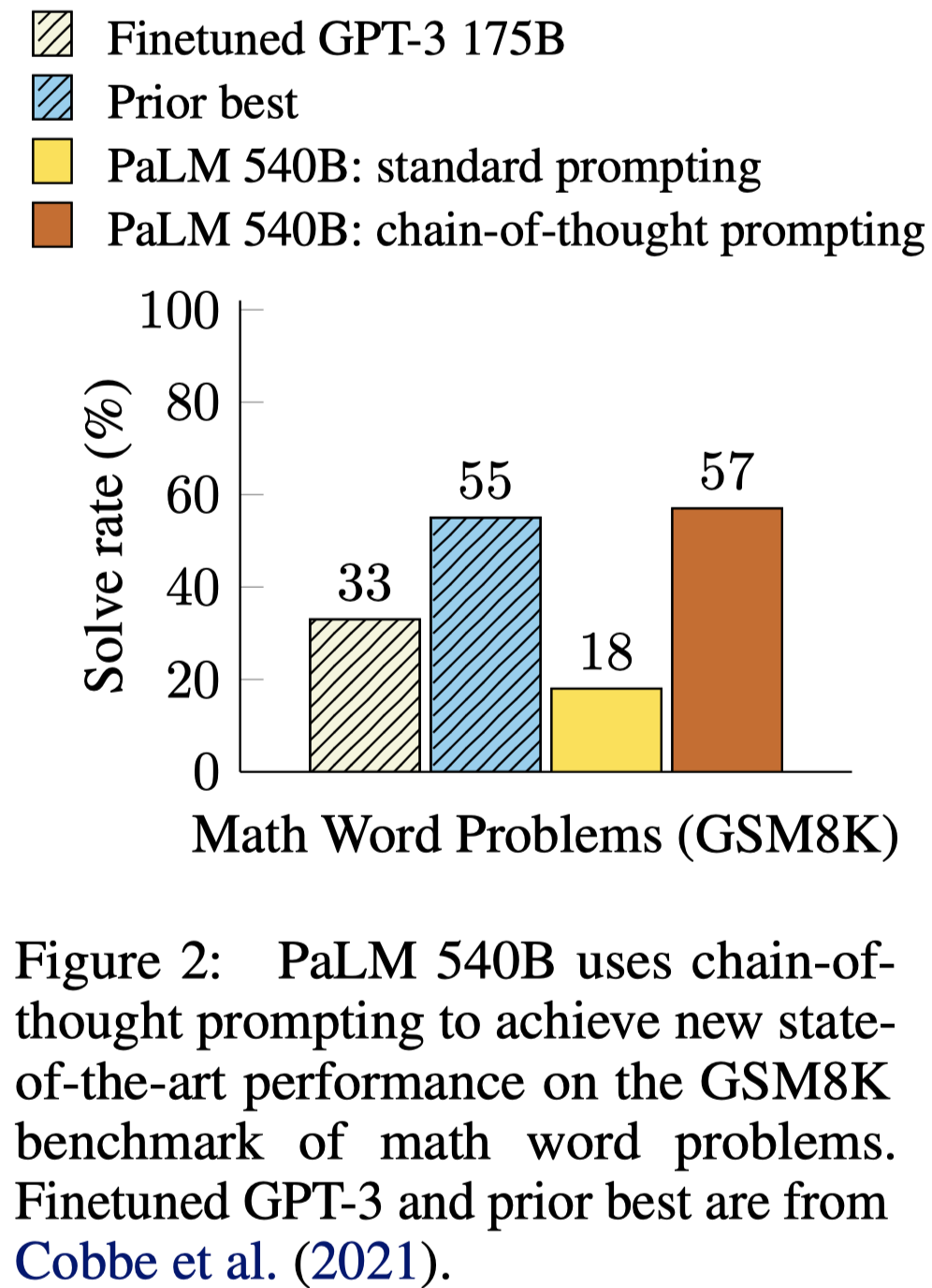
实验结果显示,通过无训练的CoT prompting方法,可以让PaLM 540B在数学问题上达到sota:
CoT有个潜在的假设/前提,某个任务的输入到输出过程,是可以用自然语言的形式进行描述的。
CoT的几个好处:
- First, chain of thought, in principle, allows models to decompose multi-step problems into intermediate steps, which means that additional computation can be allocated to problems that require more reasoning steps.
- Second, a chain of thought provides an interpretable window into the behavior of the model, suggesting how it might have arrived at a particular answer and providing opportunities to debug where the reasoning path went wrong (although fully characterizing a model’s computations that support an answer remains an open question).
- Third, chain-of-thought reasoning can be used for tasks such as math word problems, commonsense reasoning, and symbolic manipulation, and is potentially applicable (at least in principle) to any task that humans can solve via language.
- Finally, chain-of-thought reasoning can be readily elicited in sufficiently large off-the-shelf language models simply by including examples of chain of thought sequences into the exemplars of few-shot prompting.
Zero-shot CoT
Large Language Models are Zero-Shot Reasoners. The University of Tokyo and google. NeurIPS 2022.
Pretrained large language models (LLMs) are widely used in many sub-fields of natural language processing (NLP) and generally known as excellent few-shot learners with task-specific exemplars. Notably, chain of thought (CoT) prompting, a recent technique for eliciting complex multi-step reasoning through step-by-step answer examples, achieved the state-of-the-art performances in arithmetics and symbolic reasoning, difficult system-2 tasks that do not follow the standard scaling laws for LLMs. While these successes are often attributed to LLMs’ ability for few-shot learning, we show that LLMs are decent zero-shot reasoners by simply adding “Let’s think step by step” before each answer. Experimental results demonstrate that our Zero-shot-CoT, using the same single prompt template, significantly outperforms zero-shot LLM performances on diverse benchmark reasoning tasks including arithmetics (MultiArith, GSM8K, AQUA-RAT, SVAMP), symbolic reasoning (Last Letter, Coin Flip), and other logical reasoning tasks (Date Understanding, Tracking Shuffled Objects), without any hand-crafted few-shot examples, e.g. increasing the accuracy on MultiArith from 17.7% to 78.7% and GSM8K from 10.4% to 40.7% with large-scale InstructGPT model (text-davinci002), as well as similar magnitudes of improvements with another off-the-shelf large model, 540B parameter PaLM. The versatility of this single prompt across very diverse reasoning tasks hints at untapped and understudied fundamental zero-shot capabilities of LLMs, suggesting high-level, multi-task broad cognitive capabilities may be extracted by simple prompting. We hope our work not only serves as the minimal strongest zero-shot baseline for the challenging reasoning benchmarks, but also highlights the importance of carefully exploring and analyzing the enormous zero-shot knowledge hidden inside LLMs before crafting finetuning datasets or few-shot exemplars.
Issue:最近提出的CoT是few-shot的
Solution:作者发现,LLM是可以实现zero-shot CoT的,通过添加一个简单的prompt:Let’s think step by step。
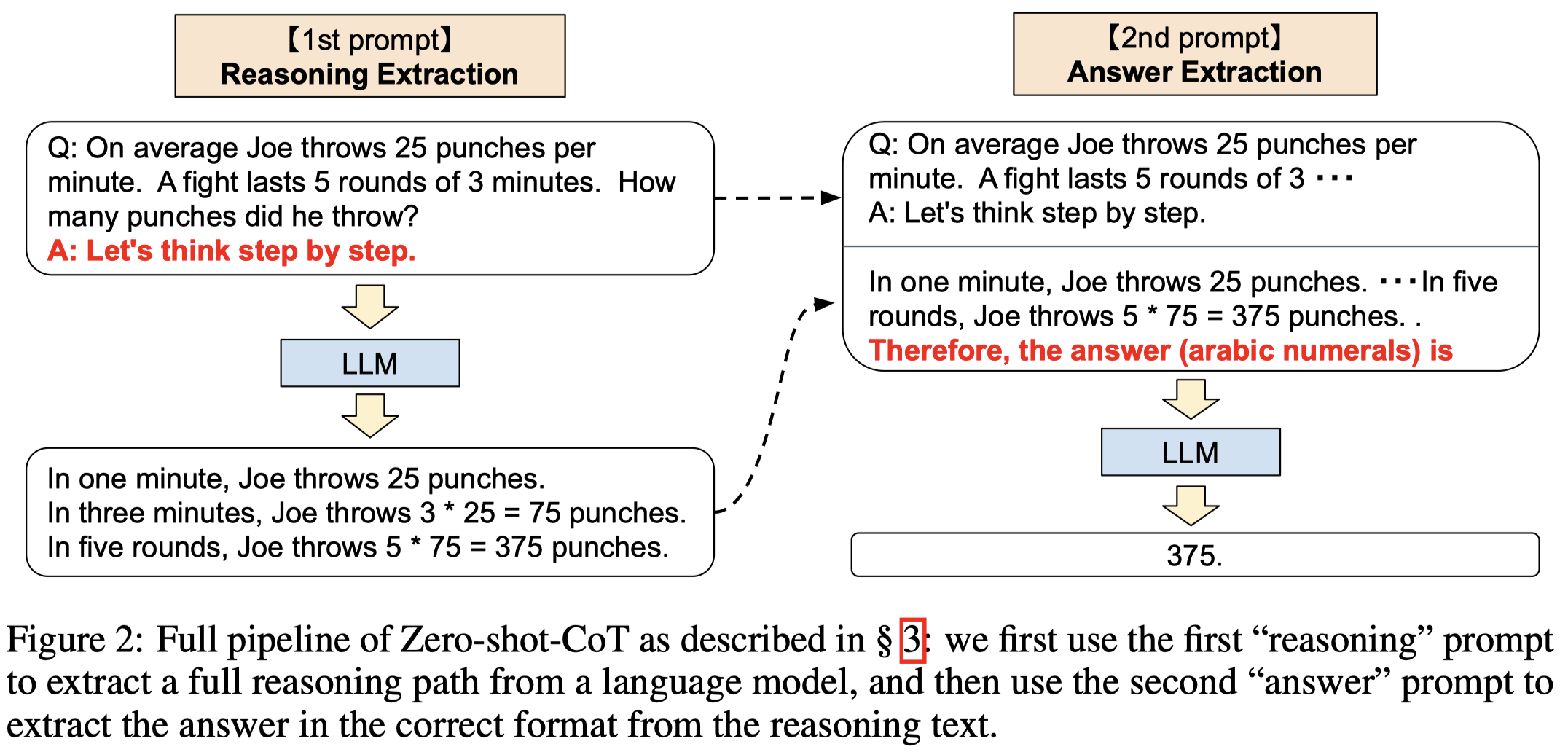
作者的方法包括两步,第一步是获取CoT结果;第二步是将上一步的CoT加入到input prompt,获取最后的答案:
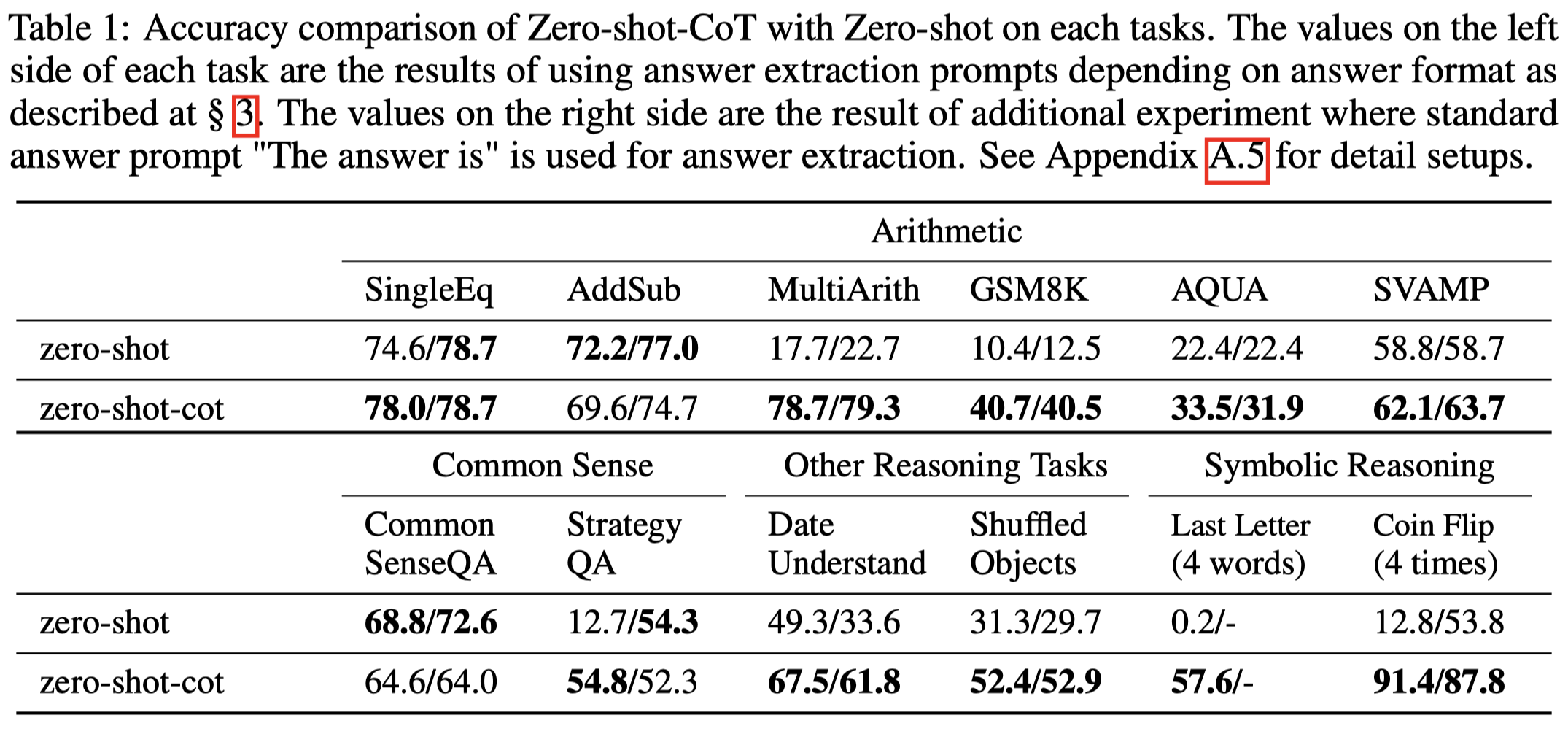
实验结果:
不同提示prompt的选择:
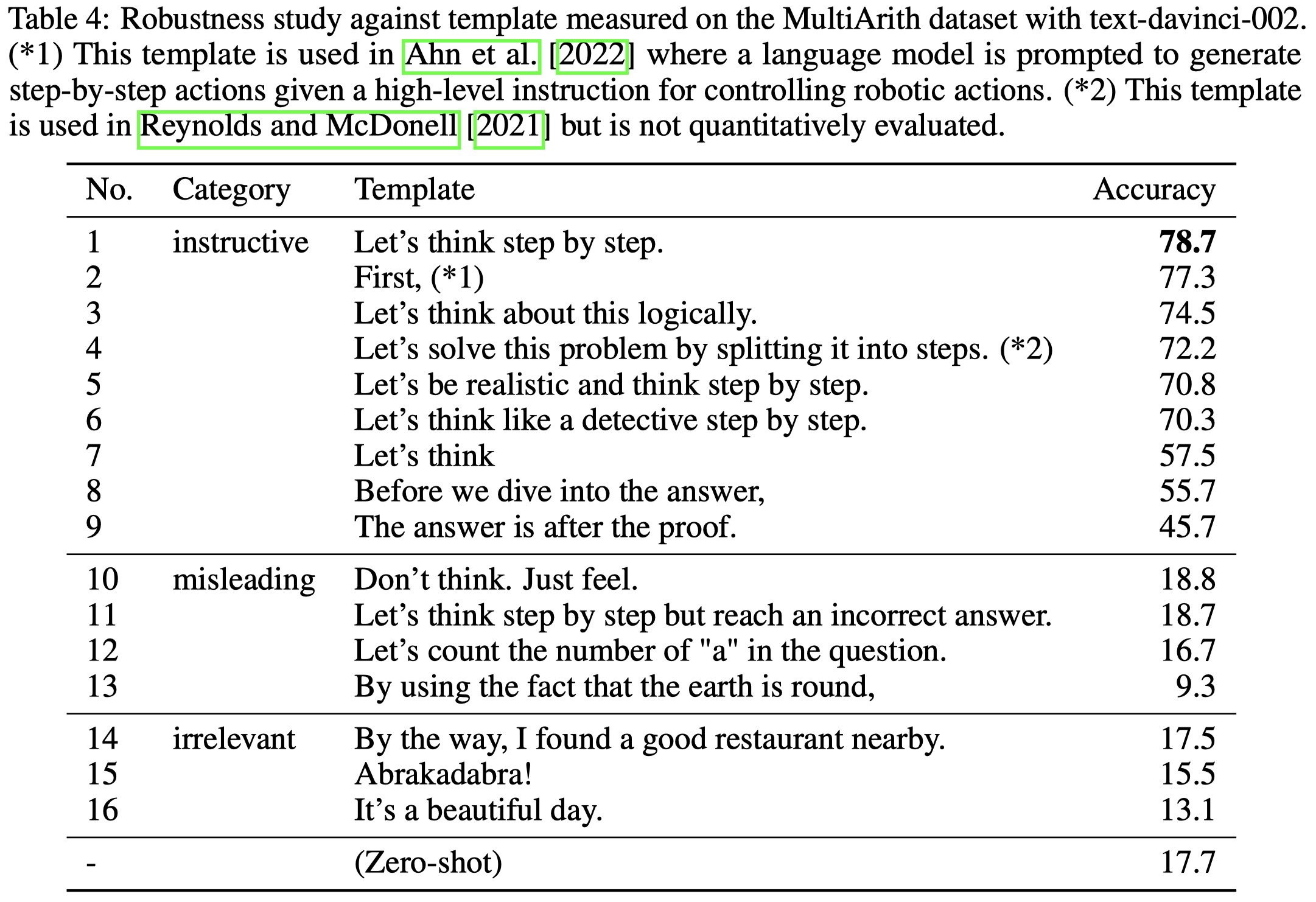
观察:
- 如果提示中加入了分步地思考这种语义,效果会明显的提升
Self-Verification
Large Language Models are Better Reasoners with Self-Verification
arXiv 2013
Recently, with the chain of thought (CoT) prompting, large language models (LLMs), e.g., GPT-3, have shown strong reasoning ability in several natural language processing tasks such as arithmetic, commonsense, and logical reasoning. However, LLMs with CoT require multi-step prompting and multi-token prediction, which is highly sensitive to individual mistakes and vulnerable to error accumulation. The above issues make the LLMs need the ability to verify the answers. In fact, after inferring conclusions in some thinking decision tasks, people often check them by re-verifying steps to avoid some mistakes. In this paper, we propose and prove that LLMs also have similar self-verification abilities. We take the conclusion obtained by CoT as one of the conditions for solving the original problem. By taking turns masking the original conditions and predicting their results, we calculate an explainable answer verification score based on whether the re-predicted conditions are correct. Experimental results demonstrate that the proposed method can improve the reasoning performance on various arithmetic, commonsense, and logical reasoning datasets. Our code is publicly available at: https://github.com/WENGSYX/Self-Verification.
使用CoT能够提升LLM的推理能力,但是CoT prompting方法对于个别的小的mistake很敏感从而会出现错误的结果。另外考虑到多次输入相同的prompt,LLM也可能出现不同的推理结果。因此如何从LLM的推理结果中找出正确的答案是很重要的。
之前修正多步推理过程中出现的错误的方法,是training一个额外的验证器verifier。这种做法一方面要求有对应的标注数据;另一方面训练出来的验证器本身又是难以解释的,可靠性难以评估。 因此作者提出了自我验证Self-Verification,无需训练的思路。即让LLM自己验证自己的推理结果。这种做法实际人类也经常做,humans often perform self-verification of inferred conclusions to mitigate mistakes。
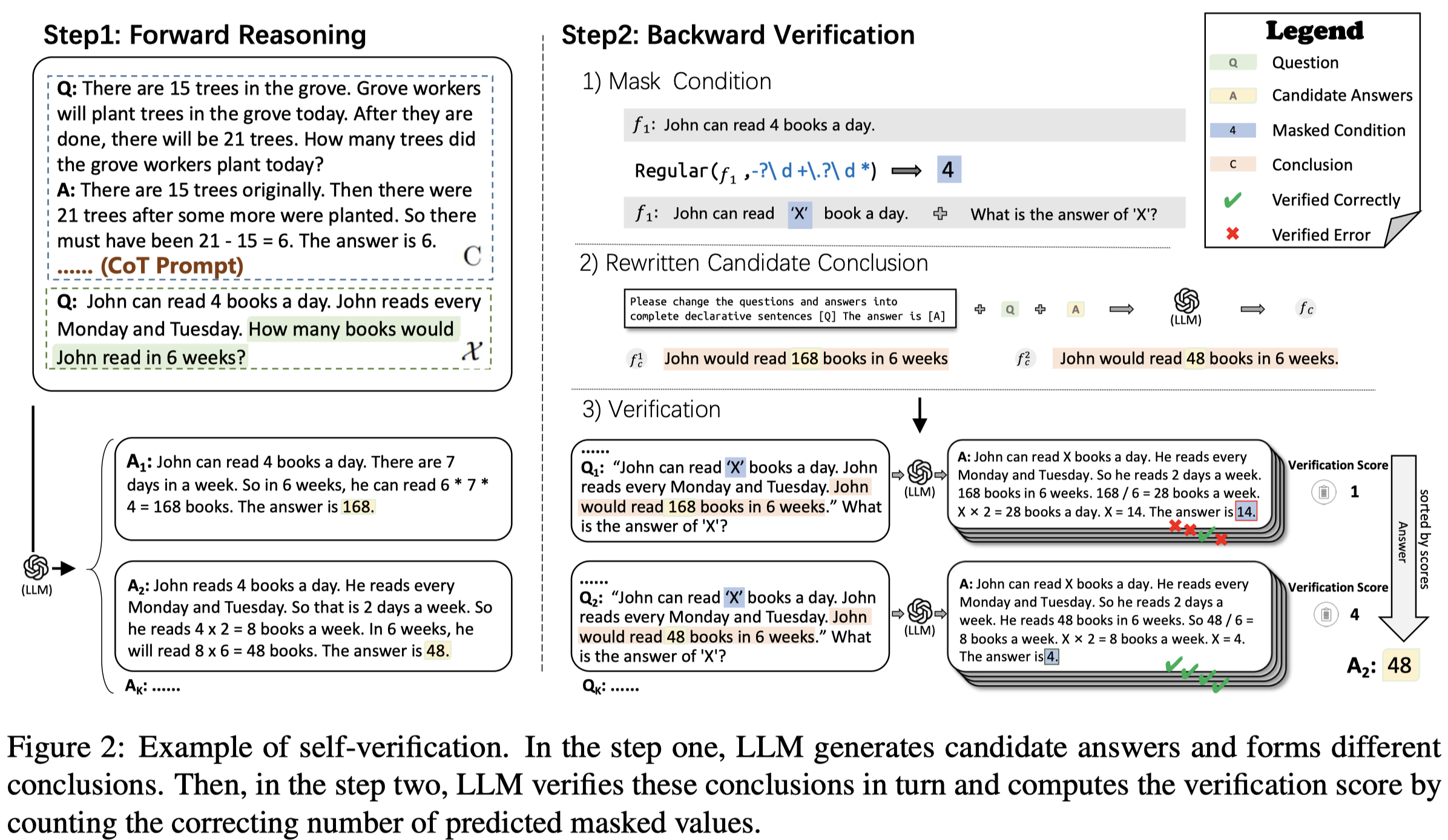
作者的方法有两步:
- Forward Reasoning:通过CoT prompting让LLM生成candidate answers,即从conditions推导出conclusions,\(X\rightarrow Y\)
- Backward Verification:验证上一步的多个候选答案,mask原来的condition,根据LLM推理出的答案,推导被mask掉的condition。准确预测出来的condition越多,验证得分越高。最后选择验证得分最大的答案。\(Y\rightarrow X\)
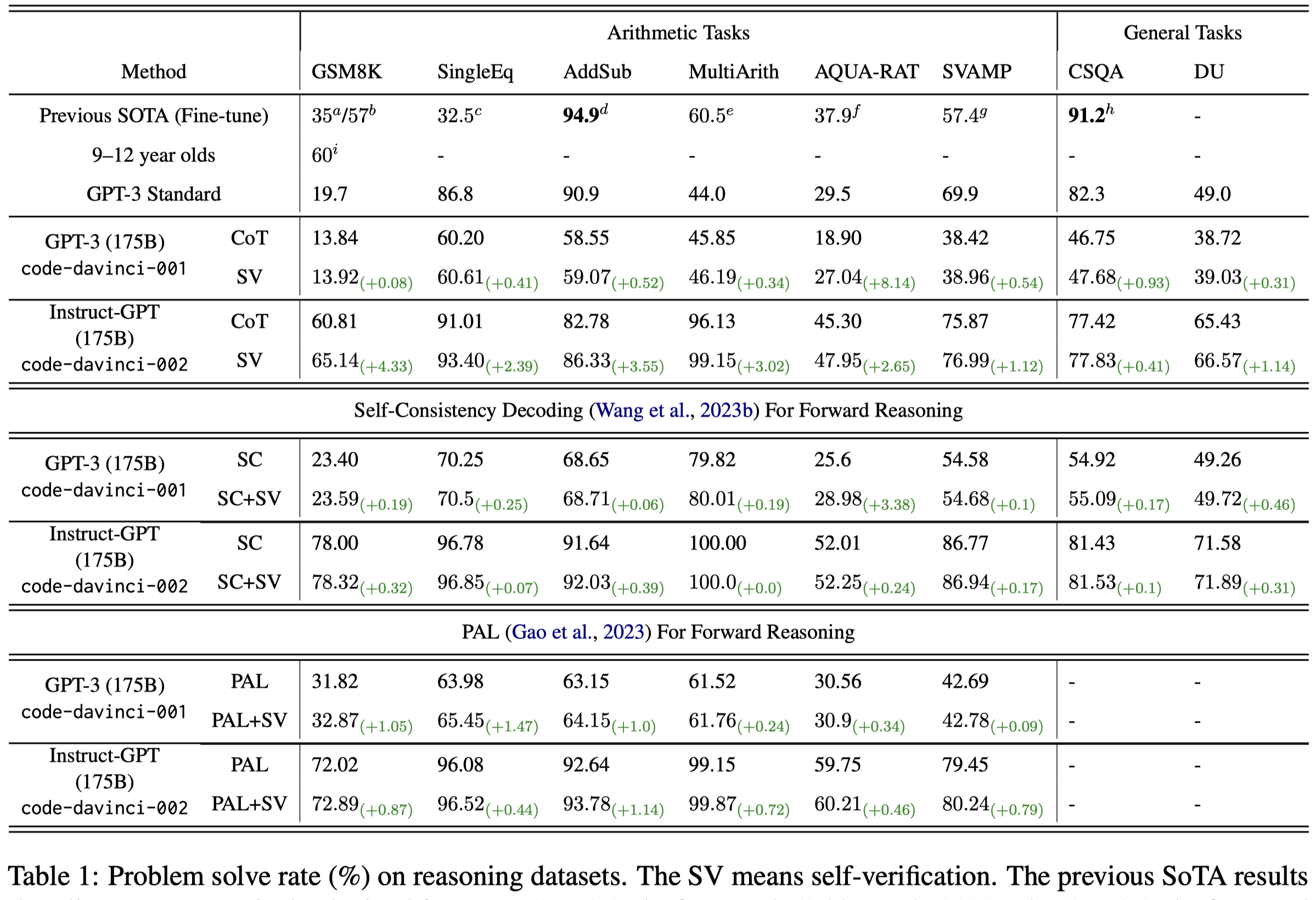
实验结果:
Self-Consistency CoT
Self-Consistency Improves Chain of Thought Reasoning in Language Models
ICLR 2023,Google research
Chain-of-thought prompting combined with pre-trained large language models has achieved encouraging results on complex reasoning tasks. In this paper, we propose a new decoding strategy, self-consistency, to replace the naive greedy decoding used in chain-of-thought prompting. It first samples a diverse set of reasoning paths instead of only taking the greedy one, and then selects the most consistent answer by marginalizing out the sampled reasoning paths. Self-consistency leverages the intuition that a complex reasoning problem typically admits multiple different ways of thinking leading to its unique correct answer. Our extensive empirical evaluation shows that self-consistency boosts the performance of chain-of-thought prompting with a striking margin on a range of popular arithmetic and commonsense reasoning benchmarks, including GSM8K (+17.9%), SVAMP (+11.0%), AQuA (+12.2%), StrategyQA (+6.4%) and ARC-challenge (+3.9%).
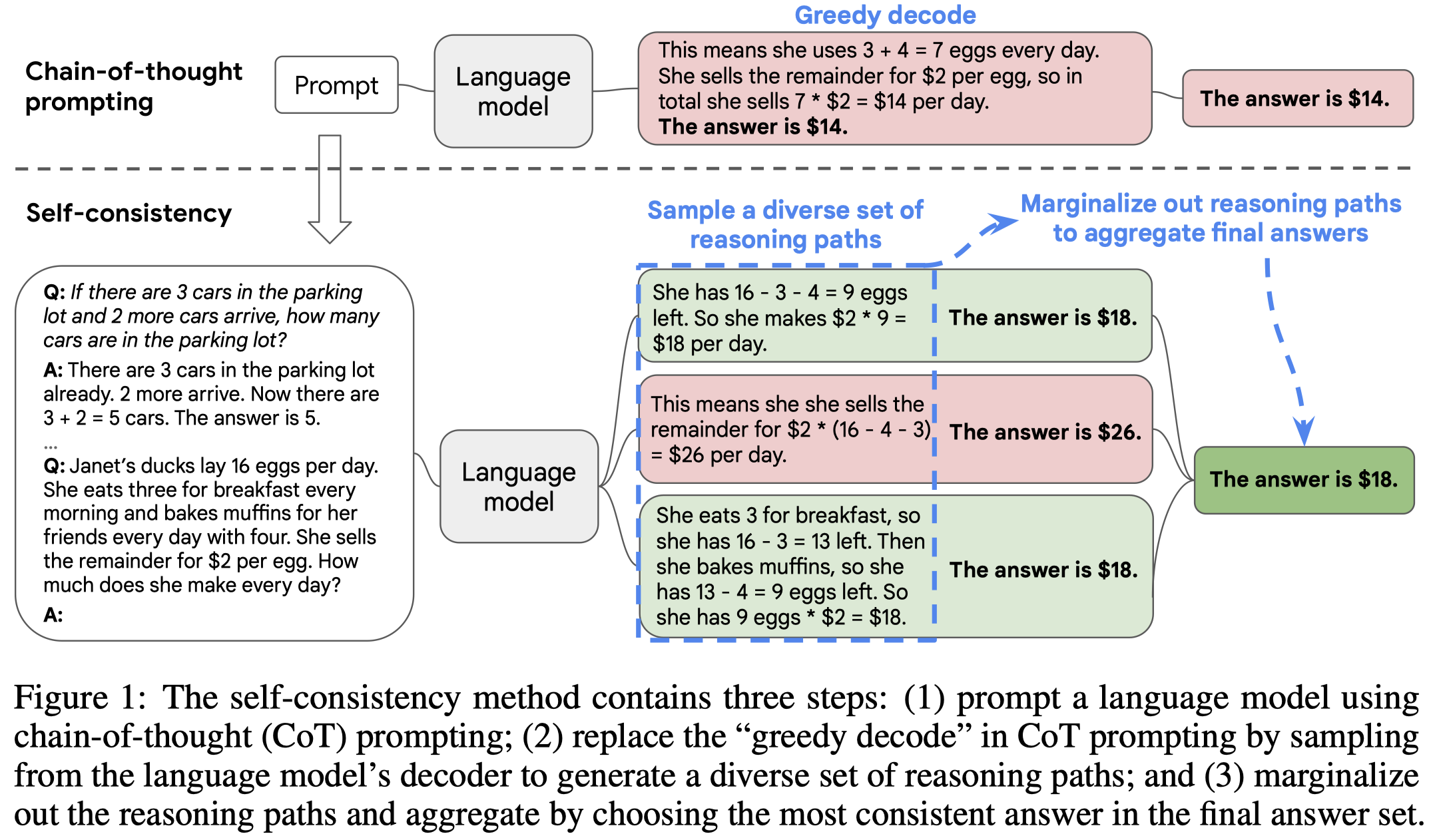
原始的CoT prompting方法是直接生成唯一的推理路径和对应的答案,这种策略可以叫做是greedy decoding strategy,即取推理路径中概率最大的策略。
这篇论文提出一种新的decoding策略 Self-Consistency,它的直觉是一个复杂的推理任务,可能有多种推理路径能够得到最终的答案。越复杂的问题,能够获得最终答案的推理路径可能多样性越大。正确的推理路径不是唯一的。
Self-Consistency的方法很简单,就是让LLM生成多个可能的推理路径和答案,然后选择其中最consistent的答案。作者采用了majority vote的策略,因此最终选择候选答案中出现次数最多的那个答案:
方法很简单,不过论文中有一些发现值得思考:
这是一种类似于self-ensemble的方法,集成一个model的多个预测结果
推理路径的出现概率,可以通过每个位置上token的出现概率之和进行估计:
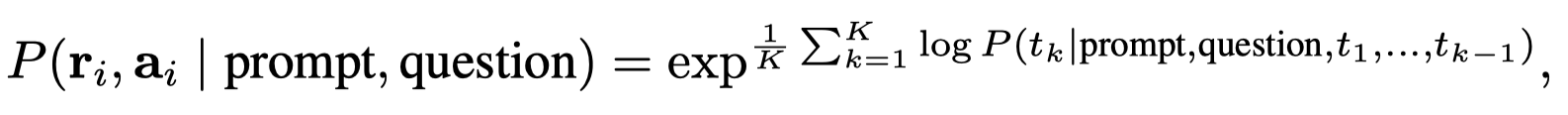
作者发现这样子计算出来的各个推理路径的概率值互相之间很接近,没有太大差距。这证明了LLM实际上没有能力评估出不同solution之间有什么差异。因此,使用这种推理路径的概率去选择最后的答案,和直接认为每个推理路径的权重是1的效果差别不大
直观的说,self-consistency能够适应的推理任务是答案唯一的情况。不过也可以考虑拓展,比如比较生成的文本之间是否矛盾或者冲突,然后选择互相之间最不冲突的文本
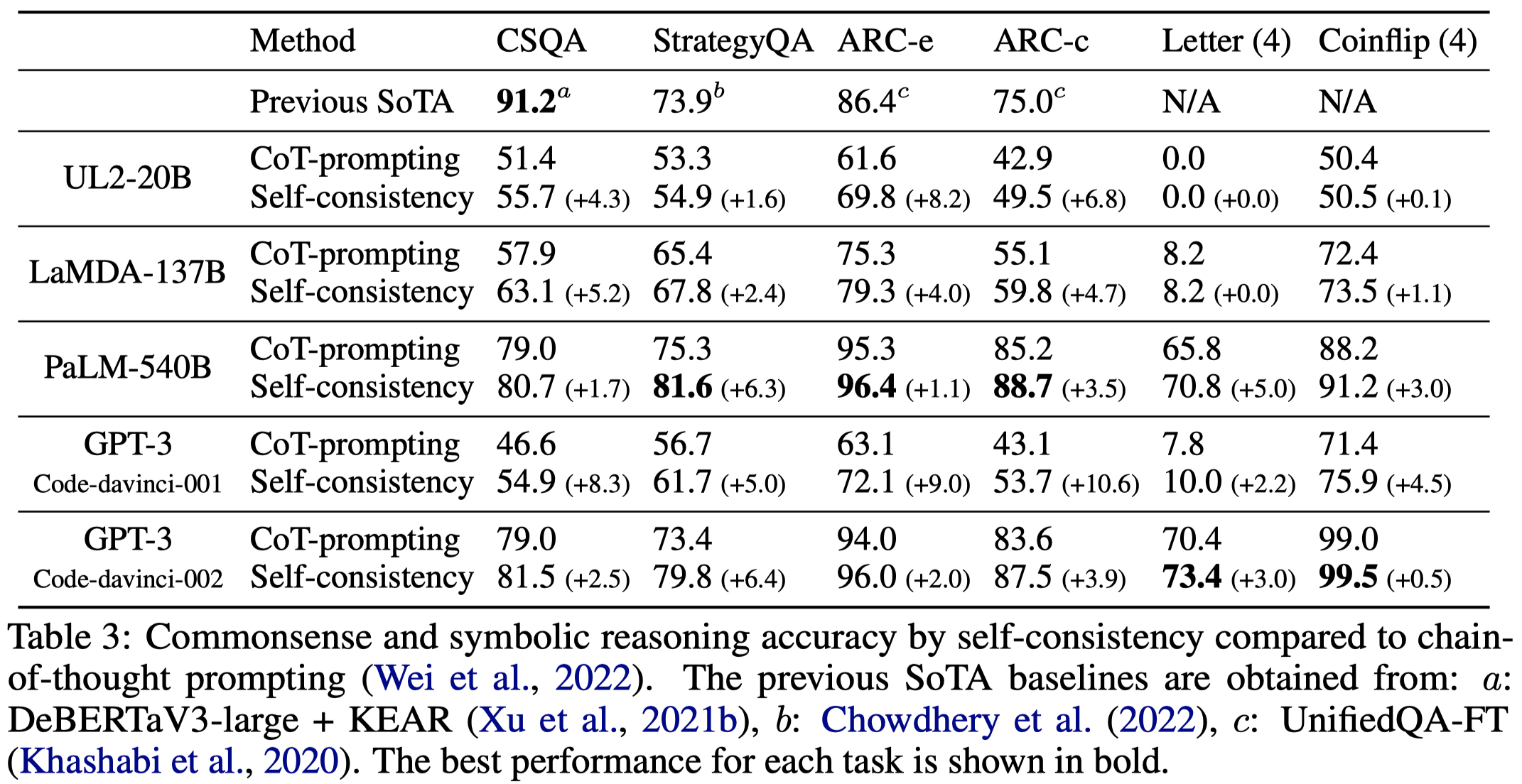
部分实验结果:
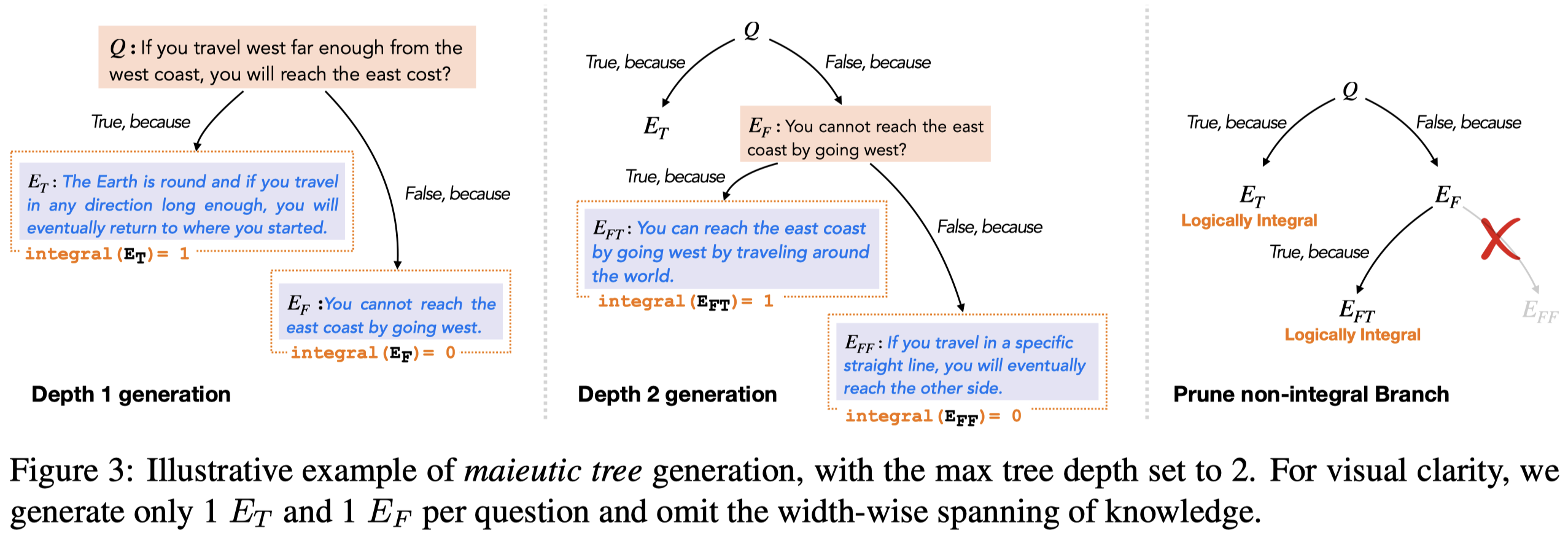
Maieutic Prompting
Maieutic Prompting: Logically Consistent Reasoning with Recursive Explanations
华盛顿大学,EMNLP 2022,代码。
Pre-trained language models (LMs) struggle with consistent reasoning; recently, prompting LMs to generate explanations that self-guide the inference has emerged as a promising direction to amend this. However, these approaches are fundamentally bounded by the correctness of explanations, which themselves are often noisy and inconsistent. In this work, we develop Maieutic Prompting, which aims to infer a correct answer to a question even from the unreliable generations of LM. Maieutic Prompting induces a tree of explanations abductively (e.g. X is true, because . . .) and recursively, then frames the inference as a satisfiability problem over these explanations and their logical relations. We test Maieutic Prompting for true/false QA on three challenging benchmarks that require complex commonsense reasoning. Maieutic Prompting achieves up to 20% better accuracy than state-of-the-art prompting methods, and as a fully unsupervised approach, performs competitively with supervised models. We also show that M AIEUTIC PROMPTING improves robustness in inference while providing interpretable rationales.
虽然之前的paper常常假设LLM可以模拟人类的推理能力。但是实际上目前还做不到。LLM的推理是常常自相矛盾的,不可依赖的:
- the explanation does not logically lead to the inferred answer 解释和答案不一致
- the model infers the same label for a statement and its negation 相反的解释有相同的答案
- falsifies its own generated explanation 篡改/伪造自己的解释

作者是受到了maieutic method的启发,逐步的确认和消除有矛盾的假设:
Maieutic method brings out definitions implicit in the interlocutor’s beliefs, ... is a method of hypothesis elimination, steadily identifying and eliminating those that lead to contradictions (Vlastos, 1991).
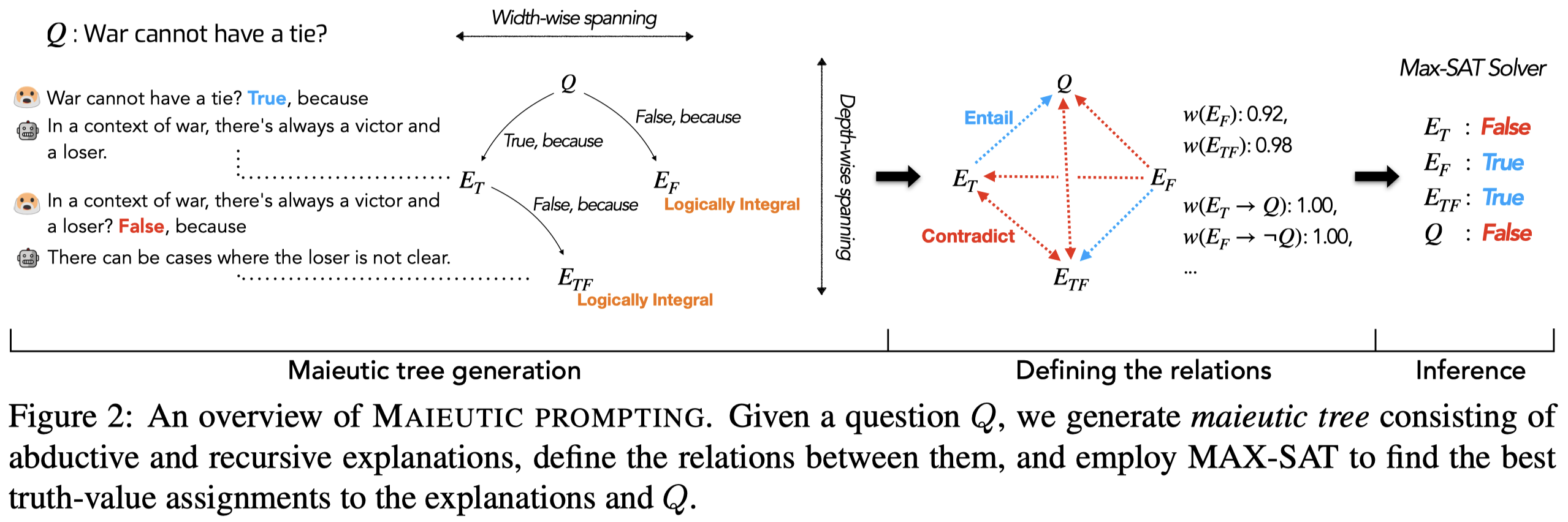
一般的CoT prompting的方法对于某个答案是True/False的问题,通常让LLM先给出解释,再给出答案/预测标签(这称为ad-hoc approach,事前解释)。这种方法生成的explanation是a discriminative explanation that helps in choosing one label over the other。
相反,作者让LLM对True/False给出事后解释。也就是先给定True/False,让LLM给出对应的explanation。这种Abductive generation的方式能够让LLM分别考虑不同的答案的可能性,而不是直接做选择。另外一个好处是,给定的True/False的label information,能够诱导LLM给出更加具体specific的解释。
作者提出的一个重要观点是验证LLM生成的propositions的逻辑完整性/完备性logically integral:
We formalize this idea as logical integrity: a proposition \(Q\) is logically integral when the LM consistently infers the truth value of \(Q\) and \(\neg Q\) (i.e. \(Q\) as True and \(\neg Q\) as False, or vice versa)
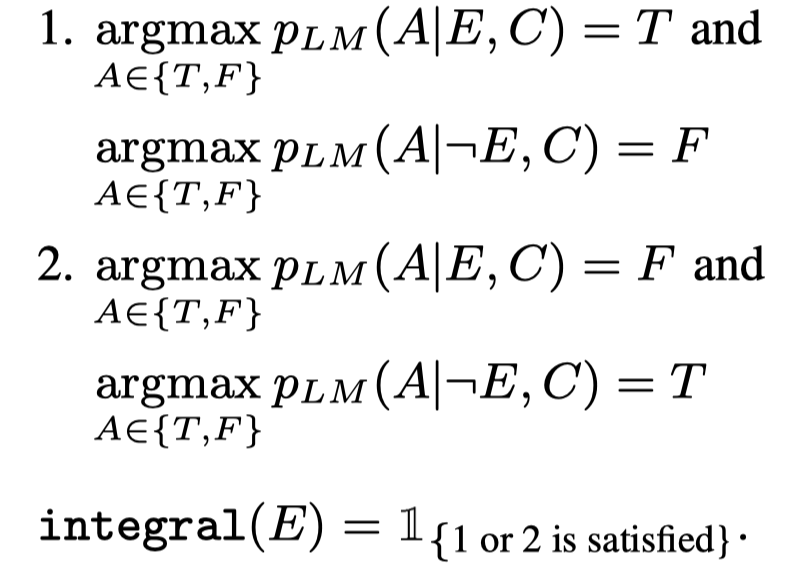
也就是说对于某个LLM生成的proposition \(Q\),LLM不能认为\(Q\)和\(\neg Q\)同时成立。
满足logically integral的解释,作者认为是更加可靠的解释。只有满足logically integral的解释会被保留,然后用于最终的逻辑推理。不满足logically integral的解释,会被继续溯因,迭代的让LLM解释,直至获得logically integral的解释。
对于最后生成的逻辑树,作者评估LLM对于叶子节点解释成立的belief:

以及不同解释之间的关系,作者使用了额外的一个NLI model(RoBERTa fine-tuned on MNLI dataset)去判断任意两个不同explanation之间的关系,权重\(w\)固定为1:
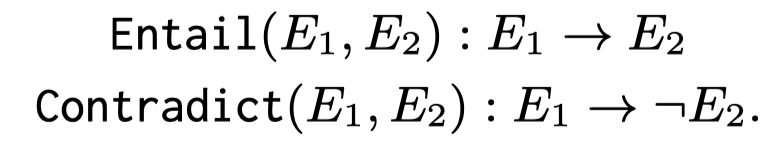
最后使用MAX-SAT去最大程度的满足各种带有权重的条件。
PAL
PAL: Program-aided Language Models
ICML 2023,CMU,代码。
Large language models (LLMs) have demonstrated an impressive ability to perform arithmetic and symbolic reasoning tasks, when provided with a few examples at test time (“few-shot prompting”). Much of this success can be attributed to prompting methods such as “chainof-thought”, which employ LLMs for both understanding the problem description by decomposing it into steps, as well as solving each step of the problem. While LLMs seem to be adept at this sort of step-by-step decomposition, LLMs often make logical and arithmetic mistakes in the solution part, even when the problem is decomposed correctly. In this paper, we present ProgramAided Language models (PA L): a novel approach that uses the LLM to read natural language problems and generate programs as the intermediate reasoning steps, but offloads the solution step to a runtime such as a Python interpreter. With PAL, decomposing the natural language problem into runnable steps remains the only learning task for the LLM, while solving is delegated to the interpreter. We demonstrate this synergy between a neural LLM and a symbolic interpreter across 13 mathematical, symbolic, and algorithmic reasoning tasks from BIG-Bench Hard and others. In all these natural language reasoning tasks, generating code using an LLM and reasoning using a Python interpreter leads to more accurate results than much larger models. For example, PAL using CODEX achieves state-of-the-art few-shot accuracy on GSM8K, surpassing PaLM-540B which uses chain-of-thought by absolute 15% top-1.
这篇文章主要是解决虽然LLM能够理解问题,并且把问题的推理过程分别为不同步骤,但是在最后根据推理过程计算答案的时候出现错误的问题。有时候即便是推理过程是正确的,LLM最后的计算答案是错误的。
因此作者提出对问题的理解,以及推理步骤的拆分和规划让LLM完成。计算答案、根据推理过程推导答案由外部工具完成。这样就能够缓解推理链正确,最后对应的推理结果错误的问题。让LLM做自己擅长的部分,不擅长的部分让其它工具完成。
让LLM生成推理答案的时候同时生成编程语言,最后使用外部的工具如python interpreter计算答案:

Least-to-Most
Least-to-Most Prompting Enables Complex Reasoning in Large Language Models
ICLR 2023, Google research
Chain-of-thought prompting has demonstrated remarkable performance on various natural language reasoning tasks. However, it tends to perform poorly on tasks which requires solving problems harder than the exemplars shown in the prompts. To overcome this challenge of easy-to-hard generalization, we propose a novel prompting strategy, least-to-most prompting. The key idea in this strategy is to break down a complex problem into a series of simpler subproblems and then solve them in sequence. Solving each subproblem is facilitated by the answers to previously solved subproblems. Our experimental results on tasks related to symbolic manipulation, compositional generalization, and math reasoning reveal that least-to-most prompting is capable of generalizing to more difficult problems than those seen in the prompts. A notable finding is that when the GPT-3 code-davinci-002 model is used with least-to-most prompting, it can solve the compositional generalization benchmark SCAN in any split (including length split) with an accuracy of at least 99% using just 14 exemplars, compared to only 16% accuracy with chain-of-thought prompting. This is particularly noteworthy because neural-symbolic models in the literature that specialize in solving SCAN are trained on the entire training set containing over 15,000 examples. We have included prompts for all the tasks in the Appendix.
前面的CoT prompting方法会面临的问题是,如果要解决的问题比CoT中样例的问题更难的话,效果就很差:
However, chain-of-thought prompting has a key limitation—it often performs poorly on tasks that require generalization of solving problems harder than the demonstration examples, such as compositional generalization (Lake & Baroni, 2018; Keysers et al., 2020).
因此,作者提出了一种从简单到复杂,先把问题分解为几个子问题,然后逐步的解决子问题的方法:
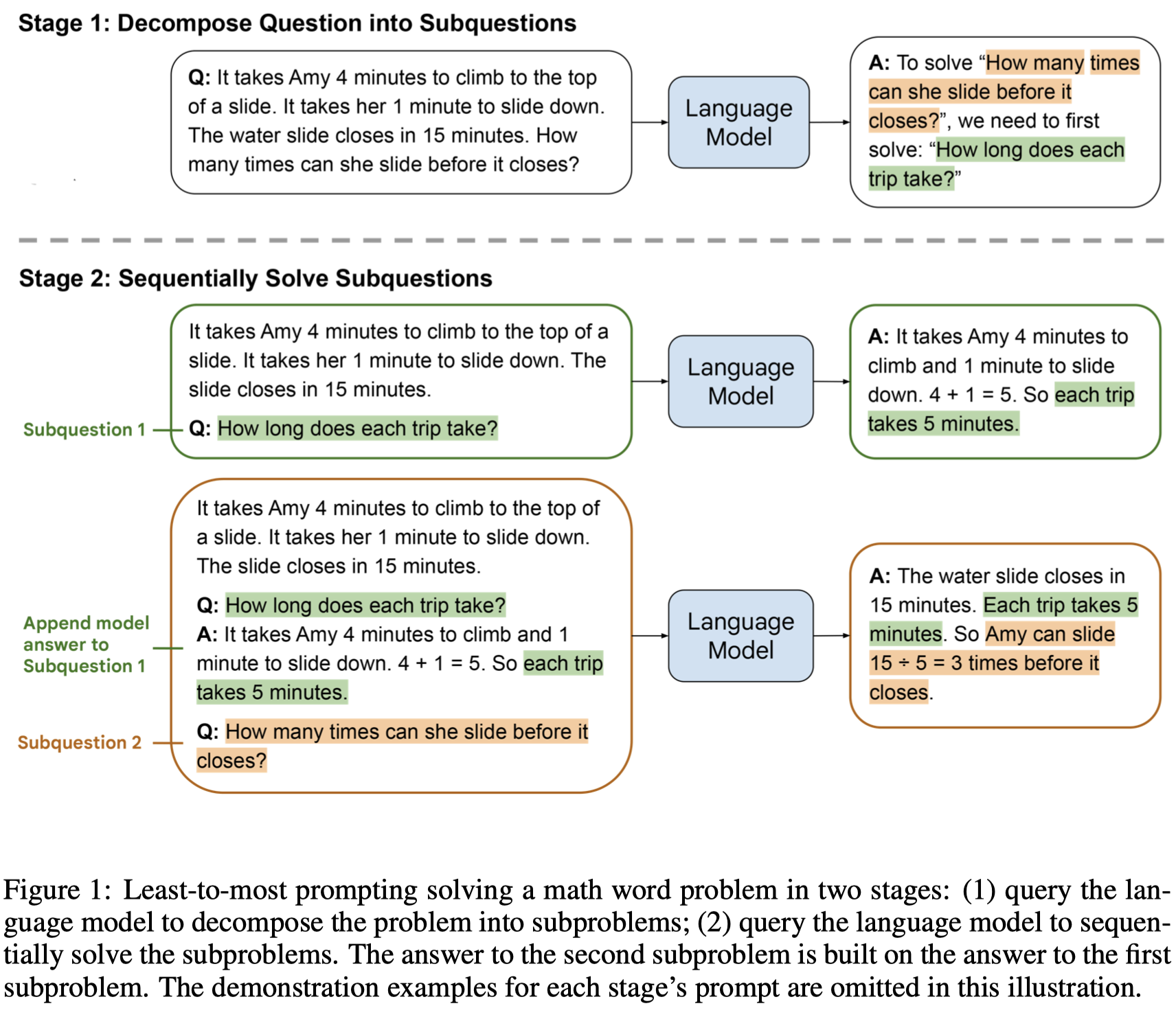
第一步是通过给定几个样例,让LLM把问题分解成几个子问题Decomposition;
第二步是逐步的解决子问题,子问题的答案又附加到prompt上,作为解决下一个子问题的上下文。
- Decomposition. The prompt in this stage contains constant examples that demonstrate the decomposition, followed by the specific question to be decomposed.
- Subproblem solving. The prompt in this stage consists of three parts: (1) constant examples demonstrating how subproblems are solved; (2) a potentially empty list of previously answered subquestions and generated solutions, and (3) the question to be answered next.
CIRS
When Do Program-of-Thought Works for Reasoning? AAAI 2024. 浙大. 代码.
In the realm of embodied artificial intelligence, the reasoning capabilities of Large Language Models (LLMs) play a pivotal role. Although there are effective methods like program-ofthought prompting for LLMs which uses programming language to tackle complex reasoning tasks, the specific impact of code data on the improvement of reasoning capabilities remains under-explored. To address this gap, we propose complexity-impacted reasoning score (CIRS), which combines structural and logical attributes, to measure the correlation between code and reasoning abilities. Specifically, we use the abstract syntax tree to encode the structural information and calculate logical complexity by considering the difficulty and the cyclomatic complexity. Through an empirical analysis, we find not all code data of complexity can be learned or understood by LLMs. Optimal level of complexity is critical to the improvement of reasoning abilities by program-aided prompting. Then we design an autosynthesizing and stratifying algorithm, and apply it to instruction generation for mathematical reasoning and code data filtering for code generation tasks. Extensive results demonstrates the effectiveness of our proposed approach. Code will be integrated into the EasyInstruct framework.
Issue: LLM的推理能力非常重要,最近一些工作利用code prompting的方法,比如program-of-thought来提升LLM的推理能力。但是,到底什么情况下这种基于code的推理可以起作用?
Solution: 作者提出LLM在训练阶段,code的复杂度与LLM本身的推理能力息息相关。
作者认为用编程语言来作为prompting的两个潜在好处:
- their superior modeling of intricate structures compared to serialized natural language.
- their inherent procedure-oriented logic, which assists in addressing multi-step reasoning problems.
作者提出的考虑code data的复杂度,同时从AST结构复杂度和逻辑复杂度两个角度进行考虑,CIRS指标计算如下:
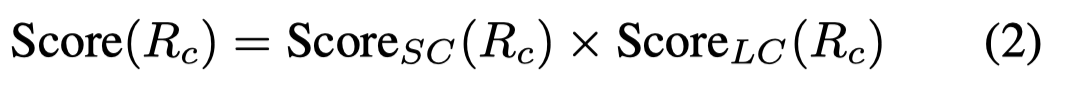
结构复杂度考虑代码抽取语法树的Node Count、Node Types和Tree Depth:

逻辑复杂度考虑代码的Halstead Complexity Metrics (Halstead 1977) and McCabe’s Cyclomatic Complexity (McCabe 1976)圈复杂度:

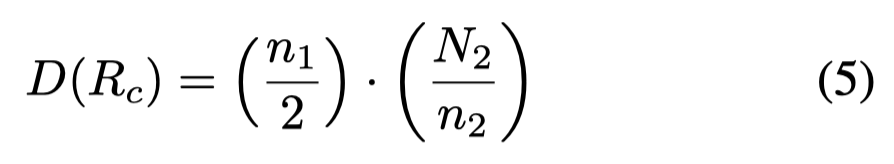

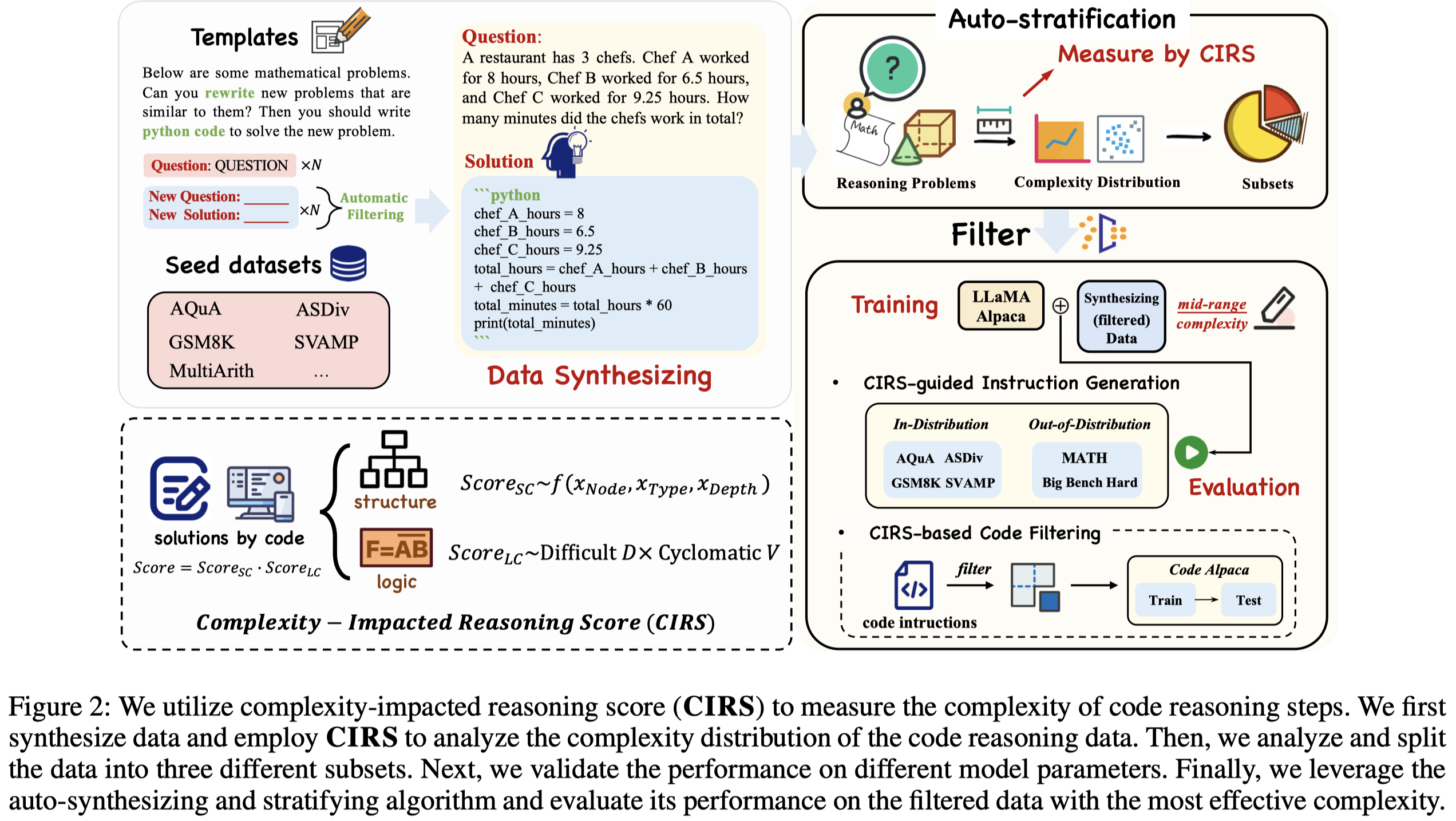
为了进行empirical study,作者利用现有的几个math problem soloving训练集作为seed dataset,然后让gpt-3.5-turbo不断的仿照生成更多的code data以及对应的问题。随后,按照CIRS指标划分出复杂度低、中、高的3个子集,用于训练LLaMA 1。
实验结果:
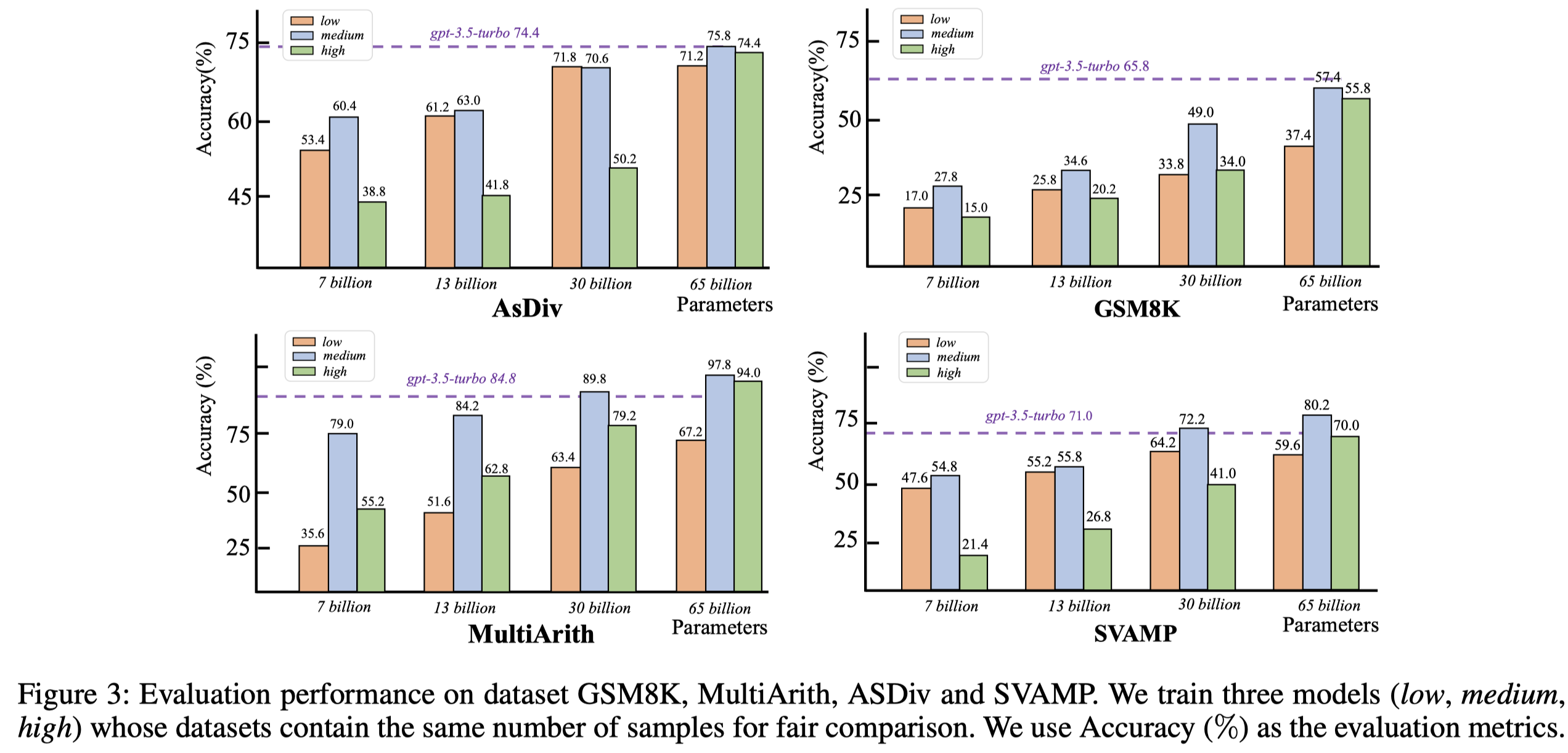
观察:
- 采用中间复杂度的code data训练LLM,效果更好
- 随着参数量增加,LLM越来越能够从复杂的代码中获取足够的好处
- 复杂度过低的code data可能蕴含的知识量太少;而复杂度过高的code data可能对于LLM来说太难理解
ViperGPT
ViperGPT: Visual Inference via Python Execution for Reasoning. ICCV 2023. Columbia University. 代码.
Answering visual queries is a complex task that requires both visual processing and reasoning. End-to-end models, the dominant approach for this task, do not explicitly differentiate between the two, limiting interpretability and generalization. Learning modular programs presents a promising alternative, but has proven challenging due to the difficulty of learning both the programs and modules simultaneously. We introduce ViperGPT, a framework that leverages code-generation models to compose vision-and-language models into subroutines to produce a result for any query. ViperGPT utilizes a provided API to access the available modules, and composes them by generating Python code that is later executed. This simple approach requires no further training, and achieves state-of-the-art results across various complex visual tasks.
Issue: 视觉上的推理可能是分步的,但是目前大多的方法还是end-to-end的,无法进行compositional reasoning。
Solution: 作者创造了一个框架,通过提供给LLM API让LLM利用这些API来组合生成解决问题的程序,每个API通过调研不同的模型(视觉模型GLIP、X-VLM、LLM GPT-3)等实现不同的功能。程序可以用来一步步的组合推理,API可以直接无需训练的利用已有的各种model去解决问题。
NN为什么不适合做多步的推理?比如把NN分为多个modules,然后期望每个module能够执行特定的任务,问题在于这种做法可能依赖于人工的解析器,或者是利用强化学习训练,但这种方法很难优化;另外,多个模块的NN更加难以训练,输出不可预测。
推理与感知分离,然后结合神经-符号方法。尽管思想上是一致的,但是这种方法较难学习和优化。
随后的方法就开始采用了端到端的思路来降低优化难度。最近大模型被加入进来,但是它们都指定了特定的模型。
作者的框架图:
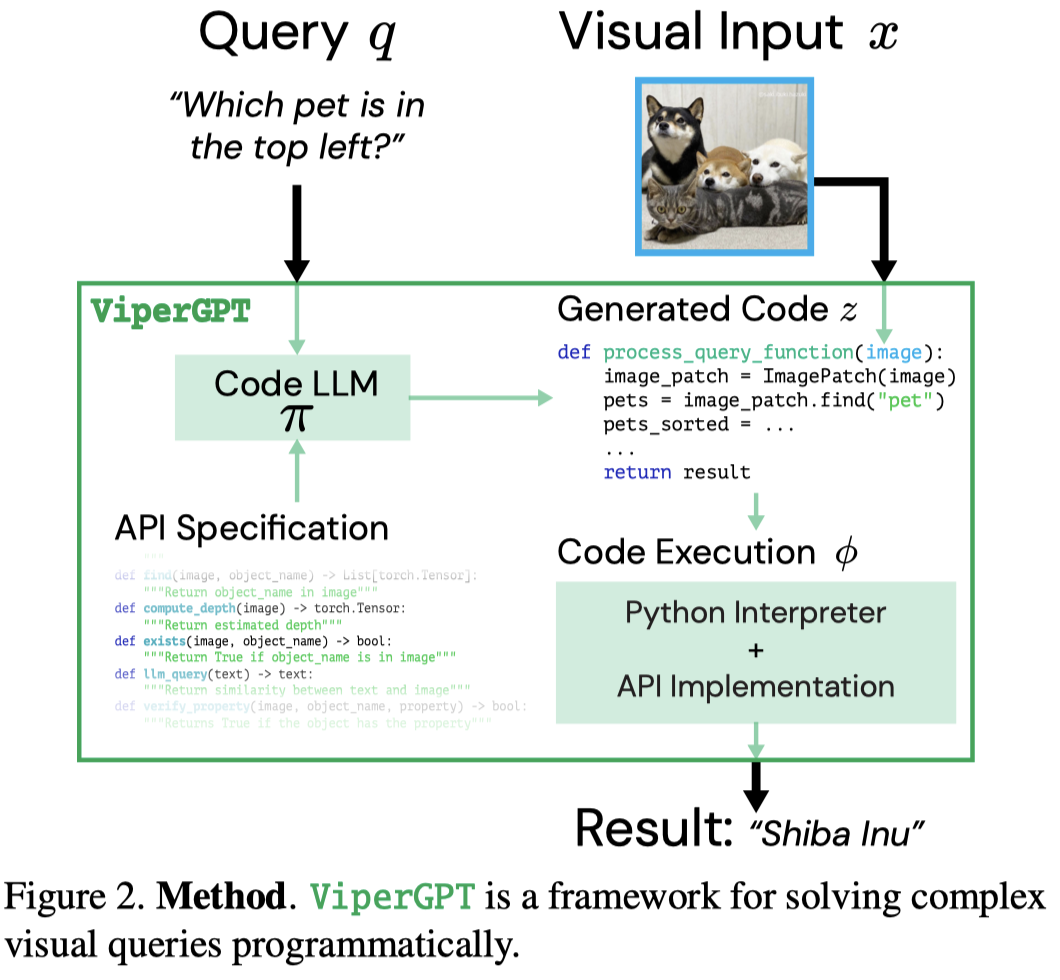
作者的方法可以处理image和video,下面是两个示例:

下面是输入给codex的API prompt,每个class内部的function都有docstring来解释function的目的;然后提供了如何使用这些function的说明示例。输入给Codex的定义没有完整的实现,有两个目的:
- 完整的代码实现可能过长,超出LLM context window size
- 抽象的code定义和具体的实现无关,解耦

最终执行生成的推理程序的时候,同时结合python解释器以及训练好的其它模型。
- python解释器的调研可以利用python各种内置的functions,并且可以完整的执行逻辑操作
- 外部的预训练模型主要负责感知
实验在1) visual grounding, 2) compositional image question answering, 3) external knowledge-dependent image question answering, and 4) video causal and temporal reasoning任务上评估
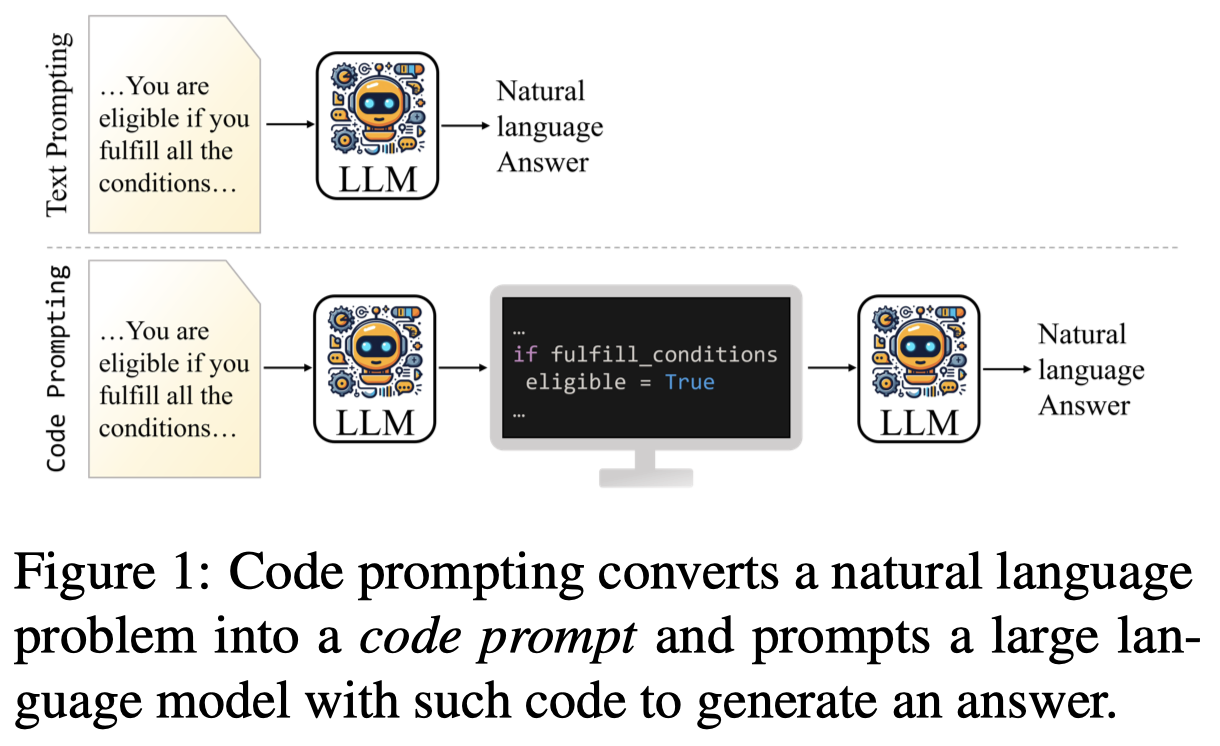
Code Prompt for Conditional Reasoning
Code Prompting Elicits Conditional Reasoning Abilities in Text+Code LLMs. arXiv 2024. hessian.AI. 代码.
Reasoning is a fundamental component of language understanding. Recent prompting techniques, such as chain of thought, have consistently improved LLMs’ performance on various reasoning tasks. Nevertheless, there is still little understanding of what triggers reasoning abilities in LLMs in the inference stage. In this paper, we introduce code prompting, a chain of prompts that transforms a natural language problem into code and directly prompts the LLM using the generated code without resorting to external code execution. We hypothesize that code prompts can elicit certain reasoning capabilities of LLMs trained on text and code and utilize the proposed method to improve conditional reasoning, the ability to infer different conclusions depending on the fulfillment of certain conditions. We find that code prompting exhibits a high-performance boost for multiple LLMs (up to 22.52 percentage points on GPT3.5, 7.75 on Mixtral, and 16.78 on Mistral) across multiple conditional reasoning datasets. We then conduct comprehensive experiments to understand how code prompts trigger reasoning abilities and which capabilities are elicited in the underlying models. Our analysis of GPT3.5 reveals that the code formatting of the input problem is essential for performance improvement. Furthermore, code prompts improve sample efficiency of in-context learning and facilitate state tracking of variables or entities.
Issue: 之前的工作已经证明了,code+code LLM,对于推理问题,可能比text+text LLM效果好,但是是不是code比text能够在text+code LLM上表现效果好还没有进行过探究。
Solution: 作者进行了详细的empirical study来探究,对于conditional reasoning问题,从logical reasoning维度上,code prompt是否能够比text prompt表现好,并且,到底是哪些原因可能导致了code prompt表现效果更好。
QA可以被看作是语义推理任务。conditional reason的定义是给出满足conditions的conclusions,是self-contained的,无需外部的knowledge,属于logical reason的一部分。
作者的方法很直接,利用LLM先将原来自然语言表达的问题转换为code描述的问题,然后再让LLM来执行对应的code。这一个过程与faithful CoT方法一致。
转换后的code,question和doc中的主要entities以局部变量的形式表示,必要满足的条件用if语句来表示,同时原始的question以python comment的方式保存。code prompt和text prompt相比,没有增加任何的新information:

作者的实验主要使用了gpt-35-turbo, Mixtral 7x8B (46.7B), Mistral 7B以及Phi-2 2.7B。在ConditionalQA、BoardgameQA和ShARC三个条件推理数据集上进行了实验。
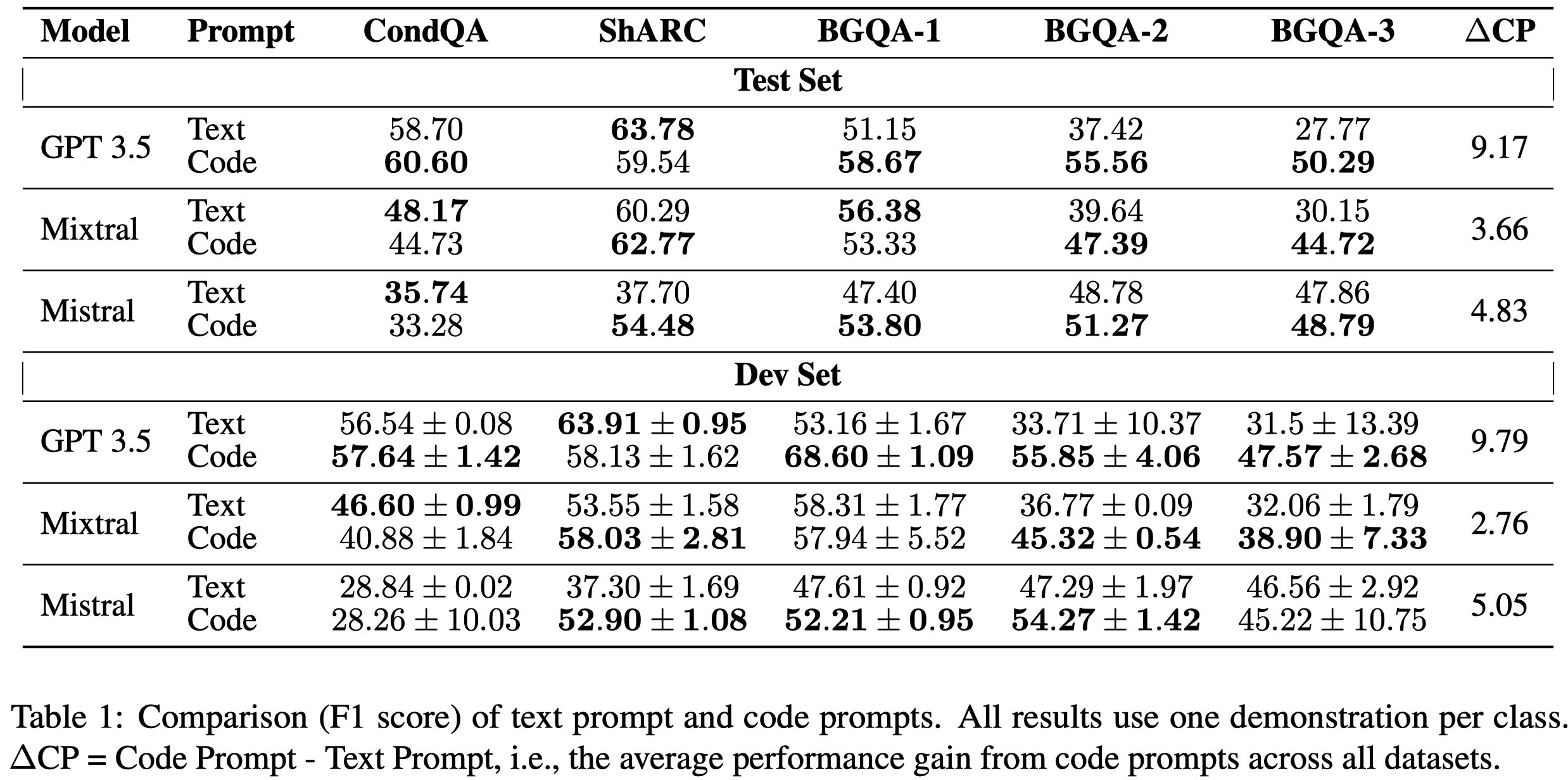
观察与结论:
总体上,code prompt比text prompt表现效果更好
在CondQA这种需要推理能力相对弱一点的数据集上,表现效果提升没有那么大,反而是在BGQA这种需要强推理能力的数据集上表现效果最好。这说明code prompt更加适合于reasoning-intensive的tasks。code prompts elicit conditional reasoning abilities and are most suited for reasoning-intensive tasks
在Phi-2这种小LM上,code prompt效果更好,可能是因为其对于NL问题的推理能力更弱,利用code能够更好的激发推理能力
text prompt的时候,更加不喜欢回答No;而是用code prompt,其更积极的回答No,这可能是因为code prompt更加明确的instruct LLM去跟踪某种状态
作者随后探究了code prompt的syntax是否会与推理性能有影响:
- Atomic Statements:根据FActScore: Fine-grained atomic evaluation of factual precision in long form text generation. EMNLP 2023,将sentence表示为atomic statement,然后append到sentence之后。用来调查是否简化text prompt导致推理能力提升
- Back-Translated Code:把code再度反向翻译回text,用来判断是否是code的semantic,而不是code syntax导致了推理能力提升
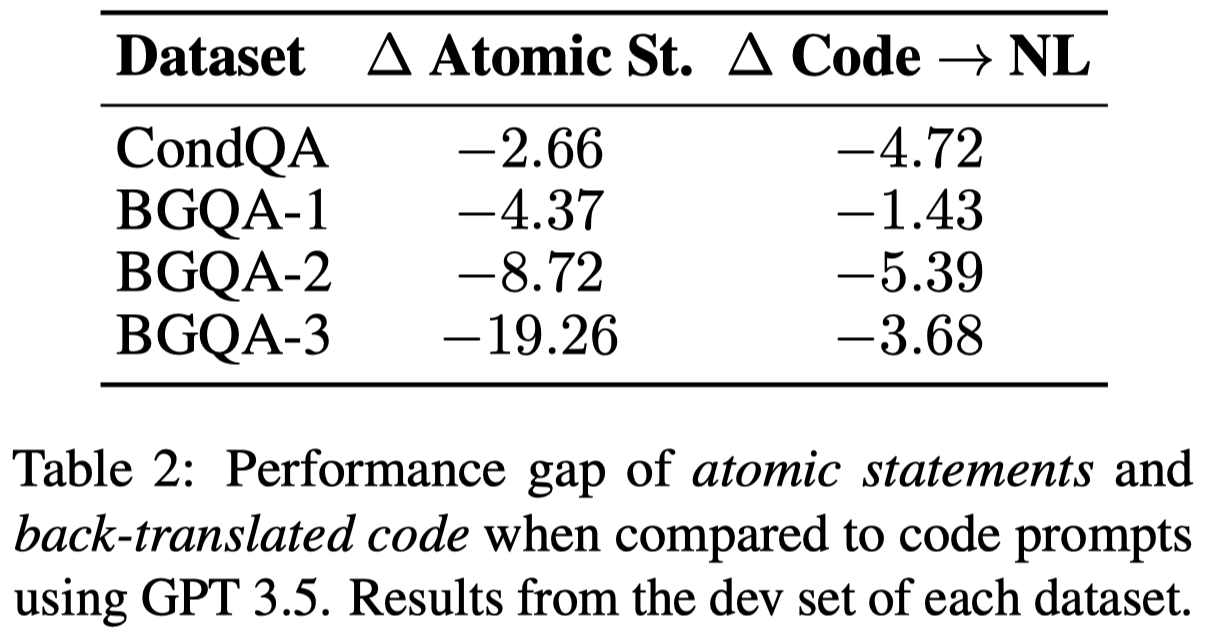
观察:
- code的特定语法,也会对推理能力提升起到作用
然后探究code的semantic是否对效果有影响:
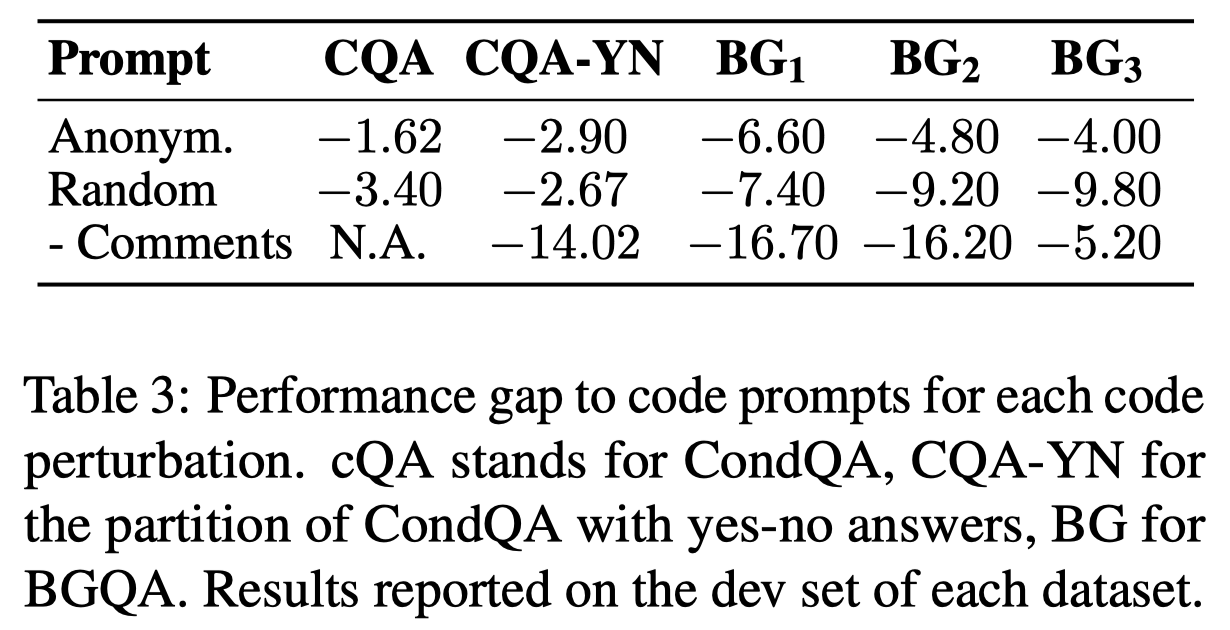
观察:
- code prompt的语义正确也非常关键,特别是应该保留原始的text作为comment
Code Prompts are More Sample-Efficient at Eliciting Reasoning Abilities:
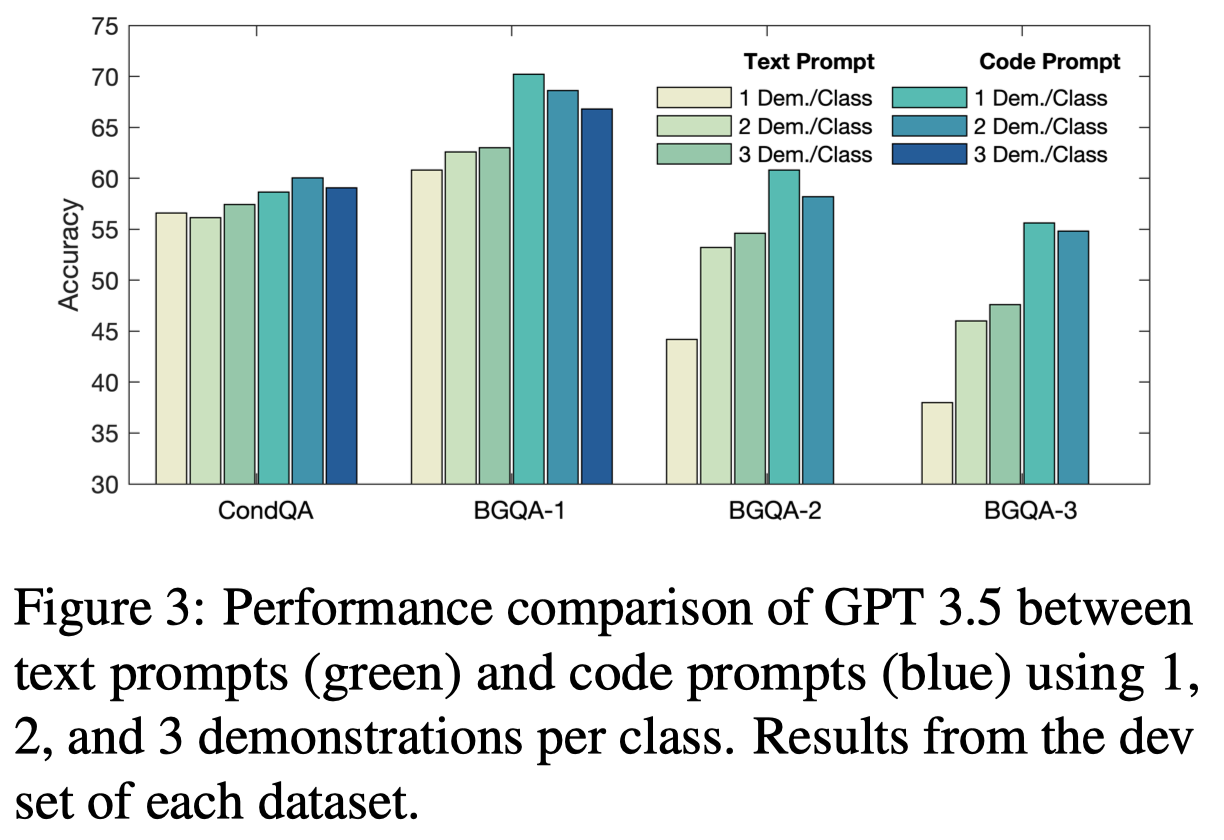
作者推测code prompt的另一个表现好的原因是,它激发了LLM跟踪关键variables/entities的能力。试想一下,如果是纯text,对于预测next token最重要的是周围的local的tokens。但是对于预测code,可能需要参考之前几十行乃至上百行定义的变量。这种跟踪远程entities的能力,对于很多推理问题是重要的。
an improved ability to look for distant co-references caused by training on code can be beneficial for multi-hop reasoning, which is also needed to solve our datasets.
作者通过在LLM输出每一句推理的sentence的时候(以\n结尾),询问LLM在输入中提到的关键key entities,询问其正确还是错误,LLM可以回答True, False, a string, or unknown。
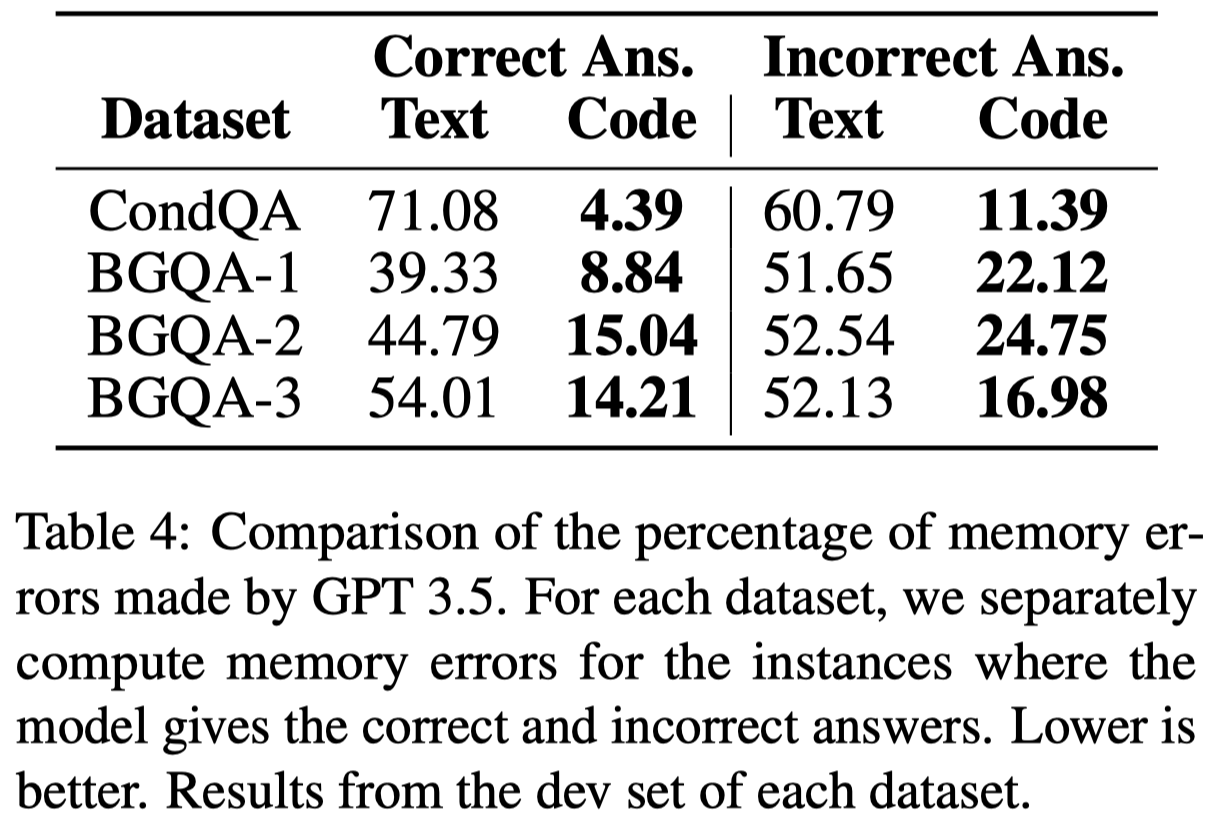
观察:
- Code Prompting improves State Tracking.
Faithful CoT
Faithful Chain-of-Thought Reasoning. IJCNLP 2023. University of Pennsylvania. 代码.
While Chain-of-Thought (CoT) prompting boosts Language Models’ (LM) performance on a gamut of complex reasoning tasks, the generated reasoning chain does not necessarily reflect how the model arrives at the answer (aka. faithfulness). We propose Faithful CoT, a reasoning framework involving two stages: Translation (Natural Language query → symbolic reasoning chain) and Problem Solving (reasoning chain → answer), using an LM and a deterministic solver respectively. This guarantees that the reasoning chain provides a faithful explanation of the final answer. Aside from interpretability, Faithful CoT also improves empirical performance: it outperforms standard CoT on 9 of 10 benchmarks from 4 diverse domains, with a relative accuracy gain of 6.3% on Math Word Problems (MWP), 3.4% on Planning, 5.5% on Multi-hop Question Answering (QA), and 21.4% on Relational Inference. Furthermore, with GPT-4 and Codex, it sets the new state-of-the-art few-shot performance on 7 datasets (with 95.0+ accuracy on 6 of them), showing a strong synergy between faithfulness and accuracy.
Issue: 在CoT被提出的时候[Chain of Thought Prompting Elicits Reasoning in Large Language Models. 2022],被认为provide an interpretable window into the behavior of the model。但是从作者观察到的很多例子来看,CoT和最后的答案互相冲突,即standard CoT不能够解释LLM的思考过程。如:

那么最后这种错误的答案到底是如何得到的,实际上不能够用CoT来解释。
Solution: 作者提出了个两阶段的过程,第一个阶段将原来的自然语言NL问题转化为多个由符号语言描述的子问题,也就是reason chain;第二个阶段,调用外部工具来执行/解决reason chain。那么这样的话,第二个阶段,执行reason chain的过程是faithful的,人们能够明确的知道是什么样的推理过程导致了最终的answer;但是第一个过程不保证是faithful的。
第一个阶段将原来的NL question分为多个子问题,每个子问题被任务特定的符号语言SL来进行解决。由NL comments (\(C_{NL}\))和SL program (\(C_{SL}\))组成。 第二个阶段通过调研外部工具来执行对应子问题的program。
不同的task,作者设计了不同的prompt template,会调用不同的外部工具来解决:
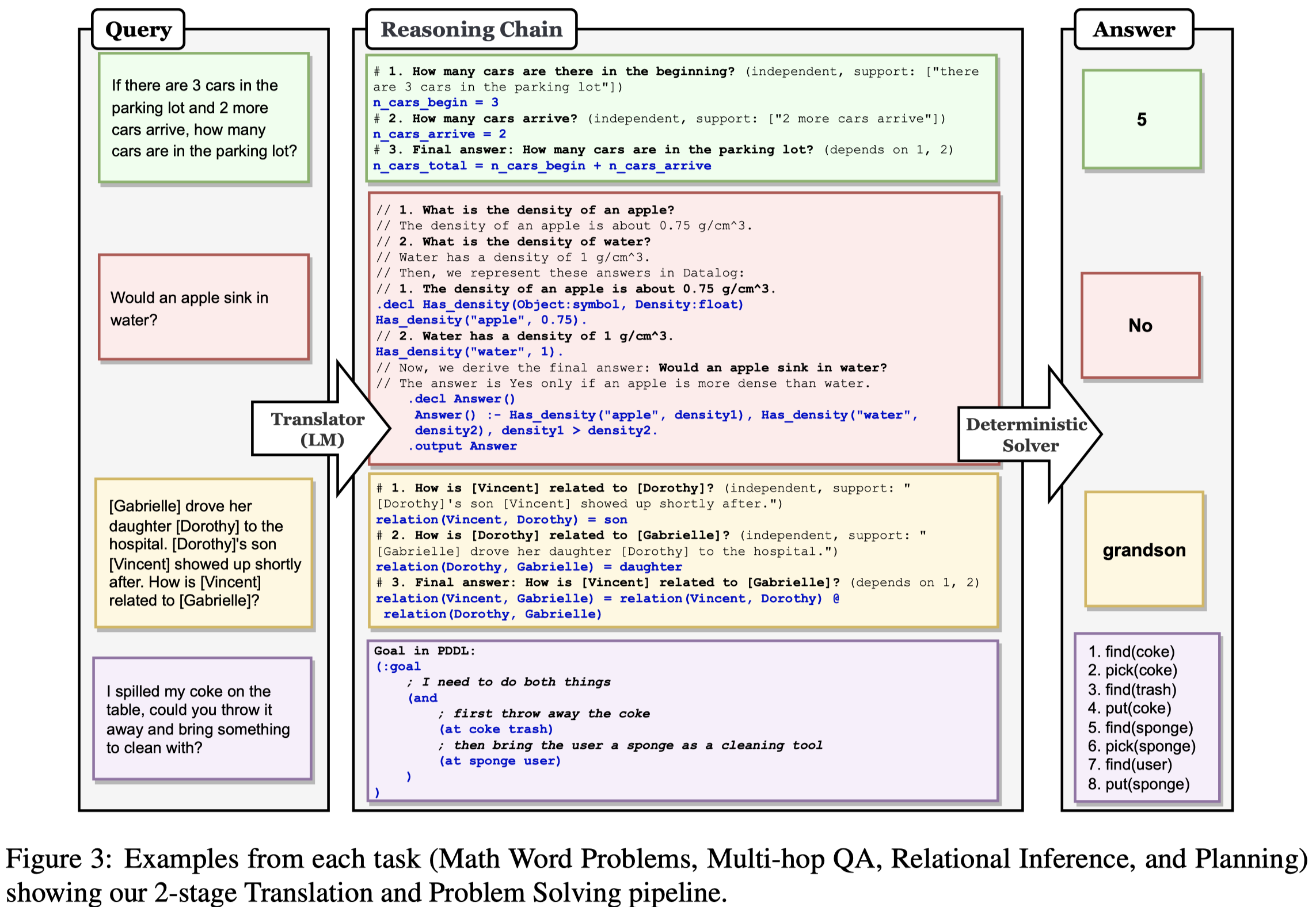
实验主要使用code-davinci-002,在Math Word Problems、Multi-hop QA、Planning、Relational inference上进行了实验。
PoT
Program of Thoughts Prompting: Disentangling Computation from Reasoning for Numerical Reasoning Tasks. University of Waterloo. TMLR 2023.
Recently, there has been significant progress in teaching language models to perform step-by-step reasoning to solve complex numerical reasoning tasks. Chain-of-thoughts prompting (CoT) is the state-of-art method for many of these tasks. CoT uses language models to produce text describing reasoning, and computation, and finally the answer to a question. Here we propose ‘Program of Thoughts’ (PoT), which uses language models (mainly Codex) to generate text and programming language statements, and finally an answer. In PoT, the computation can be delegated to a program interpreter, which is used to execute the generated program, thus decoupling complex computation from reasoning and language understanding. We evaluate PoT on five math word problem datasets and three financialQA datasets in both few-shot and zero-shot settings. We find that PoT has an average performance gain over CoT of around 12% across all datasets. By combining PoT with self-consistency decoding, we can achieve extremely strong performance on all the math datasets and financial datasets. All of our data and code will be released.
Issue: standard CoT中,LLM会同时负责reasoning和computation,作者认为LLM并不适合直接计算mathematical expressions:
- LLMs are very prone to arithmetic calculation errors, especially when dealing with large numbers; LLM对数据不敏感,常计算错误
- LLMs cannot solve complex mathematical expressions like polynomial equations or even differential equations; LLM无法解决复杂的数据公式
- LLMs are highly inefficient at expressing iteration, especially when the number of iteration steps is large. LLM无法很好的处理迭代
Solution: 作者提出,应该把计算过程从CoT中分离,让其它的外部工具如Python interpreter来解决。这一思想本质上,和前面提到的PAL、faithful CoT是一样的。
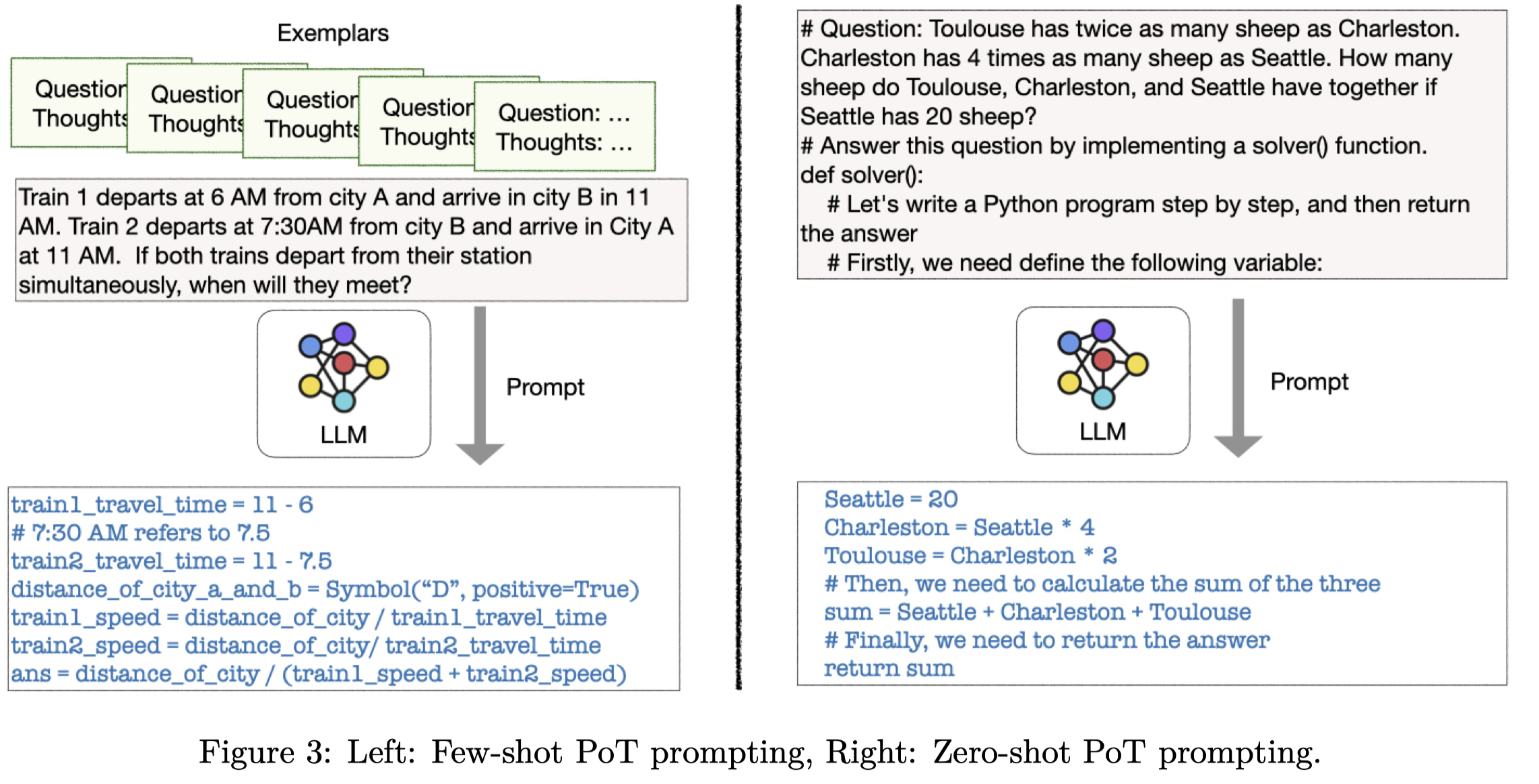
zero-shot PoT利用python comment来诱导LLM生成对应的代码,以及获得答案。和zero-shot CoT相比,可以直接一步获得reason chain以及answer。
PoT也可以作为pipline的中间步骤,再结合CoT来解决问题:
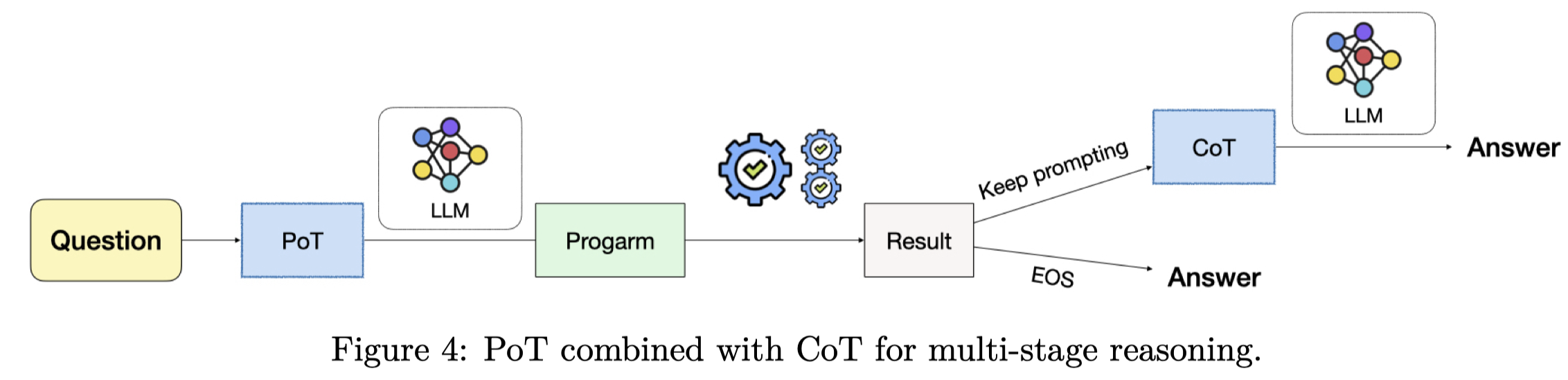
实验部分,作者主要使用code-davinci-002,但同时使用了text-davinci-002, gpt-turbo-3.5, codegen-16B, CodeT5+, Xgen用于消融实验。在在Math Word Problems,QA数据集上进行实验
SatLM
SatLM: Satisfiability-Aided Language Models Using Declarative Prompting. The University of Texas at Austin. NeurIPS 2023. 代码.
Prior work has combined chain-of-thought prompting in large language models (LLMs) with programmatic representations to perform effective and transparent reasoning. While such an approach works well for tasks that only require forward reasoning (e.g., straightforward arithmetic), it is less effective for constraint solving problems that require more sophisticated planning and search. In this paper, we propose a new satisfiability-aided language modeling (SatLM) approach for improving the reasoning capabilities of LLMs. We use an LLM to generate a declarative task specification rather than an imperative program and leverage an off-the-shelf automated theorem prover to derive the final answer. This approach has two key advantages. The declarative specification is closer to the problem description than the reasoning steps are, so the LLM can parse it out of the description more accurately. Furthermore, by offloading the actual reasoning task to an automated theorem prover, our approach can guarantee the correctness of the answer with respect to the parsed specification and avoid planning errors in the solving process. We evaluate SatLM on 8 different datasets and show that it consistently outperforms program-aided LMs in the imperative paradigm. In particular, SatLM outperforms program-aided LMs by 23% on a challenging subset of the GSM arithmetic reasoning dataset; SatLM also achieves a new SoTA on LSAT and BOARDGAMEQA, surpassing previous models that are trained on the respective training sets.
Issue:作者认为的解决复杂推理所需3步:
- parsing a natural language description into a representation of the problem
- deriving a plan to solve the problem
- executing that plan to obtain an answer.
PoT、faithful CoT等方法通过修复execution error来提高推理性能。将CoT表示为program,意味着推理的顺序,就是执行的顺序。这种做法适合于原始question已经隐含了某种解决问题的plan。但是对于解决更加复杂的问题没有帮助,比如存在很多premises,要求能够进行演绎推理,求满足约束的答案的任务。
Solution: 作者的方法,LLM只负责理解question中的各种状态、约束等,然后负责将自然语言NL question转化为逻辑表达式。具体求解通过调用外部solver来解决。

作者认为将推理过程表示为program,属于是命令式。在这篇论文中,作者提出使用声明Declarative的方法。和之前的PoT等program CoT方法比较,作者的方法让LLM进一步只关注如何理解问题即可:
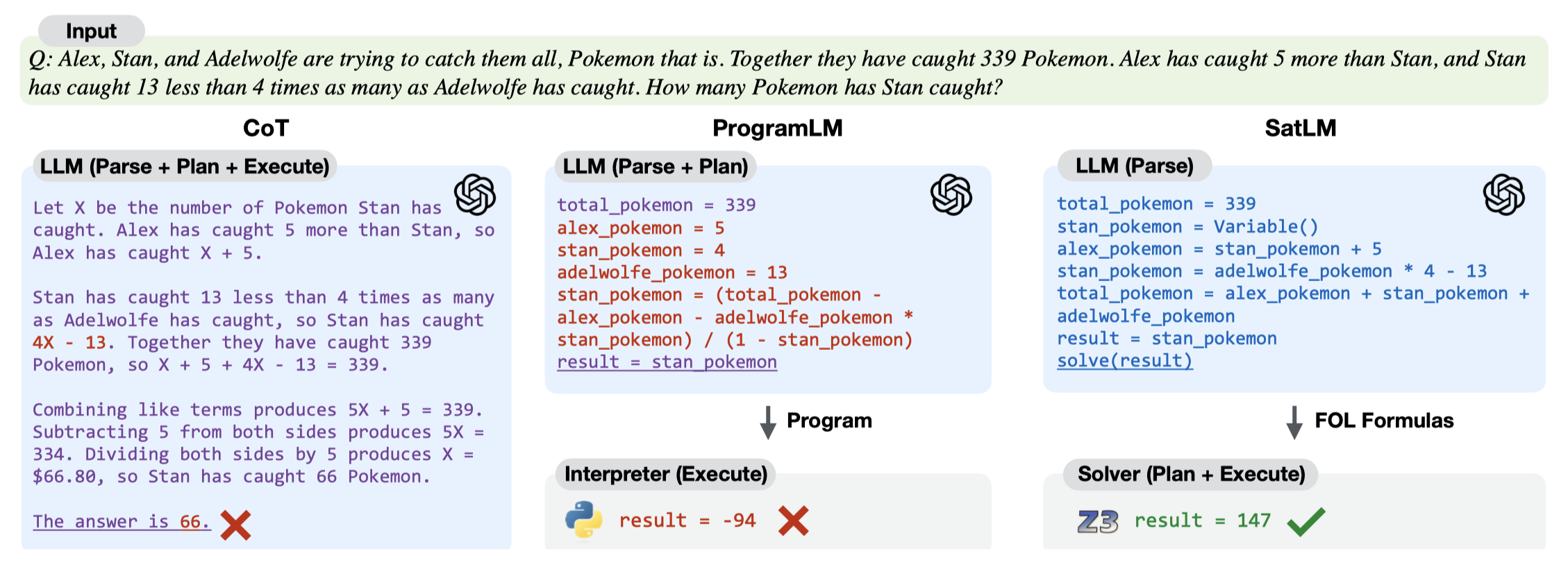
作者人工为几个样例写出对应的SAT问题(SATisfiability problem),然后作为demonstrations,让LLM将原始问题转化为SAT问题。作者定义的SAT问题是\(P=\{ \Phi, \mathcal{T},Q \}\),其中的\(\Phi\)表示set of first-order logic formulas;\(\mathcal{T}\)表示the meaning of some of the symbols used in the formula;\(Q\)表示query。一个简单的SAT实例:

之后调用外部的推理工具来解决该问题,any automated reasoning tool for checking the satisfiability of formulas in formal logic.
利用这种外部solver比单纯的program的好处之一是,它可以返回更多的错误信息,比如存在互相冲突的条件unsatisfiable formulas (UNSAT)、存在多种可行解ambiguous formulas (AMBIG)等。
作者实验基于code-davinci-002,在arithmetic reasoning和logical reasoning tasks任务上进行了实验。
HiT
Large Language Models can Learn Rules. Google DeepMind. arXiv 2023.10.
When prompted with a few examples and intermediate steps, large language models (LLMs) have demonstrated impressive performance in various reasoning tasks. However, prompting methods that rely on implicit knowledge in an LLM often hallucinate incorrect answers when the implicit knowledge is wrong or inconsistent with the task. To tackle this problem, we present Hypotheses-to-Theories (HtT), a framework that learns a rule library for reasoning with LLMs. HtT contains two stages, an induction stage and a deduction stage. In the induction stage, an LLM is first asked to generate and verify rules over a set of training examples. Rules that appear and lead to correct answers sufficiently often are collected to form a rule library. In the deduction stage, the LLM is then prompted to employ the learned rule library to perform reasoning to answer test questions. Experiments on both numerical reasoning and relational reasoning problems show that HtT improves existing prompting methods, with an absolute gain of 11-27% in accuracy. The learned rules are also transferable to different models and to different forms of the same problem.
Issue:当LLM面临的task和常见的设置/knowledge不同的时候,LLM的表现很差。LLM的幻觉,特别是在面对不常出现的knowledge,或者和real life冲突的情况下更加明显。作者认为这是因为LLM的implicit knowledge和task required knowledge之间的gap引起的。
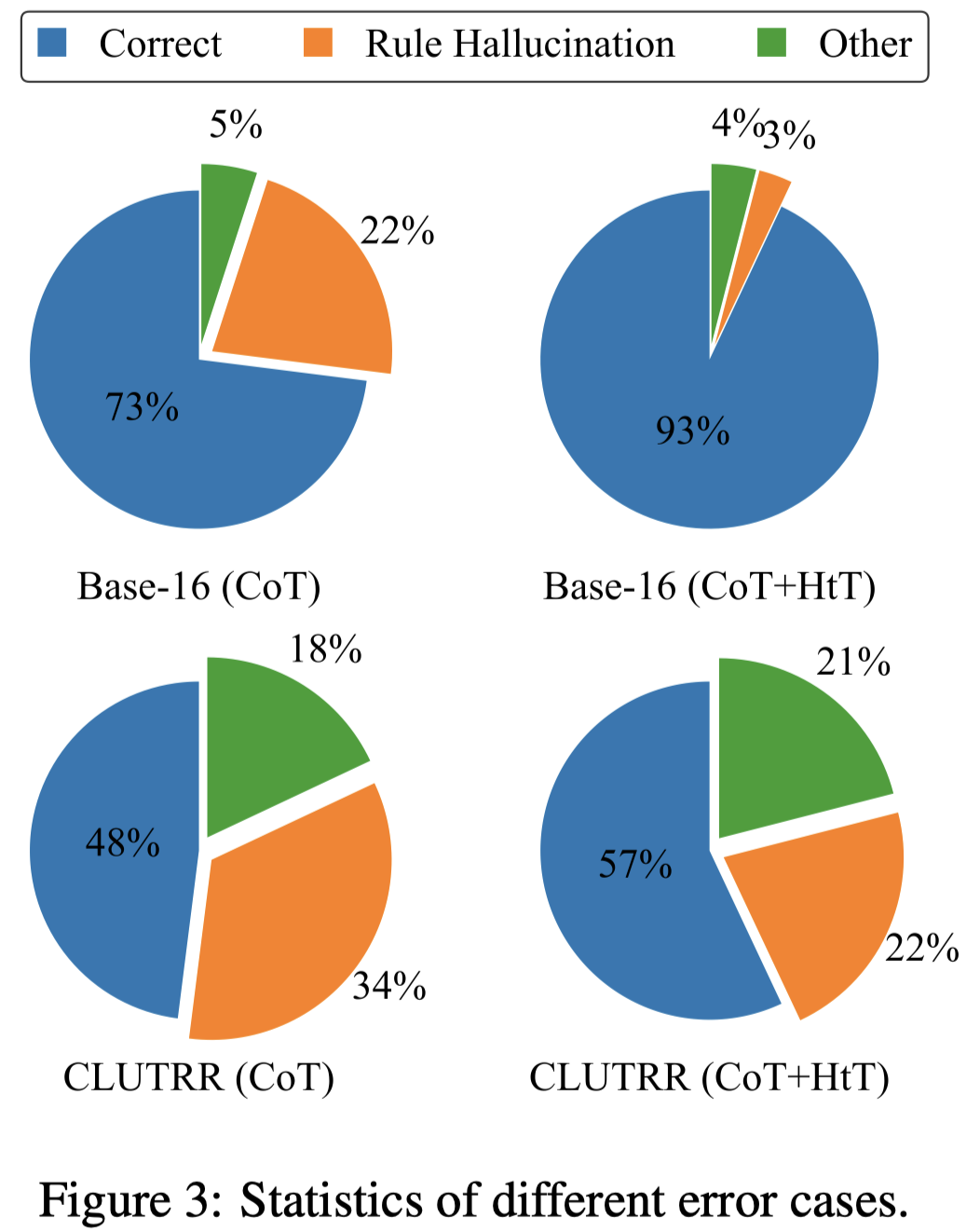
作者的推理实验中发现,CoT方法出错中,有60%以上的原因是因为它自认为的rule是错误的
A manual analysis indicates that rule hallucination constitutes 81% and 65% of the errors made by CoT on base-16 Arithmetic and CLUTRR respectively (Figure 3).
Solution:从现有的训练数据中,总结归纳explicit knowledge,即rules。
作者将LLM的推理过程,和scientific theories发现的过程联系到一起
the process of scientific discovery starts by allowing humans to freely “hallucinate” hypotheses, but theories are only kept if they are verified by experiments.
大多数LLM的prompting方法,例如CoT可以看做是演绎推理,利用LLM内在的implicit rules+given facts,来deduce conclusions。
作者的方法图:

第一步归纳rule的时候,需要归纳并且验证两步。最后选择
Specifically, we collect the rules generated by the LLM over the entire training set, and only keep those that appear more than \(k\) times and pass the verification test with a probability higher than \(p\).
但是,考虑到两步操作会增加prompt engineering effort,所以作者直接在一步prompting内,让LLM在预测过程中生成新rule,并且利用rule进行预测。从LLM deduction过程中,提取rules。
在第二步进行演绎的时候,也就是如何利用rule来执行任务。作者发现如果给LLM很多rule,则LLM并不擅长找到合适的rule。因此作者利用XML来认为定义了rule的层级,把相似的rule放在一组;然后每次可以只检索返回少数的rules,这样模型就能够比较好的利用rule来进行推测。

作者实验基于gpt-3.5-turbo和gpt-4。在relational reasoning和numerical reasoning两个任务上进行了实验。

LINC
LINC: A Neurosymbolic Approach for Logical Reasoning by Combining Language Models with First-Order Logic Provers. EMNLP 2023. MIT. 代码.
Logical reasoning, i.e., deductively inferring the truth value of a conclusion from a set of premises, is an important task for artificial intelligence with wide potential impacts on science, mathematics, and society. While many prompting-based strategies have been proposed to enable Large Language Models (LLMs) to do such reasoning more effectively, they still appear unsatisfactory, often failing in subtle and unpredictable ways. In this work, we investigate the validity of instead reformulating such tasks as modular neurosymbolic programming, which we call LINC: Logical Inference via Neurosymbolic Computation. In LINC, the LLM acts as a semantic parser, translating premises and conclusions from natural language to expressions in first-order logic. These expressions are then offloaded to an external theorem prover, which symbolically performs deductive inference. Leveraging this approach, we observe significant performance gains on FOLIO and a balanced subset of ProofWriter for three different models in nearly all experimental conditions we evaluate. On ProofWriter, augmenting the comparatively small open-source StarCoder+ (15.5B parameters) with LINC even outperforms GPT-3.5 and GPT-4 with Chain-of-Thought (CoT) prompting by an absolute 38% and 10%, respectively. When used with GPT-4, LINC scores 26% higher than CoT on ProofWriter while performing comparatively on FOLIO. Further analysis reveals that although both methods on average succeed roughly equally often on this dataset, they exhibit distinct and complementary failure modes. We thus provide promising evidence for how logical reasoning over natural language can be tackled through jointly leveraging LLMs alongside symbolic provers. All corresponding code is publicly available.
Issue: 作者认为现在LLM的推理方法面对unreliable for tasks that require reasoning out of domain (Liang et al., 2022; Saparov et al., 2023), understanding negation (Anil et al., 2022), and following long reasoning chains (Dziri et al., 2023)等场景时存在问题。这表明了LLM可能是依赖于surface-level的statistical patterns来进行推理,而不是依赖于更加generalizable和consistent的表示来推理:
These findings suggest that such models may be relying on approximate heuristics based on surface-level statistical patterns in reasoning tasks, rather than consistent, generalizable representations and strategies (Srivastava et al., 2023; Creswell et al., 2023).
Solution:为了使得LLM成为更加reliable logical reasoner,作者结合外部符号系统,让LLM只是单纯的作为semantic parser,负责将原来自然语言描述的premise和conclusion转化为一阶逻辑,然后利用外部的prover来判断conclusion是否正确:
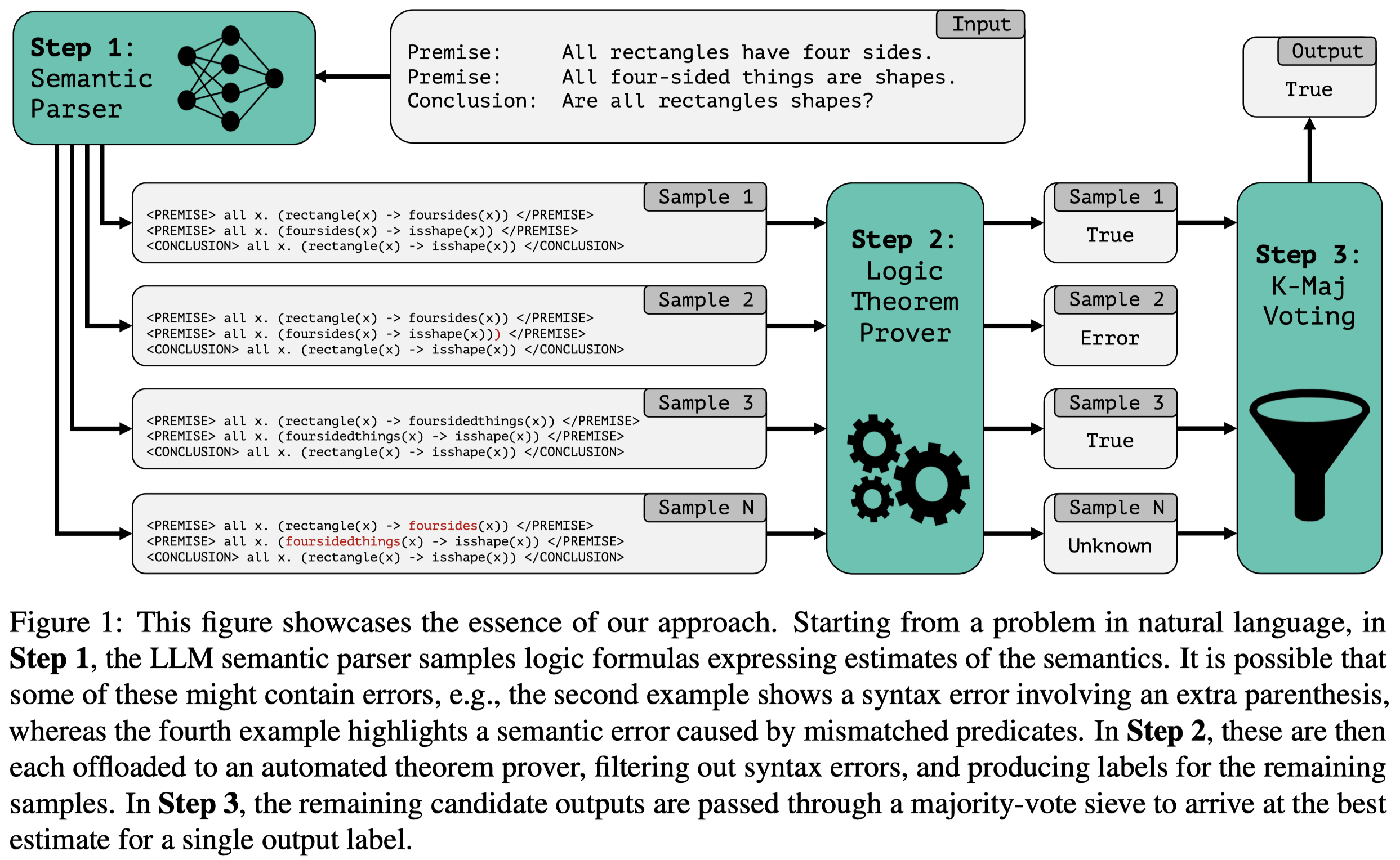
外部的prover作者使用的是Prover9, a high-performance prover widely used in the logic community (McCune, 2005–2010). 它能够判断conclusion的结果:\(\{True, False, Uncertain\}\)或者是syntax错误的报告。
利用外部prover的好处就是能够保证推理结果和premises是一致的,deductive chains will be correct with respect to the semantics of the intermediate representation。
作者实验在FOLIO和ProofWriter两个数据集上进行。

作者关于CoT推理结果的一些发现:
- CoT concludes something different than it suggests
- CoT makes incorrect logical deductions:错误的logical deduction,例如“if \(B\) is true and \(A \rightarrow B\), then \(A\) is true”
- CoT fails to find complex paths of reasoning:复杂推理时中间过程出错,或者干脆开始时就失败
LOIRE
Can LLMs Reason with Rules? Logic Scaffolding for Stress-Testing and Improving LLMs. 复旦. arXiv. 代码.
impressive human-like performance across various reasoning tasks. However, their mastery of underlying inferential rules still falls short of human capabilities. To investigate this, we propose a logic scaffolding inferential rule generation framework, to construct an inferential rule base, ULogic, comprising both primitive and compositional rules across five domains. Our analysis of GPT-series models over a rule subset reveals significant gaps in LLMs’ logic understanding compared to human performance, especially in compositional and structural complex rules with certain bias patterns. We further distill these rules into a smaller-scale inference engine for flexible rule generation and enhancing downstream reasoning. Through a multijudger evaluation, our inference engine proves effective in generating accurate, complex and abstract conclusions and premises, and improve various commonsense reasoning tasks. Overall, our work sheds light on LLMs’ limitations in grasping inferential rule and suggests ways to enhance their logical reasoning abilities.
Issue:LLM到底是否能够像人一样捕获问题underlying logic?
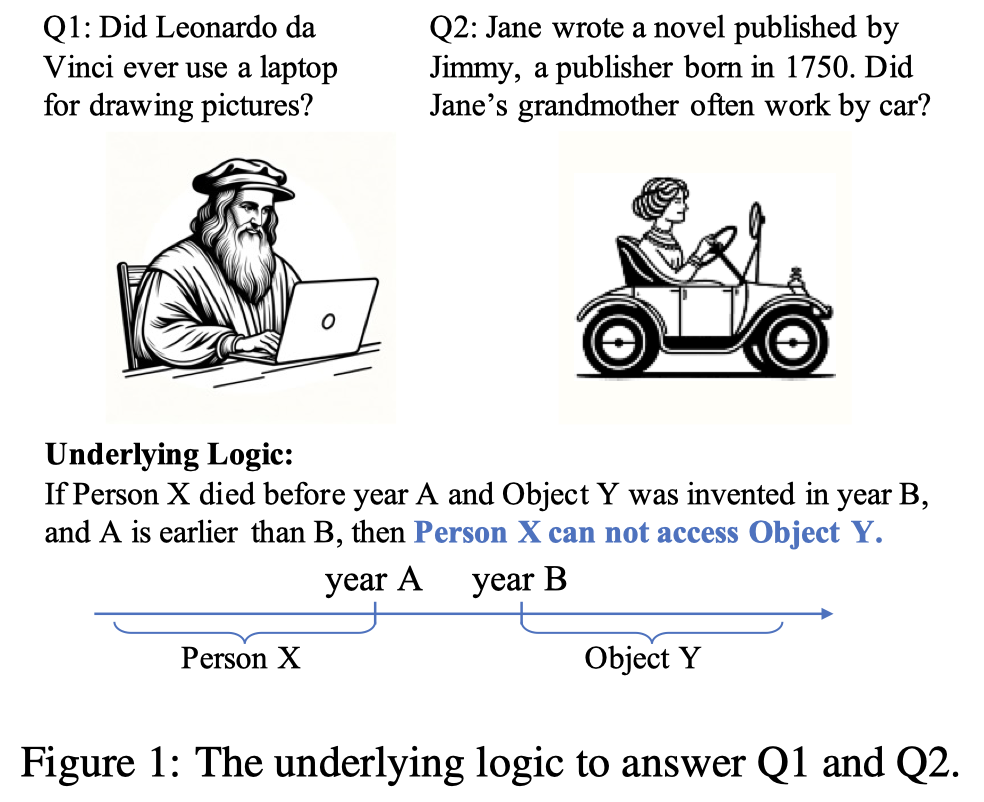
人们常常能够从大量的real world observations中抽取出logics,比如inferential rules:
An inferential rule is typically defined as a premise with a set of facts (e.g., “Person X died before ... earlier than B”) leading to a conclusion (e.g., ‘‘Person X cannot access Object Y”) (Boghossian, 2014).
为了评估大模型的推理演绎推理能力,首先需要收集大量的rules。创造这样的rules需要大量的人工,并且人工创造的rules常常是simple,只包含很少的premise,并且覆盖的范围也没法保证。
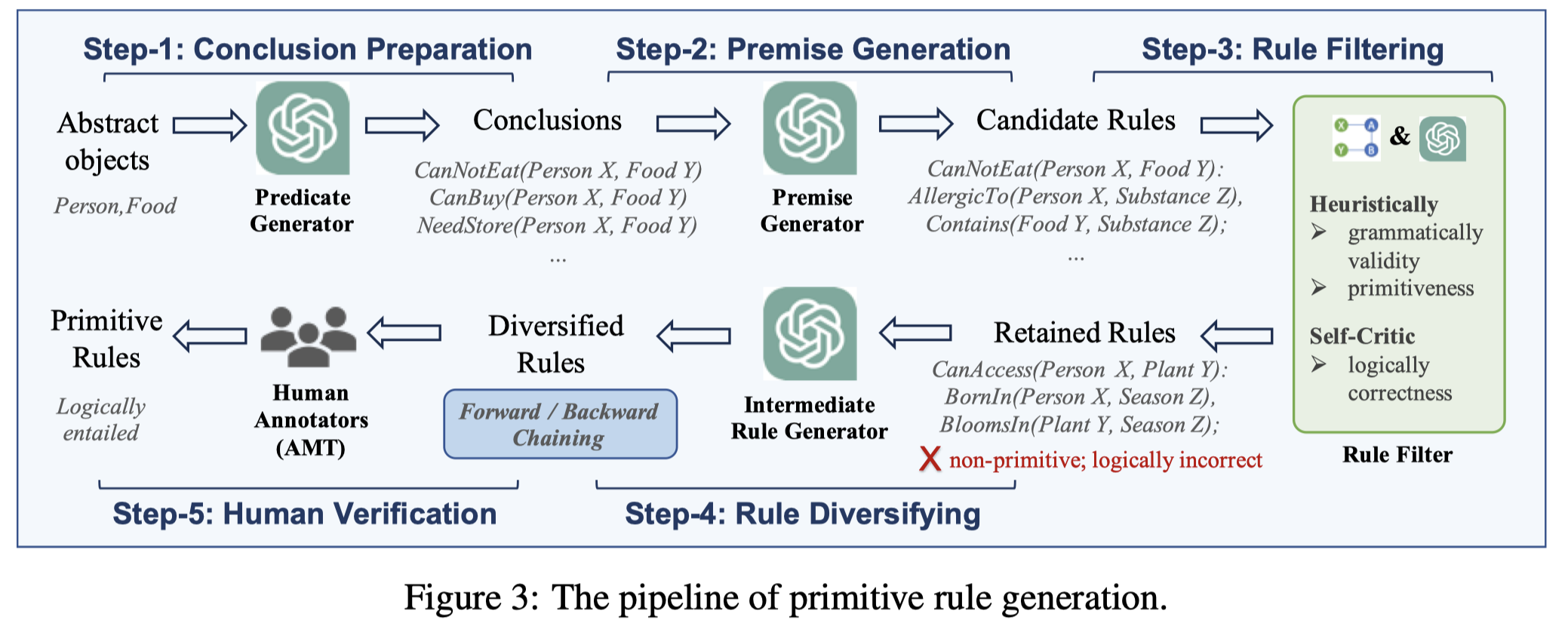
Solution:作者构造了一个pipeline Logic scaffOlding Inferential Rule gEneration (LOIRE)来创造数据集ULogic:
作者使用的Inferential Rules:
we focus on if-then inferential rules with variables, that can be easily expressed as symbolic logic (Novák and Lehmke, 2006).
An inferential rule describes a logical implication from a premise (a set of facts) to a conclusion (a specific fact), where each fact is a predicate expression with two variables, and each variable has a designated variable type.
作者使用Prolog (Apt et al., 1997)来formulate对应的rules:
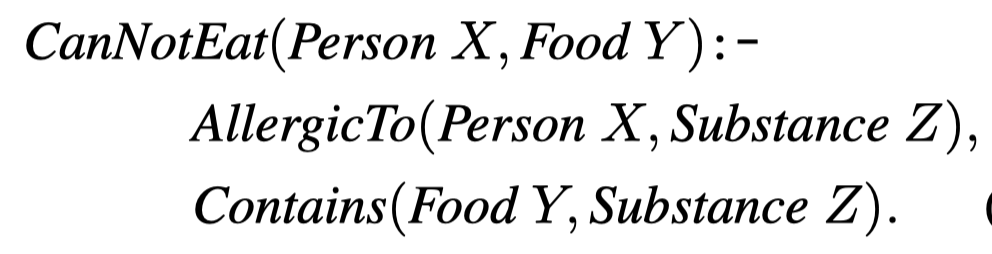
其对应的verbalized forms:
If Person X is allergic to Substance Z and Food Y contains Substance Z, then Person X cannot eat Food Y.
不同推理路径类型的rules:

步骤:
Conclusion Preparation:作者人工从ConceptNet和WordNet中选择abstract objects和它们对应的common properties。然后选择两个type的objects,让LLM从5个domain {object affordance, accessibility, interaction, location and person’s need}中生成可能链接这两个objects的predicates,作为conclusion。


Premise Generation: 利用GPT-4,为conclusion生成premises in both symbolic and verbalized forms
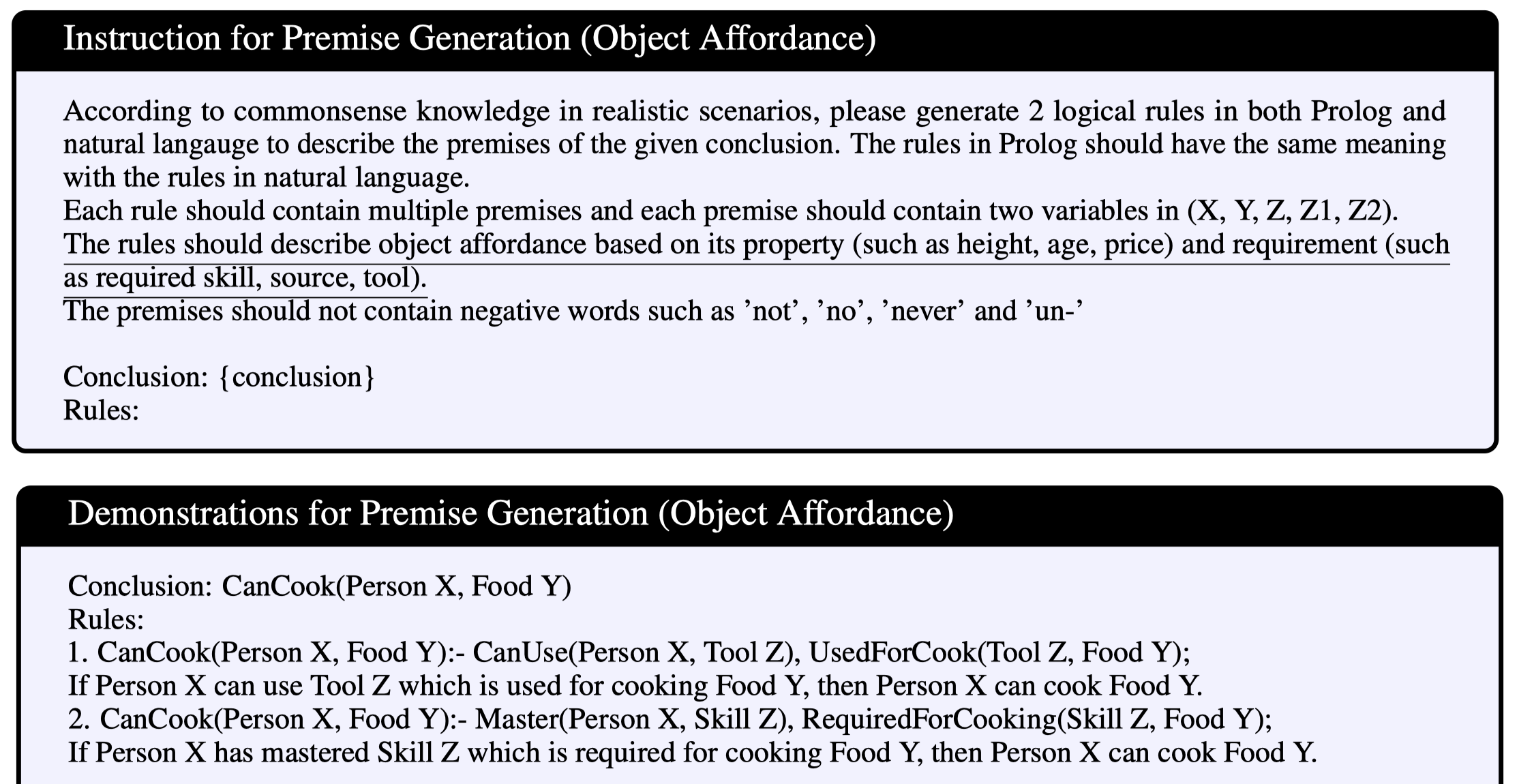
Rule Filtering:根据premise的symbolic form过滤掉语法错误的rule;然后self-critic策略,LLM评估自己生成的结果

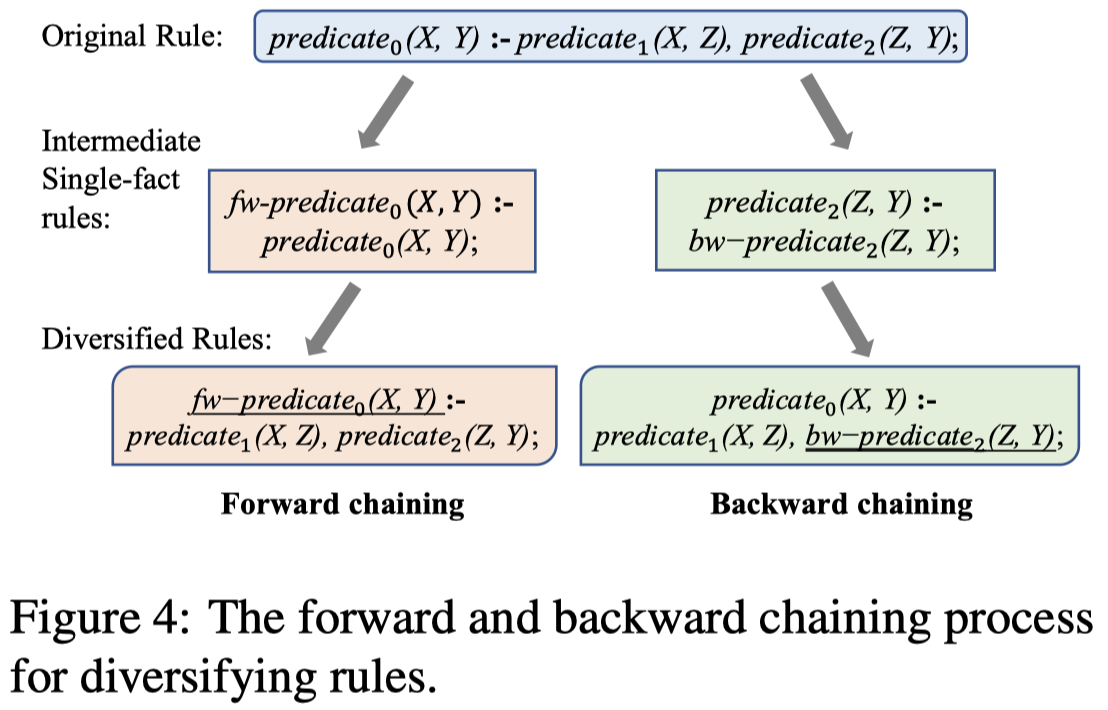
Rule Diversifying:增加生成的rule的多样性。
- forward chaining:conclusion fact作为input,生成新的conclusion,替换
- backward chaining:a premise作为input,生成新的premise,替换
Human Verification:Amazon Mechanical Turk (AMT)进行人类评估
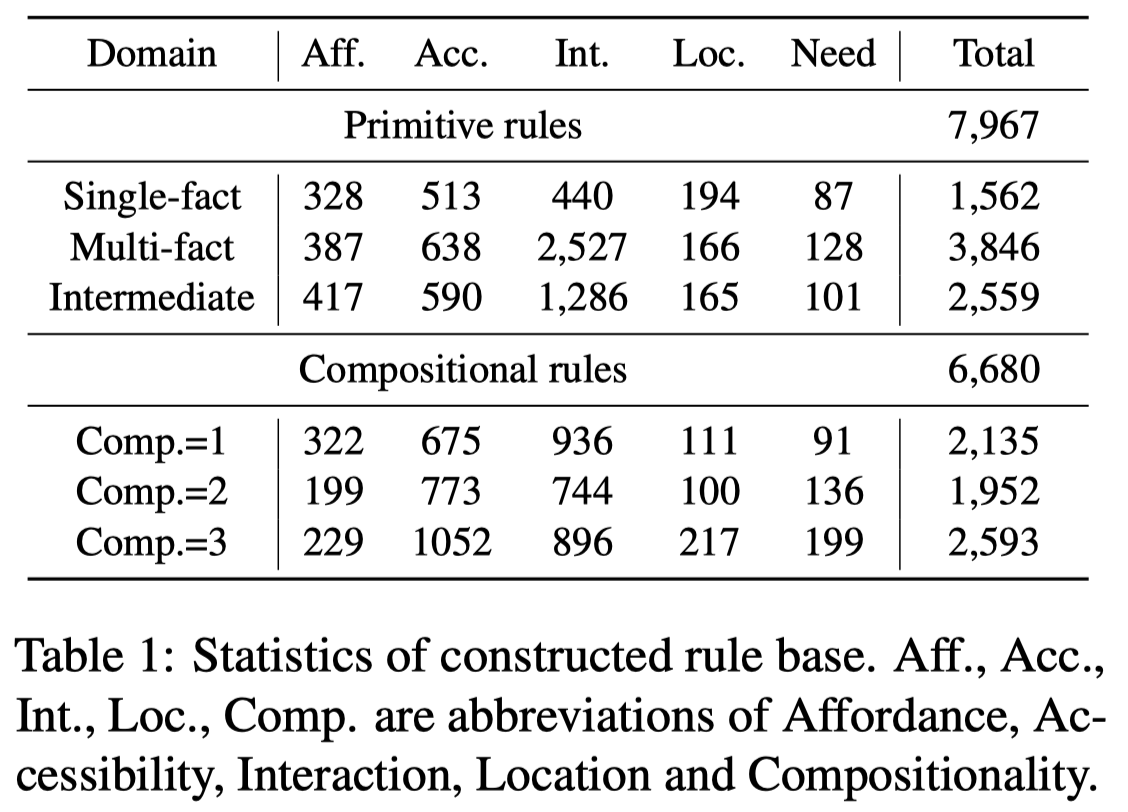
前面生成的是primitive rules,作者进一步生成组合的rule。通过不同次数的backward chaining,就可以逐步的生成更加复杂的premise。构造的数据集统计:
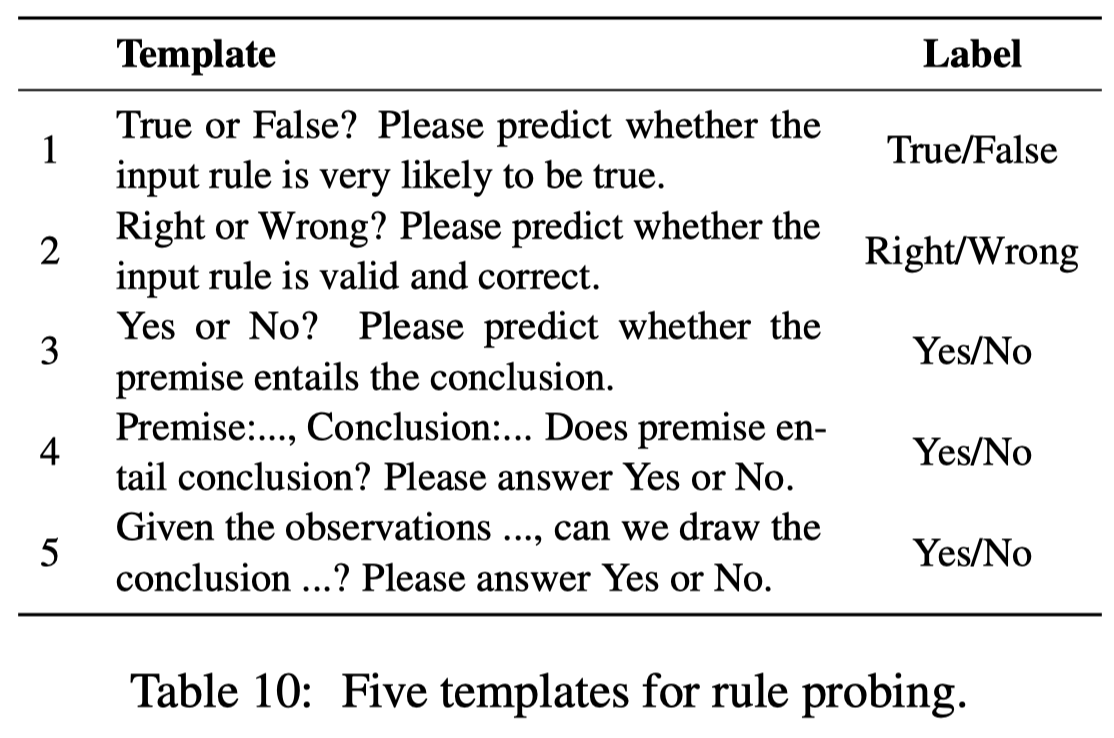
作者的实验就是基于构造的Ulogic,来判断LLM是否能够较好的进行规则推理。每个测试的rule,被转化为下面的5种二分类template:
一个rule是否能够被LLM正确推理,要求让LLM即判断conclusion要成立,同时要判断negative conclusion不成立:

一些实验发现:
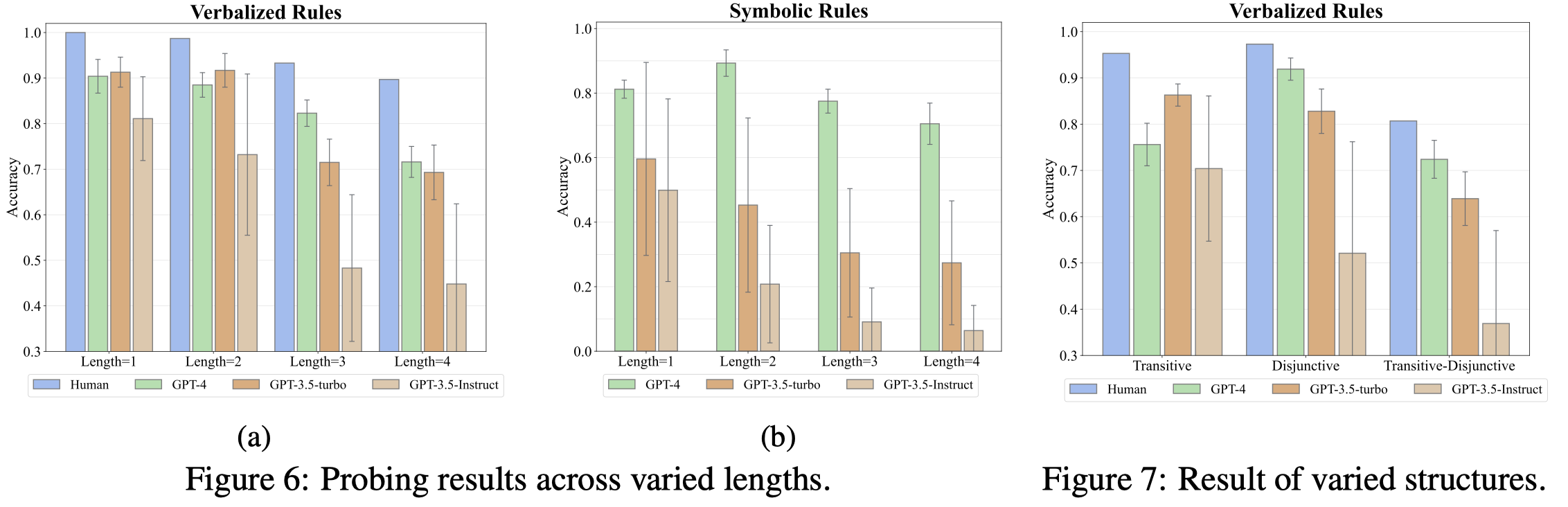
- 越复杂的规则,LLM越难以正常推理;同时和人类有差距
- 对于transitive rules,GPT-4反而是更加谨慎地判断,存在necessary bias要考虑所有必要的情况都成立。这造成了其对于transitive类型rule的判断效果下降:

- GPT-3.5对于symbolic rule的理解能力并不好;也就是说symbolic rule的理解,不是所有LLM都能够比较好的学习好的
最后,作者还尝试了把rule生成的能力蒸馏给更小的LLM Mistral 7b,使用\(10,703\)个rules生成了\(39,887\)训练样本:\(10,703\), \(18,500\) and \(10,684\) for conclusion generation, premise completion and premise generation。使用Quantization LoRA微调。
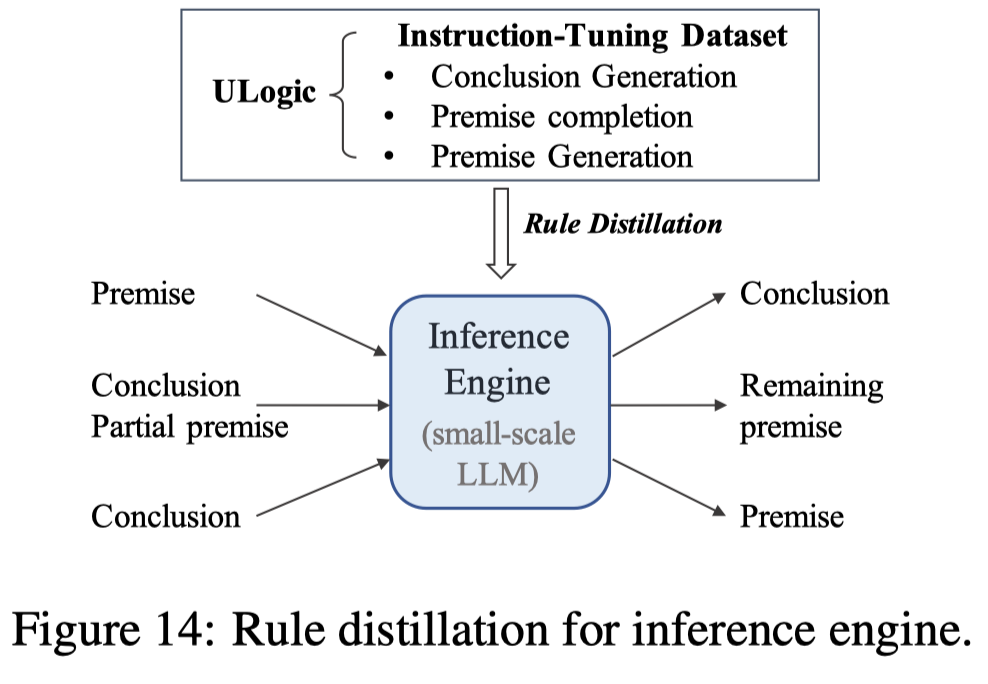
蒸馏的效果,人工评估要好于GPT-3.5:
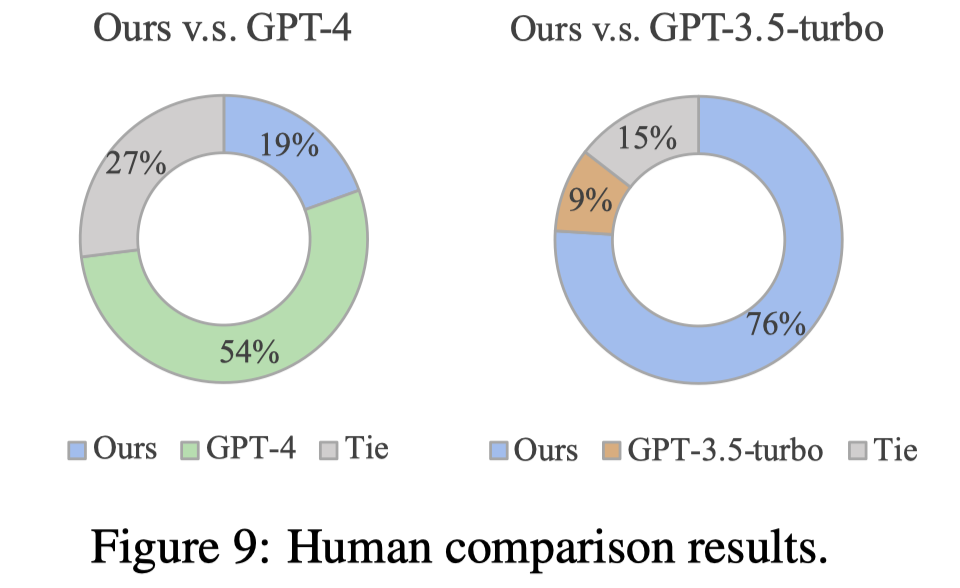
作者还尝试了把蒸馏的小LM用于下游任务,具体做法是利用其来为问题生成rules或者explanations,作为rationales加入到demonstrations中。
ChatRule
ChatRule: Mining Logical Rules with Large Language Models for Knowledge Graph Reasoning. Monash University. arXiv 2024. 代码.
Logical rules are essential for uncovering the logical connections between relations, which could improve reasoning performance and provide interpretable results on knowledge graphs (KGs). Although there have been many efforts to mine meaningful logical rules over KGs, existing methods suffer from computationally intensive searches over the rule space and a lack of scalability for largescale KGs. Besides, they often ignore the semantics of relations which is crucial for uncovering logical connections. Recently, large language models (LLMs) have shown impressive performance in the field of natural language processing and various applications, owing to their emergent ability and generalizability. In this paper, we propose a novel framework, ChatRule, unleashing the power of large language models for mining logical rules over knowledge graphs. Specifically, the framework is initiated with an LLM-based rule generator, leveraging both the semantic and structural information of KGs to prompt LLMs to generate logical rules. To refine the generated rules, a rule ranking module estimates the rule quality by incorporating facts from existing KGs. Last, the ranked rules can be used to conduct reasoning over KGs. ChatRule is evaluated on four large-scale KGs, w.r.t. different rule quality metrics and downstream tasks, showing the effectiveness and scalability of our method.
Issue: LLM有很多的常识适合于KG reasoning,但是LLM本身并不理解KG的结构。
Solution: 作者的方法主要是,通过采样现有KG中的paths构造rules,然后利用LLM来生成更多rules。为了判断LLM生成的rules是否成立,作者从多个统计metric来选择可信rules。
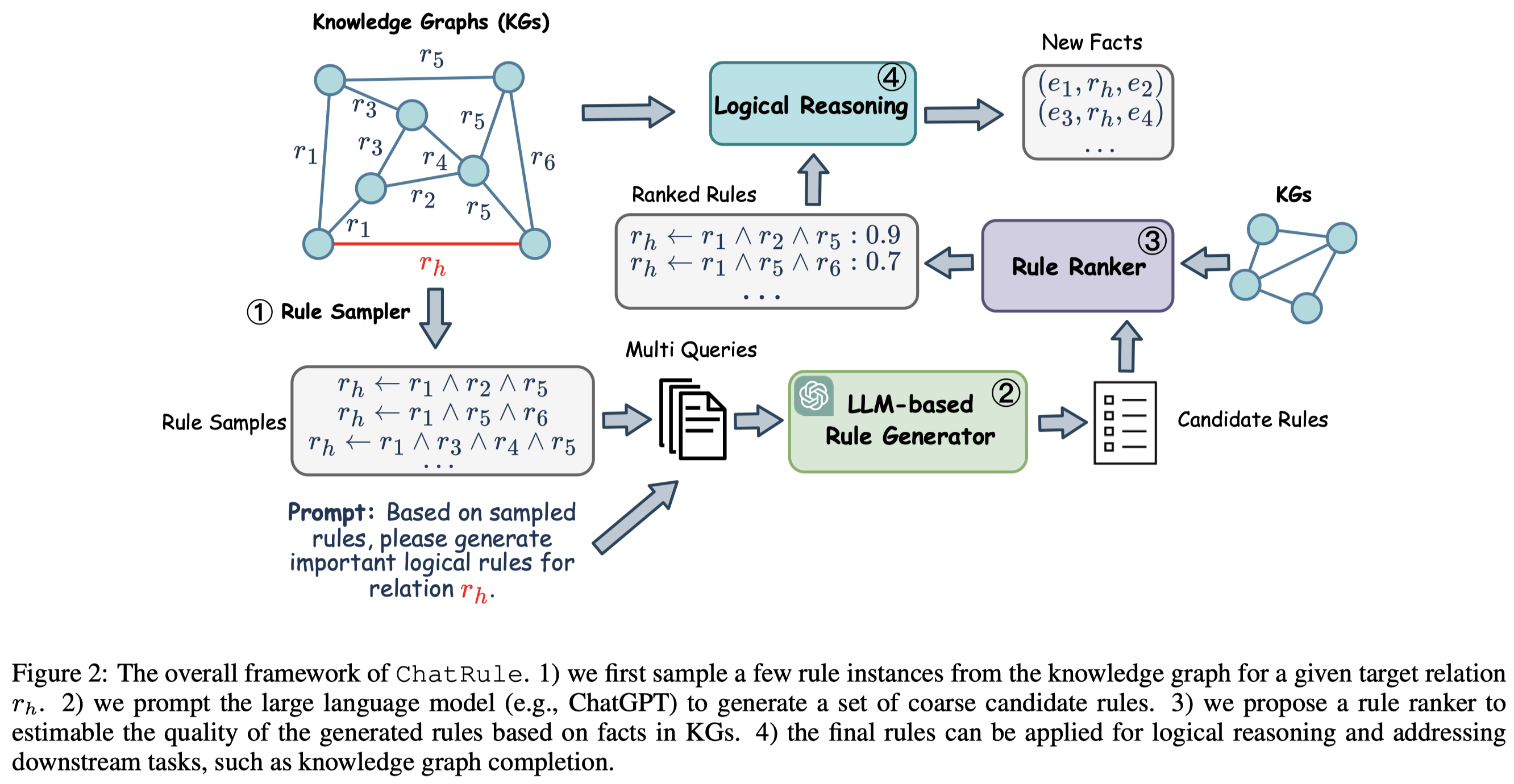
KG中的logical rules定义,包括body和head。body的长度就是rule的长度:
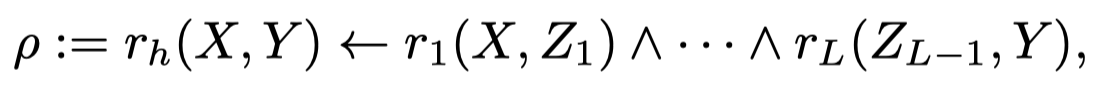
先利用广度优先搜索BFS采样KG中的closed-paths,也就是说在KG中存在的三元组\((e_1,r, e_2)\),寻找从\(e_1\)出发能够抵达\(e_2\)的path。然后把具体的中间实体去掉,只保留relation,就得到了候选rules。
然后用自然语言形式描述rules,让LLM生成更多的rules:

为了评估rule的可信程度,作者从Support、Coverage、Confidence、PCA Confidence几个metric进行评估。
随后,选择可信的rules,直接进行KG推理。